Тема: «Функция 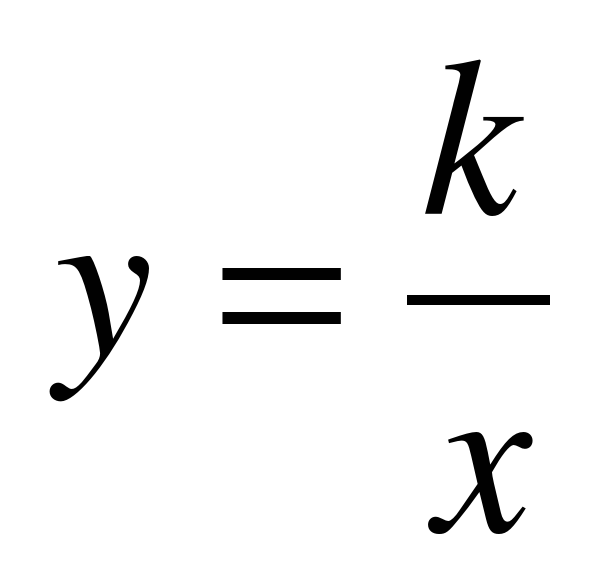 и ее график».
и ее график».
Цели:
Сформулировать определение обратной пропорциональности, научить находить значение функции и аргумента по формуле 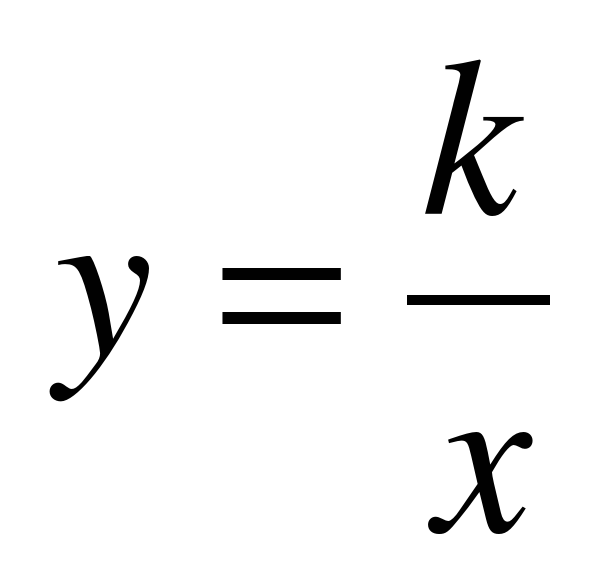 , способствовать выработке навыков и умений в построении графика функции вида
, способствовать выработке навыков и умений в построении графика функции вида 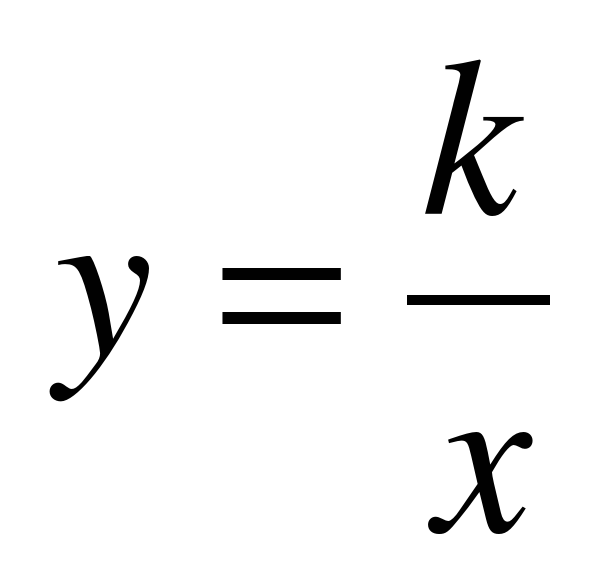 .
.
Способствовать формированию информационной компетентности: умения систематизировать, анализировать, сравнивать, делать выводы.
Воспитание ответственного отношения к учебному труду.
Тип урока: урок изучения нового материала.
Оборудование:
Компьютер, проектор;
Презентация урока (PowerPoint);
Карточки с заданием для самостоятельной работы.
Оборудование доски:
Таблицы 1, 2.
Структура урока:
Постановка цели урока (2 мин);
Подготовка к изучению нового материала и ознакомление с ним (20 мин).
Физкультминутка (3 мин),
Первичное осмысление и применение изученного (8 мин).
Самостоятельная работа (7 мин).
Постановка домашнего задания (2 мин).
Подведение итогов урока(3 мин).
Ход урока.
Постановка цели урока.
Проверяется подготовленность классного помещения и готовность учащихся к уроку.
Отмечается, что продолжается изучение темы «Функция». Сегодня мы рассмотрим новый тип функции – обратную пропорциональность. На доске и в тетрадях учащихся записывается тема урока: «Функция 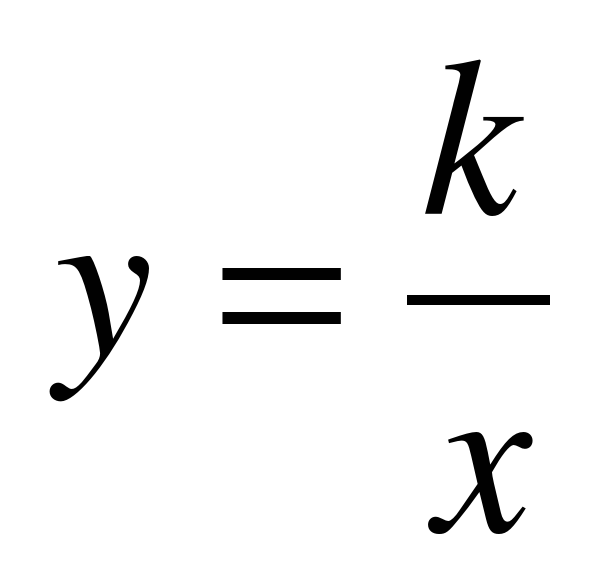 и ее график».
и ее график».
Подготовка к изучению нового материала.
В ходе фронтального опроса повторяются основные понятия по теме «Функция». Для этого учащимся предлагается разгадать кроссворд (Приложение 1). Вопросы кроссворда читает учитель. Шаблон кроссворда проецируются с помощью проектора на экран. Учащиеся устно последовательно отвечают на поставленные вопросы, а учитель в режиме презентации (PowerPoint) с помощью эффекта анимации вводит с помощью клавиатуры по очереди ответы в заготовленный шаблон кроссворда.
3. Ознакомление с новым материалом.
Ознакомление с новым материалом учитель осуществляет постепенно, поэтапно, опираясь на ранее полученные знания и умения учащихся.
Учитель задает вопросы, а учащиеся отвечают
Учитель: Какие способы задания функций нам известны?
Ученик: С помощью формулы, графика или таблицы.
Учитель предлагает двум ученикам, используя формулу 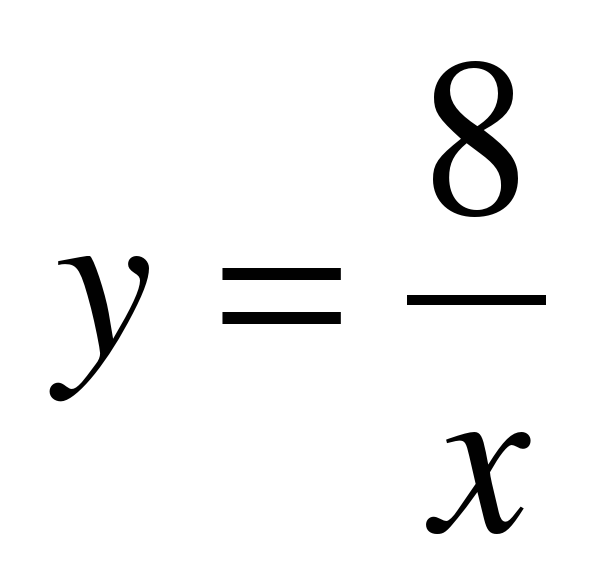 . заполнить заранее заготовленные на доске таблицы 1 и 2.
. заполнить заранее заготовленные на доске таблицы 1 и 2.
Таблица 1: Таблица 2:
Тем временем класс отвечает на вопросы учителя, которые проецируются на экран с помощью проектора.
Вопросы.
Как называются следующие функции, заданные формулами: y = kx + b,
y = x2 , y = kx2 , y = kx. (линейная функция, квадратичная функция, прямая пропорциональность)
Что означает термин «прямая пропорциональность»?
Какова область определения каждой из данных функций?
После фронтального разбора вопросов учащиеся проверяют правильность заполнения учениками таблиц 1 и 2.
Следующий ученик выполняет на доске новое задание: «По данным в таблицах 1, 2 значениям x и y построить в координатной плоскости соответствующие точки».
А в это время учитель проводит фронтальный опрос класса по таблице 3, которая проецируется на экран с помощью проектора.
Таблица 3.
| 1    y y
0 1 x | 2 y   
0 1 x | 3   y y 
1 x | 4  y y
0 1 x
|
| 5   y y
0 1 x | 6    y y
0 1 x | 7    y y
0 1 x | 8  y y
 0 1 x 0 1 x |
| 9 y y
  0 1 x 0 1 x | 1   0 y 0 y
 0 1 x 0 1 x | 1   1 y 1 y
 0 1 x 0 1 x | 1   2 y 2 y
 0 1 x 0 1 x
|
Вопросы:
На каком рисунке из таблицы изображен график
а) линейной функции;
б) прямой пропорциональности;
в) квадратичной функции;
г) функции вида y = kx3.
Назовите номера графиков функций вида y = kx + b, для которых k 0.
Найдите в таблице графики линейных функций, у которых угловые коэффициенты:
а) равны;
б) равны по модулю и противоположны по знаку.
Затем весь класс проверяет, верно ли ученик расставил точки на координатной плоскости.
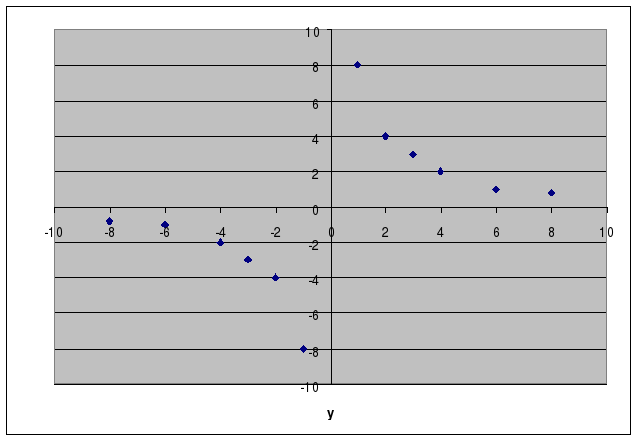
Учитель: Множество точек, изображенных на координатной плоскости образует график некоторой функции. Какой же формулой задается эта функция и как называется ее график?
Известно, всякая функция описывает какие-то процессы, происходящие в окружающем нас мире. Рассмотрим, например прямоугольник со сторонами x и y и площадью 8 см2. Тогда зависимость y от x будет выражаться формулой y = .
Что происходит со значениями y при увеличении (уменьшении) x в 2 раза, 4 раза? В какой зависимости находятся переменные y и x?
Ученик: В обратно - пропорциональной зависимости.
Учитель: В данной задаче переменные x и y принимали лишь положительные значения, а в дальнейшем мы будем рассматривать функции, задаваемые формулой y = , в которой переменные x и y могут принимать как положительные, так и отрицательные значения. Как будем называть такие функции?
Учащиеся формируют определение обратной пропорциональности, затем читают это определение по учебнику.
Учитель: Как же выглядит график обратной пропорциональности? По построенным точкам трудно судить обо всем графике. Попробуем вместе сделать выводы о графике данной функции, ответив на следующие вопросы.
Вопросы.
Какова область определения функции y = ?
Если x 0, то y 0?
x 0, то y ?
Пересекает ли график оси Ox и Oy, почему?
Выводы.
График находится в 1 и 3 координатных четвертях.
Плавно приближается к координатным осям, но не пересекает их.
Затем учитель соединяет точки и сообщает, что полученная кривая называется
гиперболой. Гипербола состоит из двух ветвей.
На этом этапе урока полезно сделать физкультминутку.
Первичное осмысление и применение изученного.
Оно начинается с выполнения следующего задания.
Задание: Построить график функции y = .
Один ученик выполняет на доске, учащиеся в тетрадях.
Учитель: Как зависит расположение графика гиперболы y = от значения k?
Ученик: Если k 0, то график расположен в 1 и 3 координатных четвертях.
Если k
Закрепление: Все учащиеся выполняют из учебника № 175, 177. Двое учащихся работают на боковой доске. По окончании работы проверяется правильность решения заданий.
Для более четкого представления о степени усвоения нового материала, учитель предлагает учащимся выполнить разноуровневую
самостоятельную работу. Для этого ученики (предварительно разделенные на группы) получают карточки с заданиями.
1 уровень.
Постройте график обратной пропорциональности y = с помощью таблицы.
| x | -12 | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 12 |
| y | -1 | -2 | -3 | -4 | -6 | -12 | 12 | 6 | 4 | 3 | 12 |
2 уровень.
Постройте график обратной пропорциональности y = , предварительно заполнив таблицу.
| x | -16 | -12 | -8 | -4 | -2 | -1 | 1 | 2 | 4 | 8 | 12 | 16 |
| y |
|
|
|
|
|
|
|
|
|
|
|
|
3 уровень.
Составить таблицу некоторых значений функции y = и построить ее график.
По истечении отведенного времени, правильное решение проецируется на экран.
В это время учащиеся обмениваются тетрадями и сверяют решения. Учитель очень быстро проводит опрос: «Поднимите руку, у кого нет ошибок?» По числу поднятых рук можно судить о степени усвоения материала урока.
4. Постановка домашнего задания:
Подготовить историческую справку о кривой (гипербола);
п. 8 № 179, 180 (б, в).
Подведение итогов урока.
Фронтальным опросом вместе с учащимися подводятся итоги урока:
Какая функция называется обратной пропорциональностью?
Как называется ее график?
В каких координатных четвертях расположен график функции 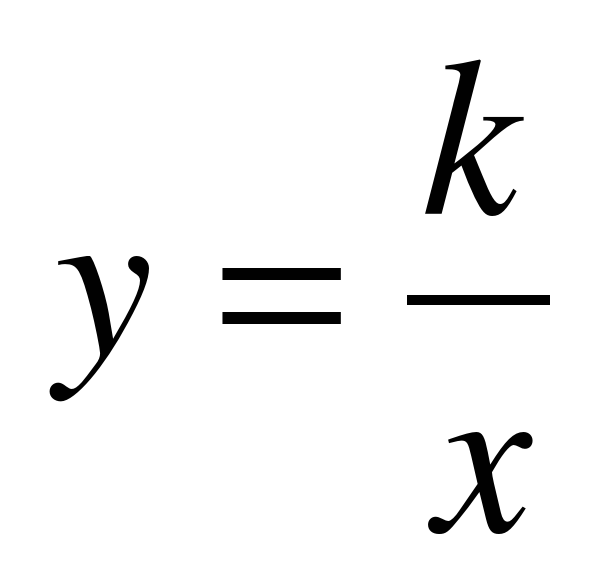 в зависимости от k?
в зависимости от k?
С учетом работы в течение всего урока комментируются и оцениваются ответы учащихся.
Приложение 1.
|
|
|
|
|
|
|
|
|
|
|
|
| 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
| |
| |
|
|
|
|
|
|
|
| 3 | | | | | 9 |
| |
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
| 5 | | | | | | |
|
|
|
|
| 10 |
|
|
| |
| |
| |
| |
|
|
|
|
|
|
|
|
| |
|
|
| |
| |
| |
|
|
|
|
|
|
|
|
|
| 8 | | | 6 | | | | | | | | 4 | | | | | | |
|
|
| |
| |
| |
| |
| |
| |
|
|
|
|
|
|
|
|
| |
| |
| |
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
| |
| |
|
| 1 1 1 7 | | | | |
|
|
|
|
|
|
|
| |
| |
| |
|
| |
|
| |
|
|
|
|
|
|
|
|
| |
| |
| |
|
| |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
|
Вопросы кроссворда.
Зависимость между переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной (Функция).
Независимая переменная (Аргумент).
Множество точек координатной плоскости, абсциссы которых равны значению аргумента, а ординаты - значениям функции (График).
Функция, заданная формулой y = kx + b (Линейная).
Каким коэффициентом называют число k в формуле y = kx + b (Угловым).
Что является графиком линейной функции? (Прямая).
Какой буквой обозначается ось абсцисс? (Икс).
Слово в названии функции y = kx (Пропорциональная).
Функция y = x2 (Квадратичная).
Название графика квадратичной функции (Парабола).
Какой буквой обозначается ось ординат (Игрек).
Один из способов задания функции (Формула).
8







 y
y
 y
y y
y 0 1 x
0 1 x
 0 1 x
0 1 x
 0 y
0 y 1 y
1 y 0 1 x
0 1 x 2 y
2 y 0 1 x
0 1 x
















