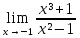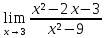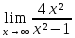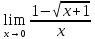Практическая работа по теме "Техника вычисления пределов" предназначена для студентов первого курса специальности 20.02.01 политехнического техникума.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Техника вычисления пределов
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Техника вычисления пределов»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2100 руб.
3000 руб.
2000 руб.
2860 руб.
2220 руб.
3170 руб.
1970 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
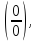 путем разложения на множители; научиться раскрывать неопределенность вида
путем разложения на множители; научиться раскрывать неопределенность вида 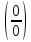 , вызванную присутствием корня; научиться вычислять пределы при
, вызванную присутствием корня; научиться вычислять пределы при 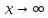 , в том числе путем раскрытия неопределенностей вида
, в том числе путем раскрытия неопределенностей вида 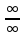 и
и 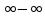 .
. 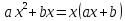
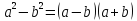
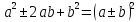
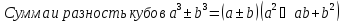
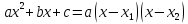 , где
, где 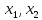 корни квадратного уравнения
корни квадратного уравнения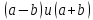 , причем их произведение дает формулу разность квадратов
, причем их произведение дает формулу разность квадратов 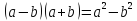
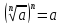
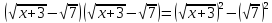 =
=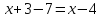
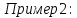
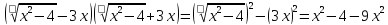
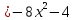
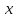 - величина бесконечно малая, то обратная ей величина
- величина бесконечно малая, то обратная ей величина 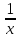 является бесконечно большой.
является бесконечно большой.
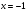 в функцию, стоящую под знаком предела. Получим,
в функцию, стоящую под знаком предела. Получим,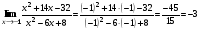 .
.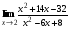 .
.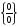 в этом случае, нужно разложить числитель и знаменатель на множители и сократить дробь на общий множитель.
в этом случае, нужно разложить числитель и знаменатель на множители и сократить дробь на общий множитель.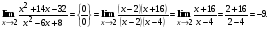
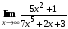 .
.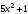 и
и 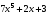 являются бесконечно большими. Поэтому,
являются бесконечно большими. Поэтому, 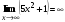 ,
,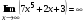 .
. .
. в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь.
в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь.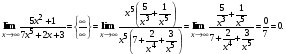
 .
.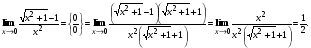
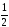 .
.