Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №1 г.Суздаля»
План-конспект урока геометрии в 8 классе по теме
«Средняя линия треугольника».
Плотникова Татьяна Владимировна – учитель математики в «МБОУ СОШ №1 г.Суздаля»
Первый урок в теме «Применение подобия к доказательству теорем и решению задач».
Учебник Л.С.Атанасян «Геометрия 7-9»
Цель урока: ознакомление учащихся с понятием средней линии треугольника; формирование умения применять свойство средней линии треугольника к решению задач..
Учебные задачи, направленные на достижение:
Личностного развития:
продолжать развивать умение ясно, точно и грамотно излагать свои мысли в устной и письменной речи,
развивать креативность мышления, инициативу, находчивость, активность при решении математических задач.
Метапредметного развития:
расширять кругозор, прививать умение совместно работать (чувство товарищества и ответственности за результаты своего труда);
продолжать развивать умение понимать и использовать математические средства наглядности.
Предметного развития:
Тип урока: урок получения новых знаний, умений и навыков.
Формы работы учащихся:
индивидуальная;
фронтальная;
работа в парах.
Необходимое оборудование:
Структура и ход урока:
Организационный момент. (Слайд №1). Сообщение темы урока. Настрой учащихся на работу.
Устные упражнения:
Решите задачи:
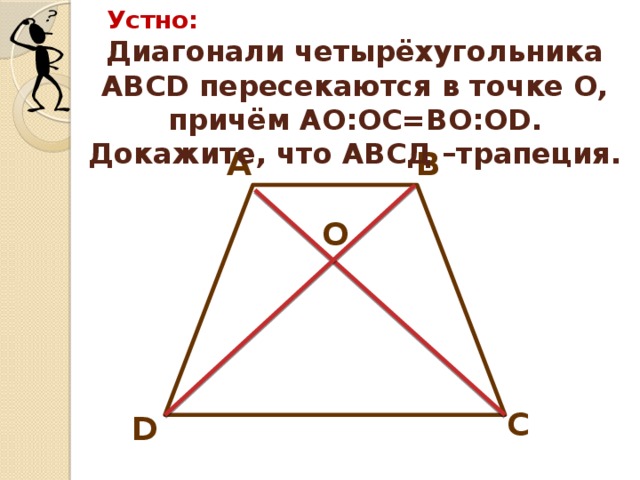
(слайд №2): Диагонали четырёхугольника АВСД пересекаются в точке О, причём АО:ОС = ВО:ОД. Докажите, что АВСД – трапеция.
(Док-во: Рассмотрим треугольники АОВ и ДОС. В них: АО:ОС = ВО:ОД – по условию задачи, угол АОВ равен углу ДОС – как вертикальные. Значит, треугольник АОВ подобен треугольнику ДОС по двум пропорциональным сторонам и углу между ними. В подобных треугольникам соответственные углы равны, значит, угол АВО равен углу ВДС, а они накрест лежащие при прямых АВ и ДС и секущей ВД. Значит, отрезок АВ параллелен отрезку ДС.
Четырёхугольник, в котором две стороны параллельны, а две другие – нет, является трапецией. АВСД – трапеция).
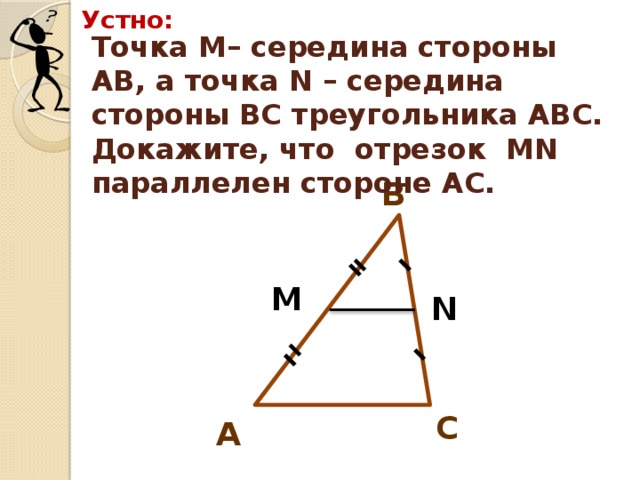
(Слайд №3): Точка М – середина стороны АВ, а точка N – середина стороны ВС треугольника АВС. Докажите, что отрезок М N параллелен стороне АС.
(Док-во: Рассмотрим треугольники АВС и ВМN. В них: угол В – общий, ВМ:АВ = ВN:ВС = 1:2. Значит, треугольник АВС подобен треугольнику ВМN по двум пропорциональным сторонам и углу между ними. В подобных треугольникам соответственные углы равны, т.е. угол ВMN равен углу ВАС, а они соответственные при прямых МN и АС и секущей АВ, значит, отрезок МN параллелен отрезку АС.)
Изучение нового материала:
(слайд №4).
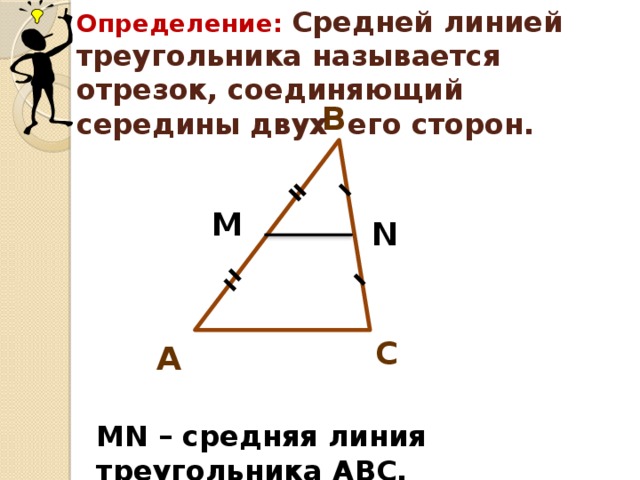
Учитель формулирует определение средней линии треугольника. Учащиеся выполняют соответствующие записи в тетради.
Вопрос к классу: Ребята, как вы думаете, а каким свойством обладает средняя линия треугольника?
Возможные ответы учащихся:
-разбивает треугольник АВС на два подобных треугольника;
-средняя линия параллельна противоположной стороне.
2. Учитель предлагает учащимся в парах обсудить доказательство параллельности
средней линии треугольника противоположной стороне. В это время учитель оказывает консультативную помощь.
Учитель: Ребята, а как вы думаете, чему равна длина средней линии треугольника? Возможно, кто-нибудь из ребят догадается, что средняя линия треугольника равна половине противоположной стороны.
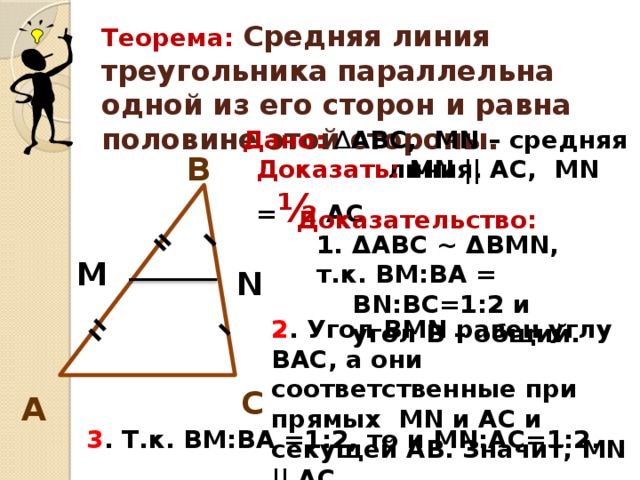
Учитель формулирует определение теорему о средней линии треугольника. (слайд №5) Учащиеся отвечают на вопросы: что дано в теореме? и что надо доказать? Делают чертёж и выполняют соответствующие записи.
Учитель предлагает учащимся в парах доказать, что средняя линия треугольника равна половине противоположной стороны, оказывая в это время консультативную помощь.
(Док-во: Рассмотрим треугольники АВС и ВМN. В них: угол В – общий, ВМ:АВ = ВN:ВС = 1:2. Значит, треугольник АВС подобен треугольнику ВМN по двум пропорциональным сторонам и углу между ними. В подобных треугольникам соответственные углы равны, т.е. угол ВMN равен углу ВАС, а они соответственные при прямых МN и АС и секущей АВ, значит, отрезок МN параллелен отрезку АС.
АС: МN = МВ:АВ=1:2,т.е.МN = ½АС)
Устное решение задач на закрепление понятия «средняя линия треугольника»:
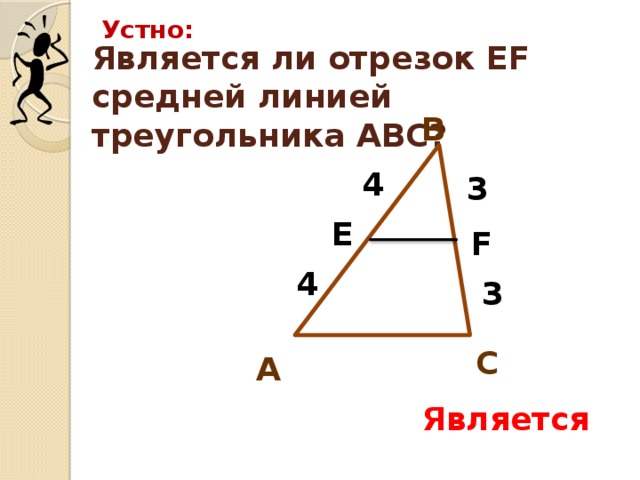
а) (слайд 6) В треугольнике АВС на сторонах АВ и ВС взяты соответственно точки Е и F так, что АЕ=ЕВ=3 см, ВF=FС-4 см. Будет ли отрезок ЕF – средней линией треугольника АВС?(да)
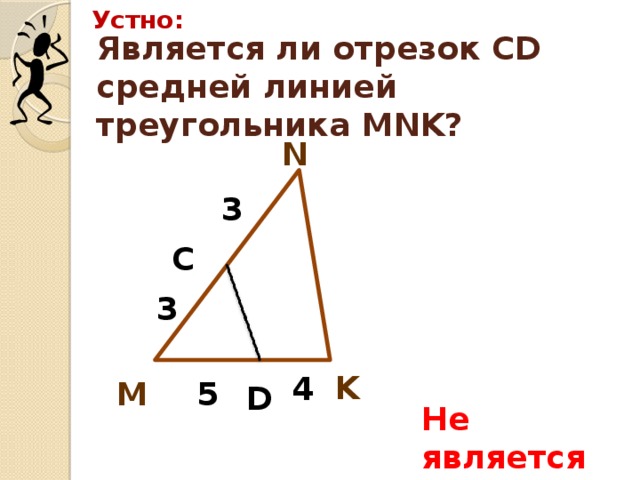
б) (слайд 7) В треугольнике MNK на сторонах MN и MK взяты соответственно точки С и Д так, что MC=CN=3см, MД=5 см, ДK=4 см. Является ли отрезок СД средней линией треугольника MNK?(нет)
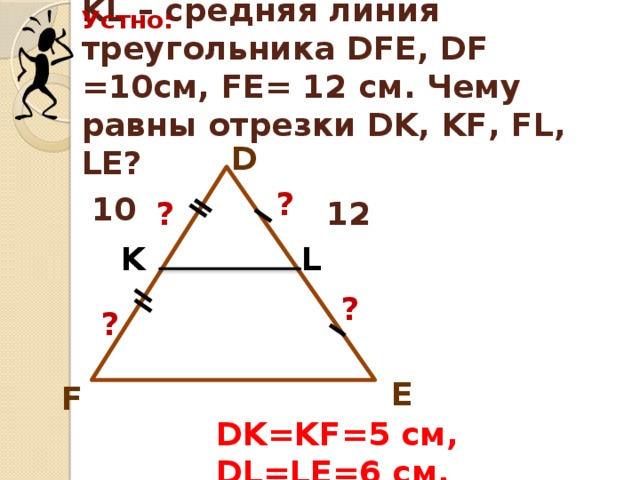
в) (слайд 8 KL – средняя линия треугольника DFE. DF=10 см, FE=12см. Чему равны длины отрезков DK,KF,FL,LE? (ДК=5см, КF=5 см, FL=LE=6 см).
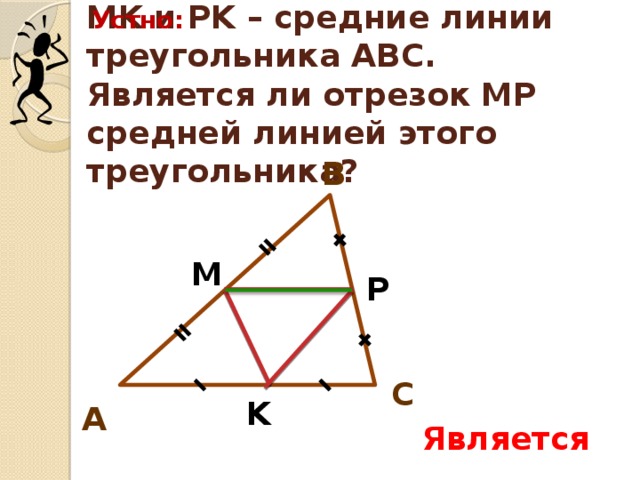
г) (слайд 9) МК и РК – средняя линия треугольника АВС. Является ли отрезок МР – средней линией этого треугольник?(да. т.к. АМ=МВ и ВР=РС)
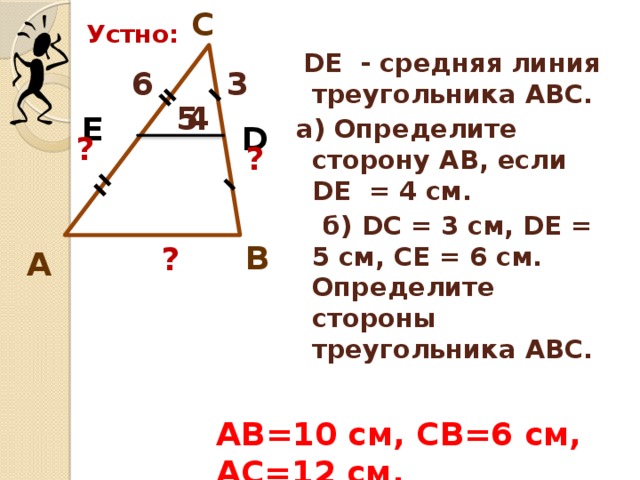
д) (слайд 10) ДЕ – средняя линия треугольника АВС. а) Определите дину стороны АВ, если ДЕ = 4 см. б)ДС=3см, ДЕ = 5 см, СЕ = 6 см. Определите длины сторон треугольника АВС.(АВ=10см, СВ=6 см, АС=12 см)
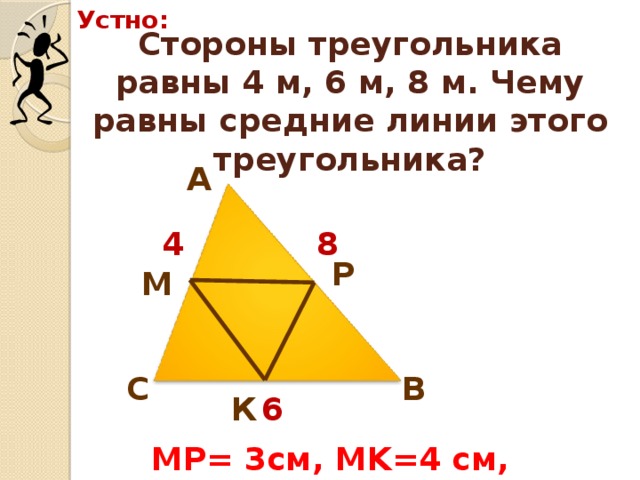
е) (слайд 11) Стороны треугольника равны 4 м, 6м, 8 м. Чему равны длины средних линий этого треугольника? (МР=3см, МК=4 см, КР=2 см)
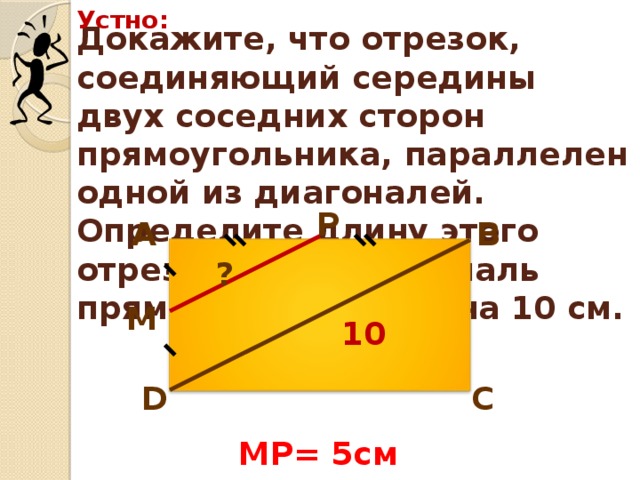
ж) (слайд 12) Докажите, что отрезок, соединяющий середины двух соседних сторон прямоугольника, параллелен одной из диагоналей. Определите длину этого отрезка, если диагональ прямоугольника равна 10 см.(МА=МД и АР=РВ, значит, МР – средняя линия треугольника АДВ. Поэтому, МР=5 см и МР||ДВ)
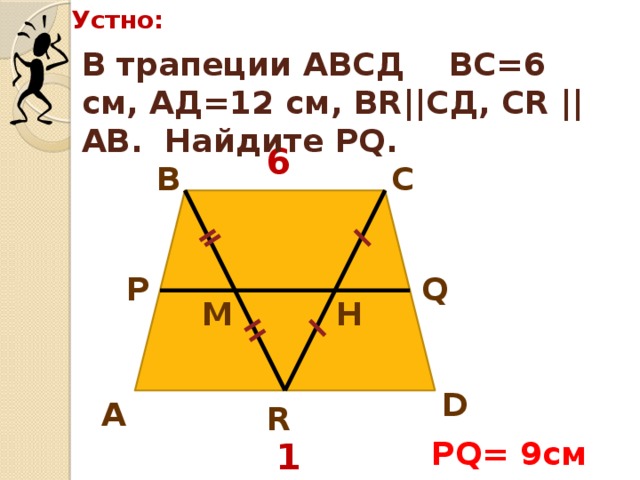
з) (слайд 13) В трапеции АВСД ВС=6 см, АД = 12 см, ВR||CД, СR||АВ. Найдите РQ.(9 см)
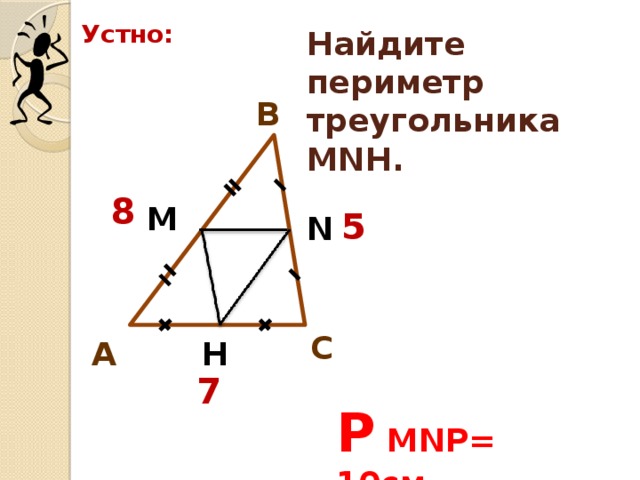
и) (слайд 14) Найдите периметр треугольника MNH, если АВ=8 см, ВС-5 см, АС=7 см, а МN,NH,MH – средние линии этого треугольника.(10 см)
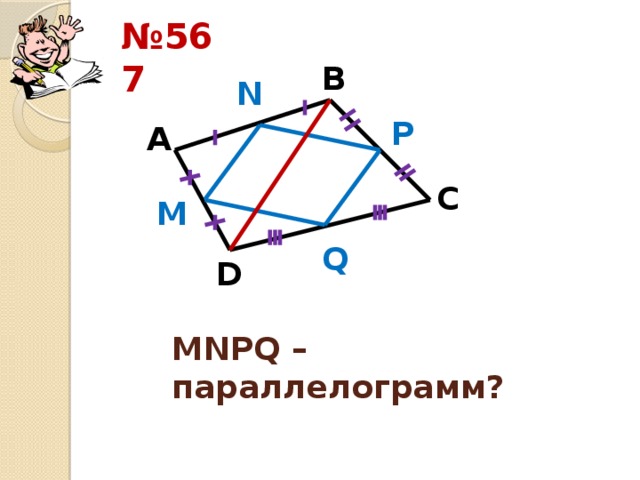
(слайд №15). Письменное решение задачи №567 из учебника.
(Треугольник АВД, АМ=МД и АN=NВ, значит, NM – средняя линия треугольника АВД. NM = ½ВД и NM||ВД.
Треугольник ВДС, BP=РС и СQ = QД, значит, PQ – средняя линия треугольника ВДС. PQ=½ВД, PQ||ВД.
NM = ½ВД и NM||ВД, а PQ=½ВД, PQ||ВД, тогда МN=PQ и МN||PQ. Четырёхугольник, в котором две стороны равны и параллельны, является параллелограммом. Значит, MNQP – параллелограмм)
Запись домашнего задания (слайд №16) п.62, №565, 566