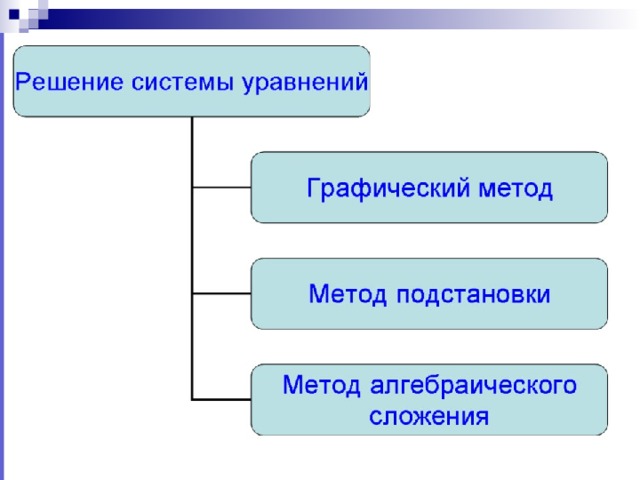
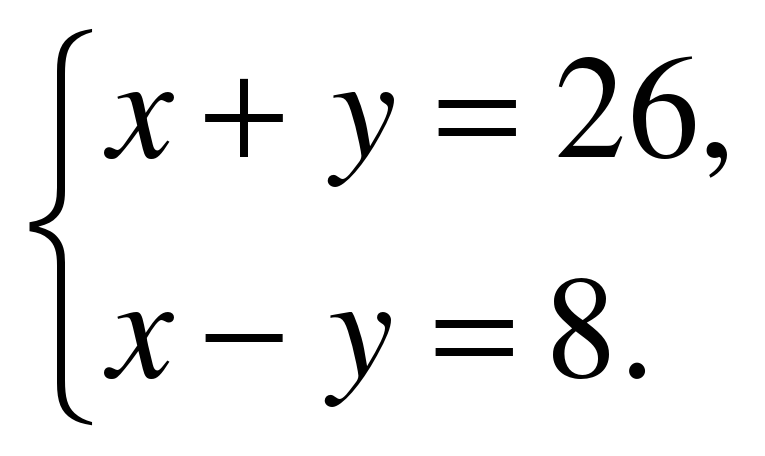Умение решать системы уравнений- хорошо, но очень скучно. А когда предлагается применить умение к решеню практических задач-увлекательно. Итак некоторые задачи решаются гораздо проще, если составить и решить систему уравнений.От учащихся потребуется проанализировать ситуацию, самостоятельно разобрать математическую модель и способ решения, грамотно выполнить проверку и записать ответ. На уроке дается алгоритм решения задач с помощью систем уравнений: построение математической модели реальной ситуации, составление системы уравнений с двумя переменными и решиние ее. В течение урока повторяются вопросы, касающиеся систем уравнений, а так же разные методы решения систем уравнений. Большое внимание уделяется графическому методу. В процессе анализа условия учащиеся выбирают наиболее удобный и простой способ решения. Наиболее сильные учащиеся решают задачи с параметром.На уроке применяются различные методы контроля и самоконтроля: устный опрос, самостоятельная и фронтальная работа. С помощью осуществления различных форм работы можно повысить активность и интерес учащихся, любознательность. Для достижения поставленных целей на уроке используются индивидуальная, парная и групповая работа. Неординарное домашнее задание: составить задачу по данной системе уравнений. На уроке используются технические средства обучения, которые позволяют моментально проверить домашнее задание, осуществить обратную связь на уроке. Работа с интерактивной доской экономит время на уроке, осуществляет коррекцию знаний, привлекает дополнительное внимание школьников. На уроке формируются навыки самостоятельной работы с информацией, умение анализировать. Ребята обучаются в условиях межличностного общения с учащимися и учителем, усваивают и отрабатывают материал в режиме диалога.
Создайте Ваш сайт учителя Курсы ПК и ППК Видеоуроки Олимпиады Вебинары для учителей
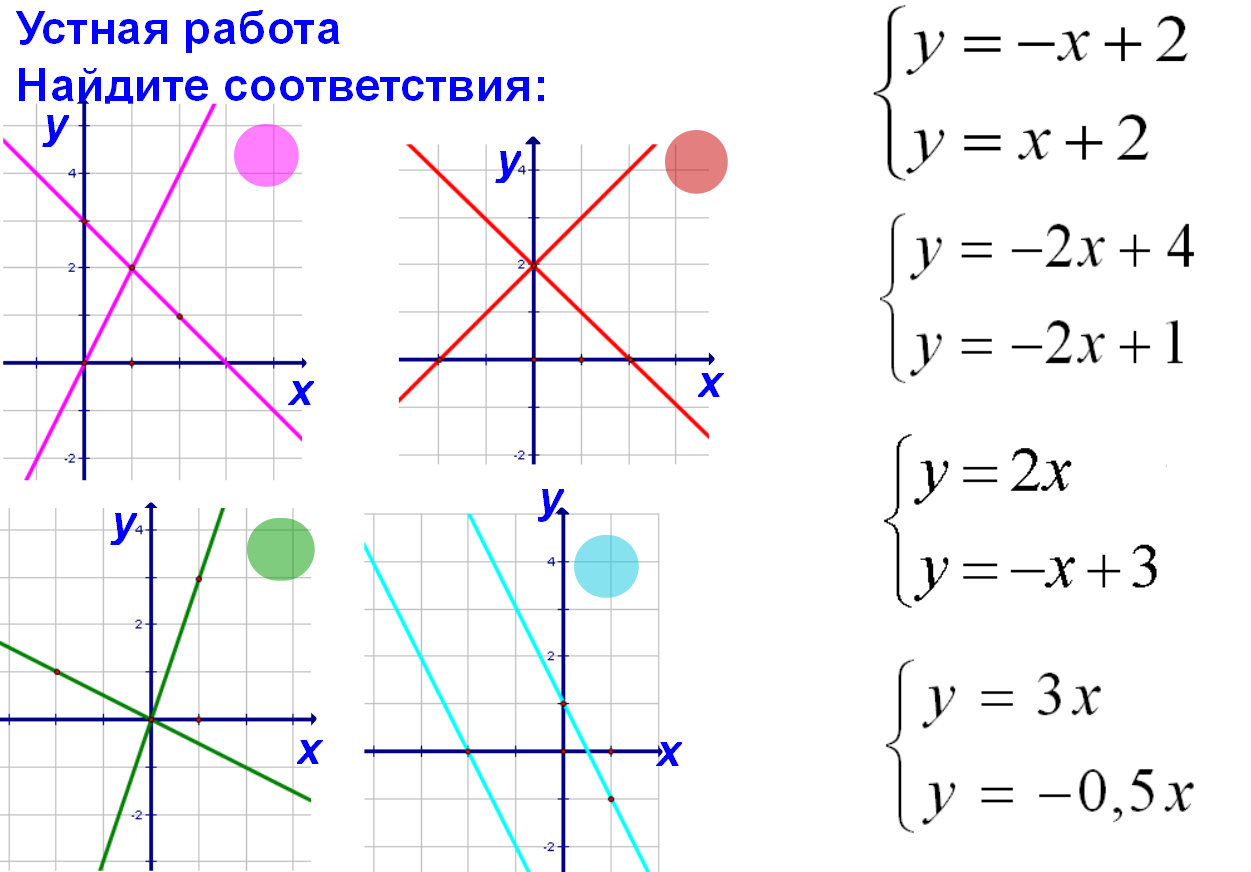
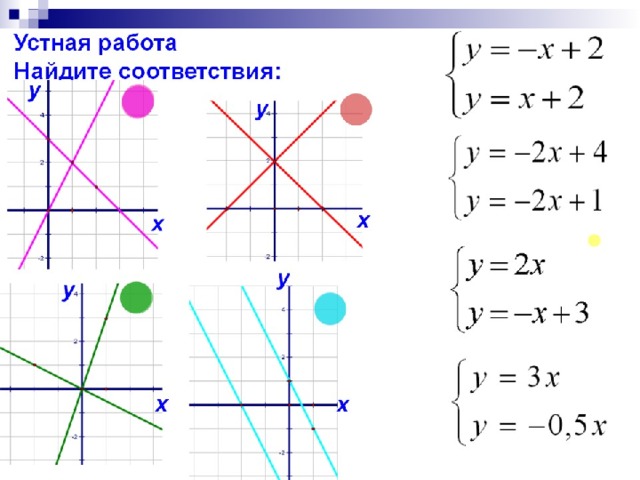
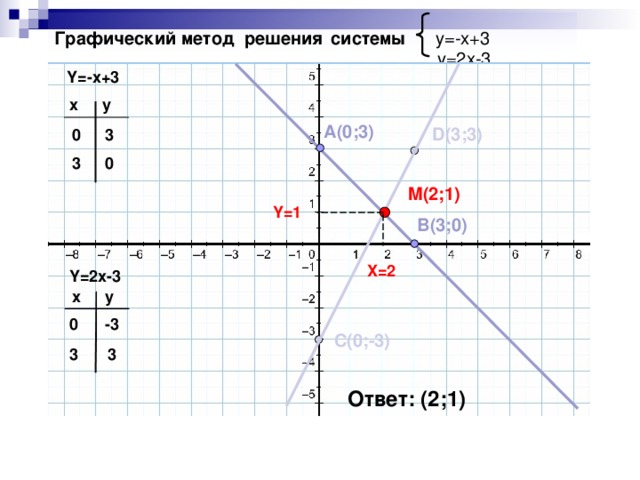
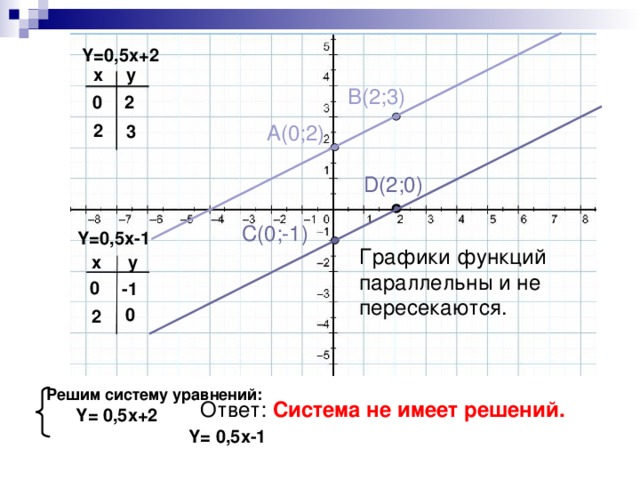
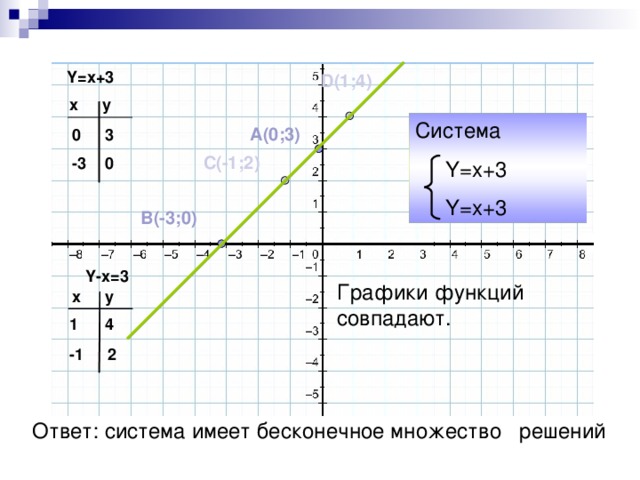
Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций
Просмотр содержимого документа
«План-конспект урока»
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 65»
План- конспект урока алгебры в 7 классе по теме:
«Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций»
Учитель математики
Мигина Любовь Викторовна
Пенза, 2014
Цели урока:
- обучающие: - развитие навыков решения систем уравнений;
- знакомство с алгоритмом решения задач при помощи системы
уравнений.
- развивающие: - развитие мышления через обучение анализировать,
сравнивать, строить аналогии;
- развитие культуры устной и письменной речи;
- развивать способность четко формулировать свои мысли;
- развитие и закрепление навыков устного счета.
- воспитательные: -
- Формирования компетентности в сфере изучения данной темы
навыка самостоятельной обработки информации; формирования
математической грамотности,
- интереса к предмету; воспитание ответственности за начатое дело;
чувство коллективизма.
Ход урока
Орг. момент, сообщение темы, постановка цели урока. (Слайд 1)
Проверка домашнего задания с помощью отсканированных на перемене решений учащихся (Приложение 3).
Актуализация знаний . Повторим теорию.
Выступление ребят с темой: «Методы решения уравнений». («Метод подстановки», «Метод сложения», «Графический метод»)
Устно.
.
5. Устная работа :
Домашнее задание
1. Решите задачу с помощью системы уравнений.
а) Сумма двух чисел равна 84, а их разность равна 20. Найдите эти числа.
Б) Скорость лодки по течении реки 18км/ч, а против течения реки 15 км/ч. Найдите собственную скорость лодки и скорость течения реки.
2. Составить системы уравнений к задачам
а) Длина ограды вокруг участка прямоугольной формы равна 140м. Одна из сторон участка на 50 м больше другой. Найдите размеры участка.
Б) Группа туристов отправилась в поход на 12 байдарках. Часть байдарок были двухместными, часть – трехместными. Сколько двухместных и сколько трехместных байдарок участвовало в походе, если группа состояла из 29 человек и все места были заняты?
3. Придумайте ситуацию, которая описывается следующей системой уравнений
8. Подведение итогов урока.
7
Просмотр содержимого презентации
«Презентация»
«Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций»
Провела: учитель математики МБОУ СОШ № 65 Мигина Л.В.
Цели:
- Вспомнить различные способы решения уравнений;
- Ответить на вопрос: зачем нужны системы уравнений ?
Проверка домашнего задания:
Мозговой штурм:
2х+у=3
Мозговой штурм:
Мини – тест
Ключ к тесту
Подберите такое значение k , при котором система
Имеет единственное
решение
У= 3х – 5
У= k х + 4
Не имеет решений
У =5х – 7
У = k х - 7
-5, -4, -3, -2, 0, 1, 2, 3, 4, 5, 6, 7
Подберите такое значение k , при котором система
Имеет единственное
решение
У= 3х – 5
У= 2 х + 4
Не имеет решений
У =5х – 7
У = 5 х - 4
-5, -4, -3, -2, 0, 1, 2 , 3, 4, 5 , 6, 7
Графический метод решения системы y=-x+3 y=2x-3
Y=-x+3
x
y
A(0;3)
D(3;3)
3
0
0
3
M(2;1)
Y=1
B(3;0)
X=2
Y=2x-3
y
x
0
-3
C(0;-3)
3
3
Ответ: (2;1)
Y=0,5x+2
x
y
B(2;3)
0
2
2
A(0;2)
3
D(2;0)
C(0;-1)
Y=0,5x-1
Графики функций параллельны и не пересекаются.
y
x
0
-1
0
2
Решим систему уравнений : Y= 0 ,5 x+2 Y= 0,5x-1
Ответ: Система не имеет решений.
Y=x+3
D( 1 ; 4 )
y
x
Система
Y=x+3
Y=x+3
A(0;3)
0
3
C( -1 ; 2 )
0
- 3
B( - 3;0)
Y -х =3
Графики функций совпадают.
y
x
4
1
2
-1
Ответ: система имеет бесконечное множество решений
Старинная задача:
- «В клетке находятся фазаны и кролики. У всех животных 35 голов и 94 ноги. Сколько в клетке кроликов и сколько фазанов?»
Арифметическое решение:
1) ( 94- 35∙2 ) : 2 = 12 - кроликов;
2) 35- 12 = 23 - фазанов.
Ответ: 12 кроликов и 23 фазана.
Решение с помощью системы уравнений:
- Ответ: 12кроликов и 23 фазана.
Основополагающий вопрос?
Зачем нужны системы уравнений?
Схема решения задач:
- Анализ условия
- Выделения двух ситуаций
- Введение неизвестных
- Составление уравнений
- Решение системы уравнений
- Запись ответа
С помощью какой из систем, можно решить следующую задачу
Сумма двух чисел равна 7, а их разность 3.Найти эти числа.
1) х-у=7
х+у=3
2) х+у=7
ху=3
3) х+у=7
Х-у=3
Опишите с помощью системы уравнений ситуацию:
- Разность двух чисел равна 12. Одно из них больше другого в 4 раза.
- В классе 36 учеников. Девочек на 3 меньше, чем мальчиков.
х – у = 12
х = 4у
х + у = 36
х – у = 3
Задачи:
- В гостинице 25 номеров. Есть 4-х местные и 2-х местные номера. Сколько каких номеров, если известно, что всего в гостинице могут разместиться 70 человек?
- Основание равнобедренного треугольника на 5 см больше его боковой стороны. Найдите стороны треугольника, если известно, что его периметр равен 50 см.
- Туристы отправились в путешествие. Сначала они решили плыть по реке и сели на пароход, который проплыл 240 км. На это он потратил 2 часа, плывя против течения , и 3 часа – по течению. Туристы решили определить, какова скорость парохода по течению и против, если известно, что за 2 часа по течению он проходит на 35 км меньше, чем за 3 часа против течения.
- Даны два числа. Если к первому прибавить половину второго, то получится 65, а если из второго вычесть третью часть первого, то получится первое число. Найдите эти числа.
Системы уравнений
1. 3.
2. 4.
Домашнее задание
1. Решите задачу с помощью системы уравнений.
а) Сумма двух чисел равна 84, а их разность равна 20. Найдите эти числа.
2. Составить системы уравнений к задачам
а) Длина ограды вокруг участка прямоугольной формы равна 140м. Одна из сторон участка на 50 м больше другой. Найдите размеры участка.
3. Придумайте ситуацию, которая описывается следующей системой уравнений
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт