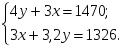Решение задач на проценты

ПрактическАЯ РАБОТА№ 7

Тема: Решение задач на проценты

Цели:

• изучить алгоритм решения задач на проценты

Оснащение занятия:   конспект лекций.

Порядок выполнения работы

Задание 1.

- Ознакомиться с лекцией № 6

- Выписать в тетрадь алгоритмы решения задач на проценты

- Записать в тетрадь решение  рассмотренных задач

Задание 2.

Решить задачи для самостоятельного решения

Лекция 5.

Тема «Решение задач на проценты»

Решение задач этого типа тесно связано с тремя алгоритмами: нахождения части от целого, восстановление целого по его известной части, нахождение процентного прироста. Рассмотрим эти алгоритмы.

1. Пусть известна некоторая величинаА, надо найтиа % этой величины.

Если считать, чтоА есть 100%, а неизвестная часть х это а %, то из пропорции

  имеем  .

1. Пусть известно, что некоторое число bсоставляета % от неизвестной величины А. Требуется найти А.

Рассуждая аналогично, из пропорции получаем .

1. Пусть некоторая переменная величинаА, зависящая от времени t, в начальный момент t0 имеет значение А0, а в момент t1 – значение А1.

Тогда абсолютный прирост величиныА за время t1–t0 будет равен А1–А0; относительный прирост этой величины вычисляется по формуле , а процентный прирост по формуле  .

Задача 1. Для офиса решили купить 4 телефона и 3 факса на сумму 1470 долларов. Удалось снизить цену на телефон на 20%, и в результате за эту же покупку уплатили 1326 долларов. Найти цену факса.

Решение:

Пусть     х – стоимость факса,

         у – стоимость телефона.

По условию    4у+3х=1470.

Так как цену на телефон снизили на 20%, то телефон стал стоить 80% от первоначальной цены, то есть

    0,8у – стоимость телефона после снижения.

По условию    3х+4×0,8у=1326.

Решим полученную систему двух уравнений методом алгебраического сложения.

Так как нам нужно найти только х, исключим у из системы, для чего первое уравнение умножим на (–0,8) и сложим со вторым:     0,6х=150  Þх=250.

Ответ: факс стоит 250 долларов.

Задачи для самостоятельного решения.

1. Из 22 кг свежих грибов получается 2,5 кг сухих грибов. Содержащих 12% воды. Какой процент воды в свежих грибах?

2. Два завода по плану должны были выпустить за месяц 360 станков. Первый завод выполнил план на 112%, а второй – на 110%, вместе заводы выпустили за месяц 400 станков. Сколько станков сверх плана выпустил каждый завод в отдельности?

3. Магазин выставил на продажутовар с наценкой 45% от закупочной цены. После продажи 0,6 всего товара магазин снизил назначенную цену на 40% и распродал оставшийся товар. Сколько процентов от закупочной цены товара составила прибыль магазина?

4. В течение третьего квартала стоимость некоторого пакета акций изменялась следующим образом: 15 августа стоимость пакета акций была на 25 % выше, чем его стоимость 1 июля, а среднее арифметическое его стоимости 30 сентября и 1 июля равнялось его стоимости 15 августа. На сколько процентов подорожал пакет акций за период с 15 августа по 30 сентября?

5. Население города за два года увеличилось с 20000 до 22050 человек. Найдите средний ежегодный процент роста населения этого города.

6. Стоимость 20 мячей до уценки составляла 900 рублей. Какое максимальное количество мячей можно приобрести на ту же сумму после их уценки на 10%?

7. Тетя Маша пошла на продуктовый рынок и купила там 1 кг черешни, после чего заметила в продаже еще черешню стоимостью 90 рублей за килограмм, что было на 10 % дешевле той, что она уже купила, и взяла еще 1 кг этих ягод. Не меньше какой суммы в рублях было у тети Маши с собой изначально?

Контроль знаний обучающихся:

• проверить практическую работу;

Требования к оформлению  практической  работы:

Задание должно быть выполнено в тетради для практических  работ

Работу сдать после занятия.