Открытый урок
по теме "Решение ключевых задач по теме теорема Пифагора"
Цели:
- формирование умений и навыков по применению теоремы Пифагора при решении простейших геометрических задач;
- формирование умений и навыков по применению формул площадей фигур при решении задач, умение соотносить формулу и соответствующую ей фигуру, умения комбинировать типовые задачи для решения более сложных задач, формирование навыков решения усложненных задач;
- создание условий для самоконтроля и взаимоконтроля усвоения знаний, воспитание культуры общения, формирование ценностных отношений;
- развитие логического мышления, формирование умений по использованию приемов сравнения, анализа, переноса знаний в новую ситуацию, формирование понимания взаимосвязи данных и искомых задачи, развитие творческих способностей учащихся.
Ход урока.
1. Орг. момент
2. Устная работа
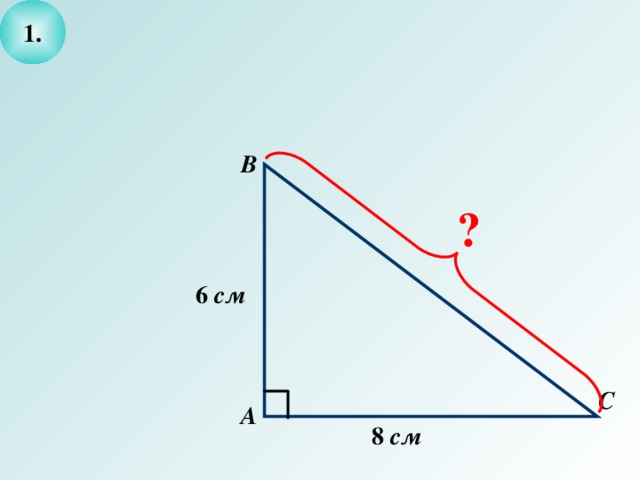
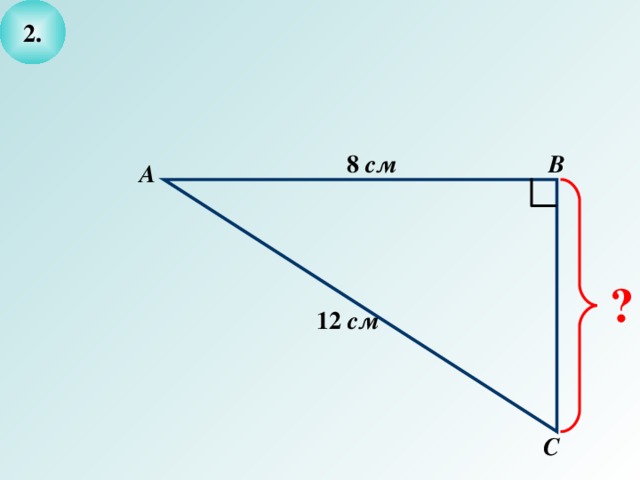
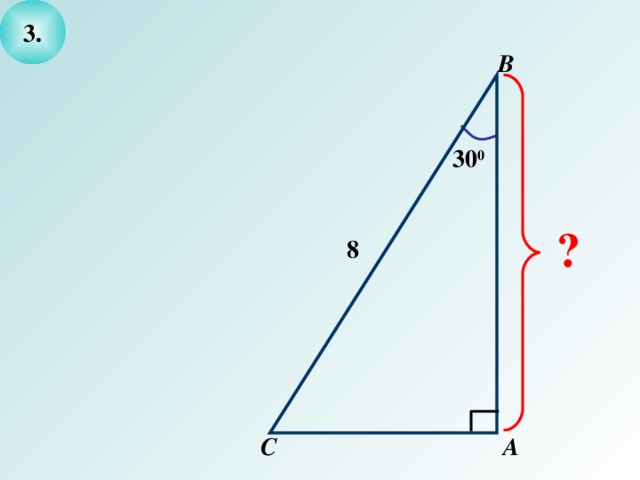
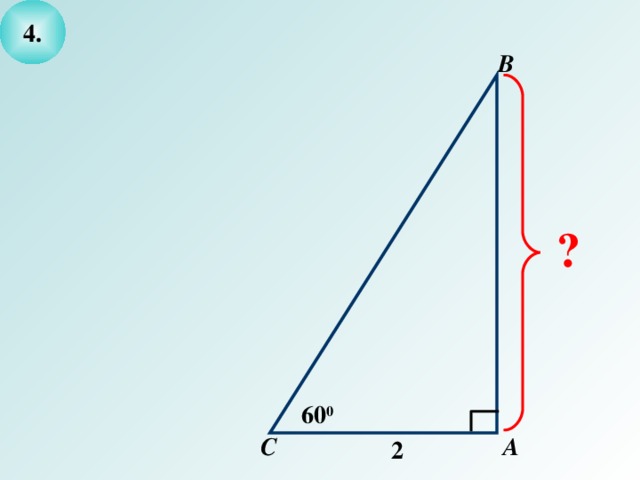
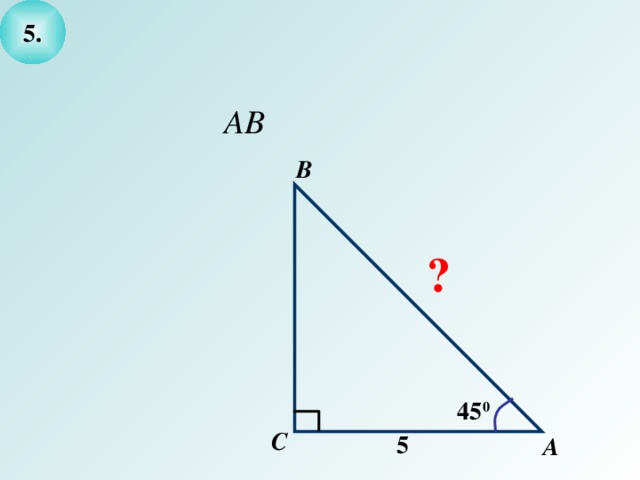
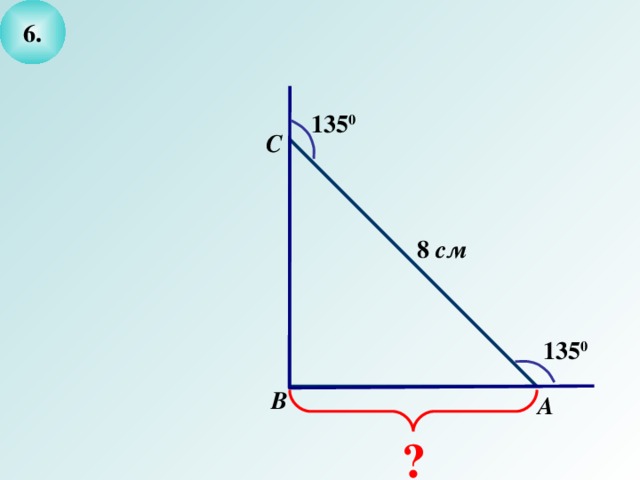
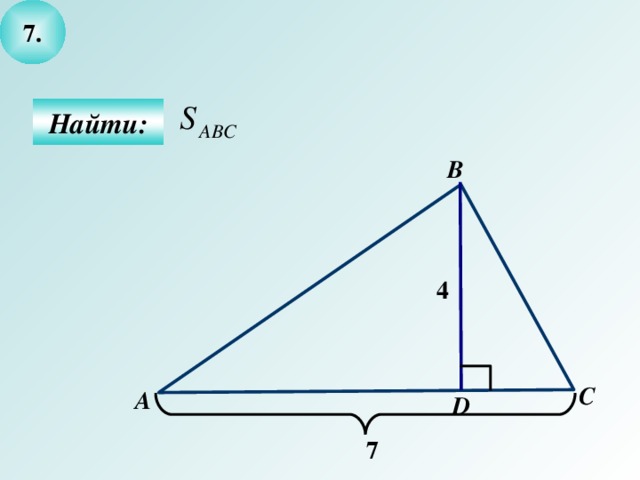
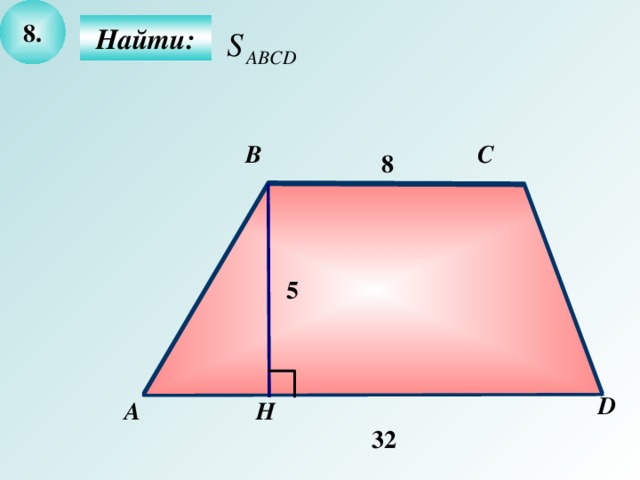
- Выделите условие и заключение задачи и решите ее.

7
4
8
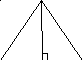
х
8
1350
1350

5
х
450
2
600
х
300
6
х
х
х
8
12
8




Найти S
8

Найти S 5
ОТВЕТЫ: 32
- Какой теоретический материал вы использовали при решении этих задач?
(Отв: свойства прямоугольных треугольников, теорему Пифагора, формулы площадей треугольника и трапеции)
- Что объединяет все эти задачи?
(Отв: использование теоремы Пифагора)
- Сегодня на уроке будем решать задачи на применение теоремы Пифагора. Итак, начнем.
3. Решение ключевых задач по теме
Задача №1 (по готовому чертежу)
(записи учитель ведет на доске, ученики - в тетради).
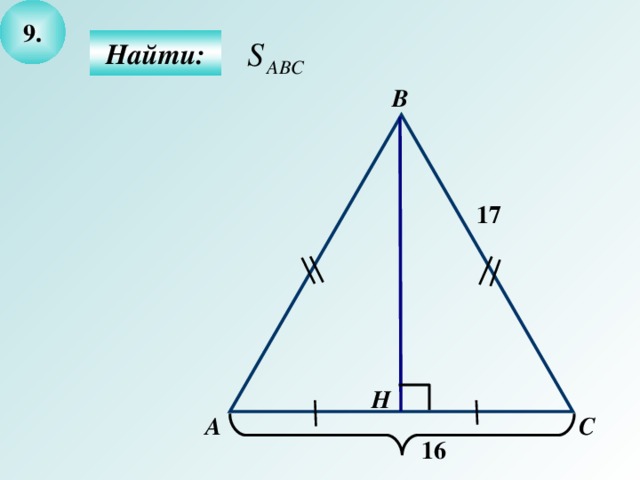
Боковая сторона равнобедренного треугольника АВС равна 17, а основание равно 16. Найдите площадь треугольника АВС
 - Что необходимо знать, чтобы найти площадь треугольника?
- Что необходимо знать, чтобы найти площадь треугольника?
- Что известно в задаче? Какого элемента не хватает?
- Какой отрезок треугольника удобно рассмотреть в качестве высоты?
- Провели ВН. Какую геометрическую фигуру надо рассмотреть для нахождения длины отрезка ВН?
- Что в треугольнике ВНС известно? Что нужно найти?
- С помощью какого теоретического материала это можно сделать?
РЕШЕНИЕ:
1. Дополнительное построение ВНАС.
2. ВН - высота ΔАВС, зн. ВН - медиана ΔАВС (по свойству высоты р/б треугольника), т.е. АН=НС=8
3. ΔВНС - прямоугольный. По теореме Пифагора 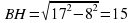
4. S ΔАВС = 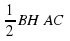 = 0,51516 = 120
= 0,51516 = 120
Ответ: S ΔАВС =120
Проанализируем задачу:
- Какая задача стояла перед нами? (найти площадь треугольника)
- Что было известно? (основание)
- Какой прием для нахождения площади использовали? (провели высоту, рассмотрели прямоугольный треугольник, воспользовались теоремой Пифагора)
- Решим следующую задачу.
Задача №2 (по готовому чертежу - письменно).
Боковая сторона равнобедренного треугольника АВС равна а, а основание равно b. Найдите площадь треугольника АВС.
- Чем эта задача отличается от предыдущей? (отв: стороны заданы буками)
- Проведите рассуждения по решению этой задачи.
РЕШЕНИЕ:
1. Дополнительное построение ВНАС.
2. ВН - высота ΔАВС, зн. ВН - медиана ΔАВС (по свойству высоты р/б треугольника), т.е. АН=НС=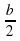
3. ΔВНС - прямоугольный. По теореме Пифагора 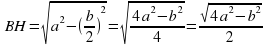
4. S ΔАВС = 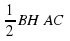 = 0,5
= 0,5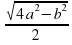 b =
b = 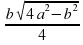
Ответ: S ΔАВС =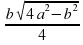
Задача №3.
- Изменим условие задачи и рассмотрим равносторонний треугольник АВС со стороной a. Найдите площадь равностороннего треугольника.
- Можно ли связать решение этой задачи с ранее решенными? Почему?
(Отв: связать можно, так как равносторонний треугольник - это частный случай равнобедренного треугольника)
- Что нужно изменить, чтобы получить площадь равностороннего треугольника? (Отв: воспользоваться формулой площади равнобедренного треугольника, заменив b на a)
РЕШЕНИЕ.
S ΔАВС =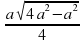 =
=
- Итак, площадь равностороннего треугольника можно вычислить по формуле S ΔАВС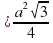
Таким образом, на этом этапе изучения темы мы получили формулу для нахождения площади равностороннего треугольника. В дальнейшем ее можно использовать как факт, как теорему. Сформулируйте ее еще раз.
- Решите устно:
Найти площадь равностороннего треугольника, если сторона равна 5 см; 1,2 см
- Какой еще тип задач можно решать, используя эту формулу?
(Отв: находить сторону равностороннего треугольника по известной площади)
Задача №4 (по готовому чертежу)
(записи учитель ведет на доске, ученики - в тетради)
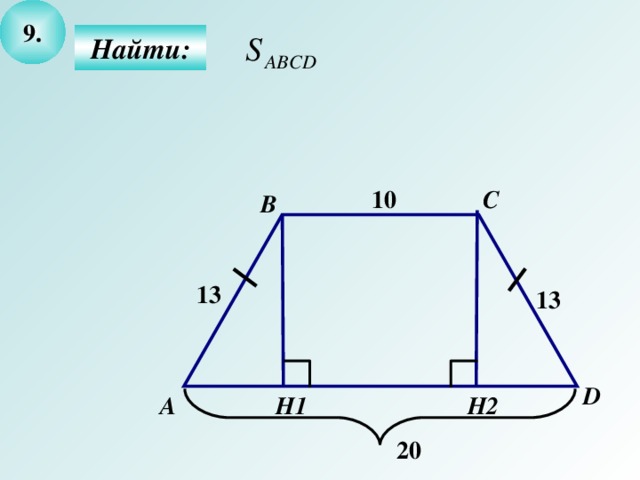
Найдите площадь трапеции ABCD, если AB и CD - основания, AB = 10, BC = AD = 13 см, CD = 20 см.
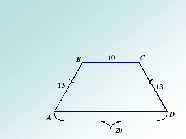 - Какая геометрическая фигура задана?
- Какая геометрическая фигура задана?
- Что известно? Что необходимо найти?
- Достаточно ли данных, чтобы ответить на вопрос задачи?
- Какое дополнительное построение нужно выполнить в этом случае? (Отв: провести высоту из вершины В)
- На что обращаем внимание? (Отв: одной высоты недостаточно, проведем еще высоту из вершины С)
- Как правило, если речь идет о трапеции, то проводить нужно две высоты.
РЕШЕНИЕ:
1. Дополнительное построение ВН1АD, CH2 AD.
2. Рассмотрим прямоугольные треугольники АВН1 и CDH2: ВН1 = СН2 (как отрезки параллельных прямых, заключенных между параллельными прямыми), АВ = CD (по условию), зн. ΔABH1= ΔDCH2 (по катету и гипотенузе), т.е. АН1 = DH2.
3. ВН1 и СН2 - высоты трапеции, зн. ВН1Н2С - прямоугольник, т.е. Н1Н2 =ВС =10(по свойству прямоугольника), тогда АН1 = DH2 = 5.
4. ΔВН1А - прямоугольный. По теореме Пифагора 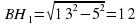
5. S АВСD = 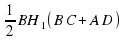 = 0,512(10+20) = 180
= 0,512(10+20) = 180
Ответ: S АВСD =180
Проанализируем задачу:
- Какая задача стояла перед нами? (найти площадь трапеции)
- Что было известно? (основания, боковые стороны)
- Какой прием для нахождения площади использовали? (провели высоты, рассмотрели прямоугольный треугольник, воспользовались теоремой Пифагора)
- Задачи с какими геометрическими фигурами рассмотрели? (Отв: треугольник трапеция)
- В каких еще геометрических фигурах можно выделить прямоугольные треугольники? (Отв: параллелограмм, ромб)
Задача №5 (устно)
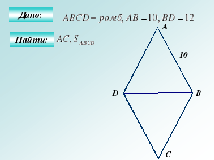 - Какая геометрическая фигура задана?
- Какая геометрическая фигура задана?
- Что известно? Что необходимо найти?
- Достаточно ли данных, чтобы ответить на вопрос задачи?
- Какое дополнительное построение нужно выполнить в этом случае? (Отв: провести диагональ АС)
- Каким свойством обладают диагонали ромба?
- Какую геометрическую фигуру надо рассмотреть для нахождения длины отрезка АС?
- Что в треугольнике АОВ известно? Что нужно найти?
- С помощью какого теоретического материала это можно сделать?
РЕШЕНИЕ:
1. Дополнительное построение АС.
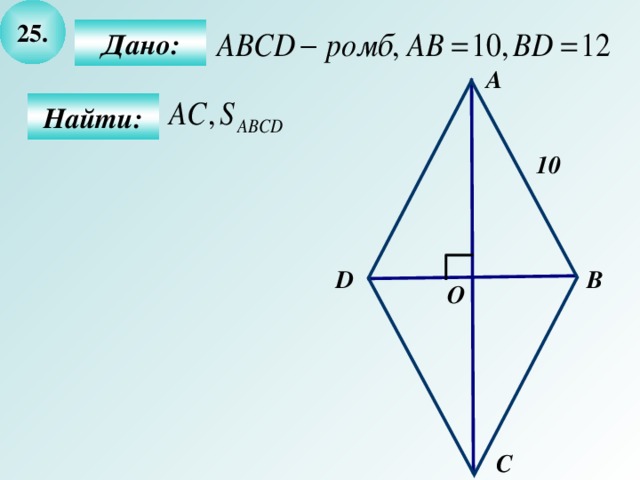
2. ABCD - ромб, AB = AD = 10 (по определению), зн. ΔАВD - равнобедренный
3. АСBD, DO = ОВ (по свойству диагоналей ромба), ΔАВО - прямоугольный, зн. по теореме Пифагора 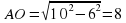 , т.е. АС = 2АО = 16.
, т.е. АС = 2АО = 16.
4. S АВСD = 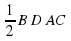 = 0,51216 = 96
= 0,51216 = 96
Ответ: S АВСD =96
4. Итоги урока
- Что объединяет рассмотренные сегодня на уроке задачи?
(Отв: 1) даны фигуры, площади которых нужно было найти,
2) везде выполняли дополнительные построения,
3) рассматривали прямоугольные треугольники, в которых один элемент был известен, а другой находили из свойств геометрических фигур
4) Использовали теорему Пифагора для нахождения неизвестного элемента)
- В каких геометрических фигурах выполняли дополнительное построение? Сколько высот достаточно провести в каждом случае?
- Какие геометрические фигуры мы не рассмотрели на уроке? Будет ли отличаться идея решение задач в этом случае?
- Какой новый факт вы узнали? Будете ли его использовать в дальнейшем?
ВЫВОД: задачи, рассмотренные нами, дают "ключ" к решению целого ряда задач на нахождение площадей многоугольников. Количество задач на нахождение площадей фигур увеличилось за счет возможности использования теоремы Пифагора.
5. Рефлексия
- Сегодня на уроке я повторил...
- Сегодня на уроке я узнал...
- Сегодня на уроке я научился...
6. Домашнее задание
п.54, 55(вопр.1-10), №493, 490(б), 489(в)







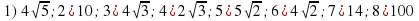
 - Что необходимо знать, чтобы найти площадь треугольника?
- Что необходимо знать, чтобы найти площадь треугольника?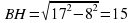
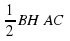
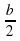
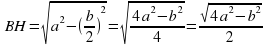
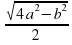
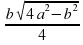
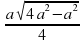 =
=
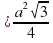
 - Какая геометрическая фигура задана?
- Какая геометрическая фигура задана?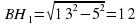
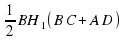 = 0,5
= 0,5 - Какая геометрическая фигура задана?
- Какая геометрическая фигура задана?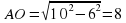 , т.е. АС = 2АО = 16.
, т.е. АС = 2АО = 16.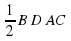 = 0,5
= 0,5