компьютер, экран, проекционный аппарат.
| № п/п | Этап урока | Задачи этапа | Деятельность учителя | Деятельность учащихся | Результаты (формируемые УУД) |
| I | Организационный момент (2 мин).
Готовность класса к работе, организация внимания всех учащихся. | Создать положительный эмоциональный настрой; совместно с учащимися сформулировать тему и цель урока значимую для учащихся. | Приветствует учащихся. Предлагает прочитать эпиграф урока. Заполнить пропущенные слова в теме урока, начало которой написано на доске. Предлагает определить тему урока и побуждает учащихся к постановке целей и задач урока.
| Приветствуют учителя и друг друга. Выполняют предложенные действия. Рассказывают, как они поняли слова, записанные в эпиграфе. Предлагают дописать тему «Решение задач…» Формулируют с помощью учителя тему, цель и задачи урока.
| Коммуникативные (слушают товарищей, делают свои предположения, выражают свои мысли). |
| II | Опрос учащихся по заданному на дом материалу (8 мин).
Возможность в ходе проверки скорректировать опорные понятия. | Повторить способы решения систем линейных уравнений. Проконтролировать навыки решения систем. Устранить в ходе проверки обнаруженные пробелы в знаниях | Отвечает на вопросы уч-ся по д/з, проводит разбор нерешенных заданий. Предлагает самостоятельно решить системы уравнений: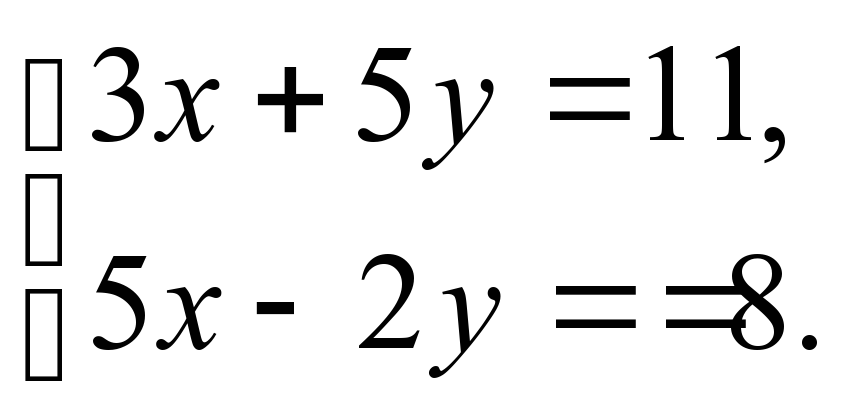 
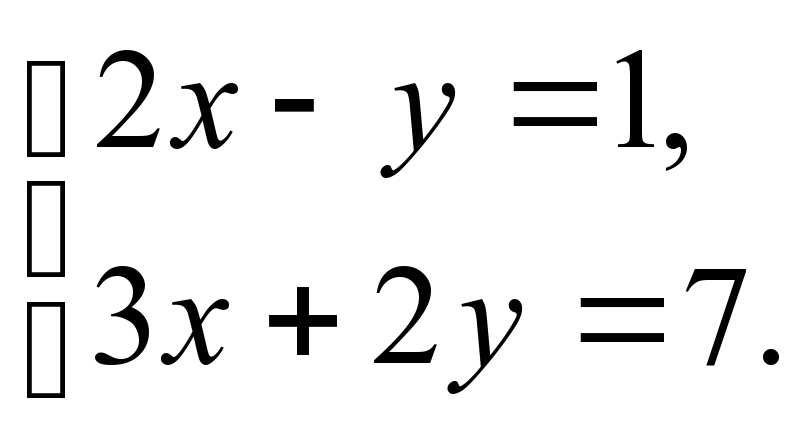
| Рассказывают: какими способами и как решали системы уравнений. Задают вопросы, возникшие при решении домашнего задания. Самостоятельно решают предложенные системы. (3-4 ученика, верно выполнивших работу, получают оценки и идут помогать другим уч-ся).
| Познавательные, коммуникативные, регулятивные. |
| III | Изучение нового учебного материала (15 мин)
Правильность ответов и действий учащихся в процессе беседы, активное участие в подведении итогов самостоятельной работы. | Составить алгоритм решения задач с помощью систем уравнений. Освоить навыки применения нового алгоритма. Подвести всех уч-ся к осознанию, обобщению и систематизации новых знаний | 1.Предлагает решить задачу № 1(задачу можно решить несколькими способами), принимает любой способ решения, но если никто из уч-ся не сможет предложить способ решения соответствующий теме урока, наводящими вопросами подводит к решению с помощью системы уравнений. 2.Предлагает оформить все найденные способы решения на доске и сравнить их. 3.Предлагает решить задачу № 2, самостоятельно определив способ решения (задача решается только с помощью системы). | В процессе решения вырабатывают алгоритм решения задачи с помощью системы уравнений: 1.Прочитать текст задачи. 2. В соответствии с условием задачи ввести переменные величины. 3.Составить систему уравнений. 4. Решить систему уравнений. 5.Проанализировать полученные решения, отобрать решения, удовлетворяющие условию задачи. 6.Записать ответ, (алгоритм решения записывают в тетрадь). При решении задачи №2 приходят к выводу, что ее можно решить только с помощью системы уравнений, значит знание нового алгоритма необходимо. Первый, верно решивший задачу ученик, оформляет решение на доске. Остальные проводят самопроверку, анализируют, исправляют ошибки, выясняют непонятое.
| Познавательные (работа с текстовой информацией). Коммуникативные (обсуждают способы решения). Регулятивные (контролируют скорость решения, соотносят текст и решение задач с соответствующей моделью) |
| IV | Первичное закрепление нового материала (10 мин)
Умения уч-ся воспроизводить основные идеи нового материала, соотносить между собой текст и математическую модель. Активность всех учащихся. | Осмыслить приобретенные знания и навыки. Уметь применять их в новой обстановке. Контроль и коррекция новых знаний. | Предлагает по тексту задачи № 3 и уже составленной системе определить, соотносятся ли они между собой и ответить на поставленный вопрос. Организует обсуждение способов решения и оценочные высказывания обучающихся. Обеспечивает положительную реакцию уч-ся на высказывания и предложения одноклассников. Предлагает решить систему и сделать вывод. | Ученики, не решая систему, анализируют текст задачи, рассуждают, делают вывод: подходит ли данная система по смыслу для решения данной задачи. Рассуждают, по тексту задачи утверждают, что система подходит, но решив ее, обнаруживают несоответствие. Делают вывод о том, что математическую модель надо обязательно подвергать критическому анализу, проверять на соответствие текст и предложенную математическую модель. | Коммуникативные (умение выражать грамотно и убедительно свои мысли). Личностные (формирование математической компетентности) |
| V | Постановка домашнего задания (3мин)
Правильное выполнение д/з всеми уч-ся. | Разъяснить уч-ся методику выполнения и самопроверки д/з (д/з должно быть дифференцированным) Составить синквейн на тему «Система» или «Задача». | Информирует о д/з. Делает пояснения по его выполнению. Проверяет понимание уч-ся содержания работы. Предлагает выбрать каждому самостоятельно задания своего уровня. | Проговаривают по цепочке критерии правильного выполнения д/з (аккуратность, правильность, рациональность решения), анализируют, делятся планами. | Умения выражать свои мысли, анализ действий, самоконтроль. |
| VI | Подведение итогов урока (2 мин)
Активное участие уч-ся в адекватной оценке собственной деятельности на уроке. | Проанализировать степень достижения цели и наметить перспективу на будущее | Аргументация выставленных оценок, замечания по уроку, оценка работы класса | 1.Участие в оценке собственной деятельности на уроке. 2. Осознание значимости полученных результатов. 3.Высказывают личное мнение об уроке.
| Развитие монологической и диалогической речи, анализ собственных действий. |
В клетке находится неизвестное число фазанов и кроликов. Известно, что в клетке находится 35 голов и 94 лапы. Узнать сколько фазанов и сколько кроликов находится в клетке?
В трех тетрадях и четырех блокнотах вместе 108 страниц. В двух блокнотах столько же страниц, сколько их в трех тетрадях. Сколько страниц в каждой тетради и в каждом блокноте?
для решения задачи «Если бы купили 4 м одной ткани и 5 м другой, то заплатили бы 800 рублей, а если бы первой купили 6 м, а второй 7 м, то заплатили бы 1000 рублей. Сколько стоит 1 м каждой ткани?» 
