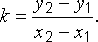Lesson study.Математика 8 класс. Решение задач с помощью системы линейных уравнений8

Предмет:

Математика

Класс:

8

Учитель:

Адилгалиева Жанлыш Салыковна

Раздел:

8.3В. Решение уравнении

Тема:

Решение задач с помощью систем уравнений

Тип урока:

Форма урока:

Урок применения знаний на практике

Цели обучения, которые будут достигнуты с помощью данного урока

АУ 8.10 знает способы решения систем уравнений (способ подстановки, способ сложения, графический способ);

МР 8.2 составляет и решает системы линейных уравнений по условиям текстовых задач

Цели урока:

Показать использование системы линейных уравнений как математической модели реальной ситуации

Применение знаний по теме "Системы линейных уравнений" для решения текстовых задач.

Учить анализировать условие задачи и выбирать более простой способ решения

Языковые цели:

Учащиеся узнают и смогут объяснить, как решаются текстовые задачи с помощью составления системы линейных уравнении.

Интеграция дисциплин:

Математика, казахский язык, английский язык

Предыдущее обучение:

Учащиеся повторили алгоритм решения систем уравнений различными способами.

Школьные ценности

Академическая честность, сотрудничество.

 Уважение по отношению к себе и окружающим

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Организационный момент

2 мин

Объединение в группы по 3-4 ученика.

Распределение обязанностей в группе. Знакомство с критериями оценивания групповой работы. (Критерии С и D по Блуму). Формулировка учащимися целей урока и темы урока. (W/ G)

Начало урока

3 минут

Эпиграф урока:

«Всякая хорошо решенная математическая задача доставляет умственное наслаждение»

Г.Гессе

Мотивация учеников

Я хочу загадать вам загадку:

Что самое быстрое, но и самое медленное.

Самое большое, но и самое маленькое.

Самое продолжительное, но и самое краткое.

Самое дорогое, но и дёшево ценимое нами?

Это ребята – время.

У нас всего 80 мин, но мне бы очень хотелось, чтобы они не тянулись, а пролетели. Не оказались прожитыми впустую, а были затрачены с пользой.

Работа в классе

5 мин

Работа в паре

5 мин

Стратегия «Ball Toss (мяч вопросов и ответов – Сұраққа жауап»
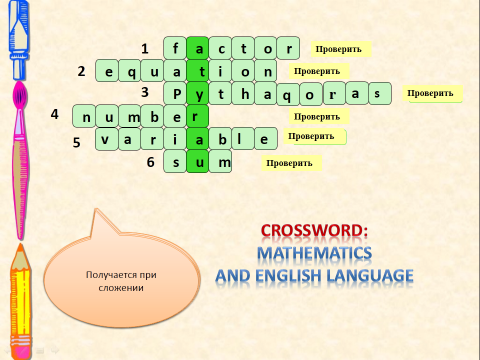
To recall the theoretical material on the subject, let's unravel the next puzzle.

W: Students one suited to the board and answer questions crossword.

Questions in Russian, but the answers must be in English.

1. Наибольший общий ….

2. Равенство, которое выполняется лишь при некоторых значениях входящих в него букв

3. Древнегреческий ученый VI века до н.э

4. Натуральное ….

5. Величина, характеризующаяся множеством значении, которая она может принимать

6. Получается при сложении

По вертикали получилось слово «ATYRAU»

Сегодня мы с вами поговорим о нашем городе - Атырау.

Атыра́у (каз. Атырау (инф.) рус. — дельта;

до 4 октября 1991 года Гурьев) — город, областной центр Атырауской области Республики Казахстан. Расположен в европейской (западной) части Казахстана, по берегам реки Урал (на момент основания — находился в месте впадения реки в Каспийское море, однако отдалился от него вследствие падения уровня Каспия). Нефтяная столица Казахстана

Историческая справка:

В 1640 году был основан город Гурьев. Ярославский купец Гурий Назарьев со своими сыновьями построил в устье реки Жайык (Яик) на правом ее берегу, деревянный острог (укрепление), поблизости от рыбачей стоянки Уйшик («учуг» - приспособление для рыбной ловли заградительного типа), уплатив дань Ногайскому ханству в Сарай-Джуке. В 1810-15 гг. крепость была упразднена. 

С 1885 года - уездный город на территории Уральского казачьего войска.

Продолжаем решать текстовые задачи с помощью системы линейных уравнений.

Повторим алгоритм решения:

• Отметить две неизвестные величины буквами.

• Составить буквенные выражения по условию задачи.

• С помощью буквенных выражений составить систему двух уравнений.

• Решить систему уравнений.

• Предоставить величинам найденных значений, проверить соответствие условии задачи.

• Записать в ответ значения величин, о которых говорилось в условии задачи.

Тапсырма: Ауызша есептеуді қайталаймыз. «Лото» ойыны.Дұрыс жауабын табыңыз:

Сыртқы беті

Келесі беті

Презентация

«Решение задач с помощью системы линейных уравнений с двумя неизвестными»

Задачник Мордкович 7 класс

Учебник Алгебра Макарычев 7 класс

Групповая работа

5 мин

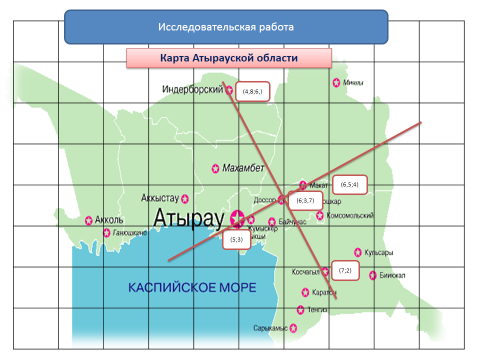
Исследовательская работа

20 мин

Стратегия «Grab bag –мешок заданий – қоржындағы тапсырмалар»

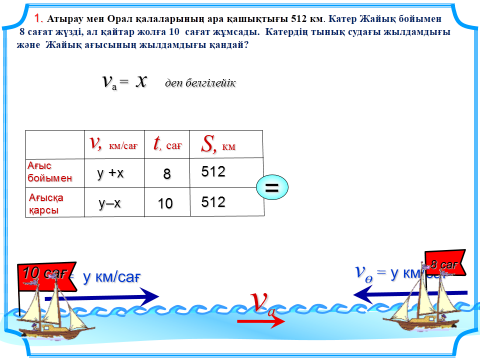
Тапсырма: Мәтіндік есептің математикалық моделін құрындар

Шешуі: егер х – ағыс жылдамдығы, у – катер жылдамдығы болса, онда:

2 у =115,2 х = 64 – 57,6

у = 57,6 х=6,4

Жауабы: 6,4 км/сағ; 57,6 км/сағ

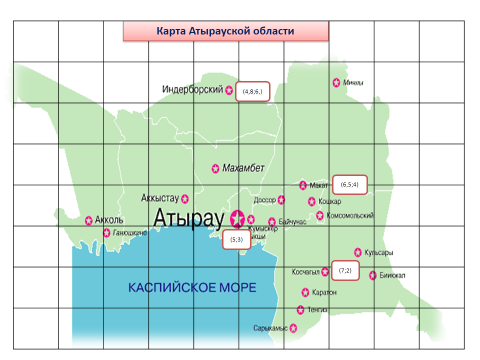
Задание № 2. График I линейной функции проходит через точки А (5;3) и В (6,5; 4), график II линейной функции проходит через точки С (4,8; 6) и

D (7;2). Имеют ли графики функции общие точки?

Решение:

Если даны две точки , то уравнение прямой, проходящей через них, определяется по формуле

.

Затем можно привести полученное уравнение к общему виду, или к уравнению с угловым коэффициентом. Умножим обе части (3) на , очевидно, что угловой коэффициент имеет вид

а) Составим уравнение І прямой, проходящей через точки А(5;3), В(6,5;4)

Полагая х₁=5, у₁ =3, х₂=6,5, у₂=4, получим

После упрощения получаем искомое уравнение в виде:

1,5 у - х+0,5 =0

у =

б) Составим уравнение ІІ прямой, проходящей через точки С(4,8;6), D(7;2)

Пологая х₁=4,8, у₁ =6, х₂=7, у₂=2, получим

После упрощения получаем искомое уравнение в виде:

2,2 у +4 х-32,4 =0

у =

в) Найдем точки пересечения двух прямых:

=

82 х = 497 у =

х = 6 у =

Две прямые пересекаются в точке (6; 3. Точка соответствует на карте Атырауской области поселку Доссор.

Доссор (каз. Доссор) — посёлок городского типа в Макатском районе Атырауской области Казахстана. Административный центр и единственный населённый пункт Доссорской поселковой администрации. Расположен в 95 км к северо-востоку от Атырау.
Один из первых центров добычи нефти в Эмбинском нефтяном районе – 1911 год.

Задачник Мордкович 7 класс

Учебник Алгебра Макарычев 7 класс

Минута психологической разгрузки

Второй урок

Решение задач

10 мин

Решение дифференцированных задании

20 мин

Закройте глаза.

• Расслабьтесь. Поводите глазами вверх, вниз, влево, вправо.

• Откройте глаза.

• Потянитесь как маленькие котята.

• Улыбнитесь друг другу.

• И с хорошим настроением продолжим работу.

Стратегия «Мозговой штурм-Миға шабуыл -Brain storm»

Form the equations of the word problems on the picture

Task № 1: In a class of 20 students. 2 girls more than boys. How many girls and how many boys in the class?

Solution: Let x - the number of girls. y - the number of boys, then:

2 х = 22 х =11

у = 20 –х

у =9

Answer: (11;9)

Задание № 2.

Решение: Пусть х –кг граната водном мешке, у – кг малахита, тогда:

+

- у =-13 х =46-26

у = 13 х =20

Ответ: х=20; у=13

Если объединить два ответа, то у нас получится:11.09.2013

Стратегия «Мешочек заданий – қоржындағы тапсырмалар»

Учащиеся работают индивидуально, каждый выбирает одну из карточек,

и выполняют задание в тетради. Ученик, первым выполнивший определенное задание, подходит к учителю и объясняет идею решения, делает обоснования и выводы, учитель может задавать дополнительные вопросы, чтобы уточнить что-либо, отмечает сильные и слабые стороны его письменного решения и устного ответа, при необходимости дает ученику рекомендации. Нужно поощрять использование изученной лексики в устной речи и математических символов в записях

Группа А

За 1 плащ и 3 куртки пошло 9 м ткани,

а на 2 плаща и 5 курток – 16 м. Сколько ткани требуется на пошив плаща и сколько – на пошив куртки?

Группа В

Расстояние по реке между пунктами А и В туда и обратно катер проходит за 8 часов. Найдите это расстояние, если собственная скорость катера 8 км/ч, а скорость течения 2 км/ч?

Группа С

На рынке было закуплено 84 кг черешни и вишни, причем черешни куплено на 3 ящика меньше, чем вишни. Сколько ящиков черешни и вишни закуплено по отдельности, если в 1 ящике черешни 8 кг, а вишни 10 кг?

Задачник Мордкович 7 класс

Учебник Алгебра Макарычев 7 класс

Задачник Мордкович 7 класс

Учебник Алгебра Макарычев 7 класс

Задачник Мордкович 7 класс

Учебник Алгебра Макарычев 7 класс

Рефлексия 5мин

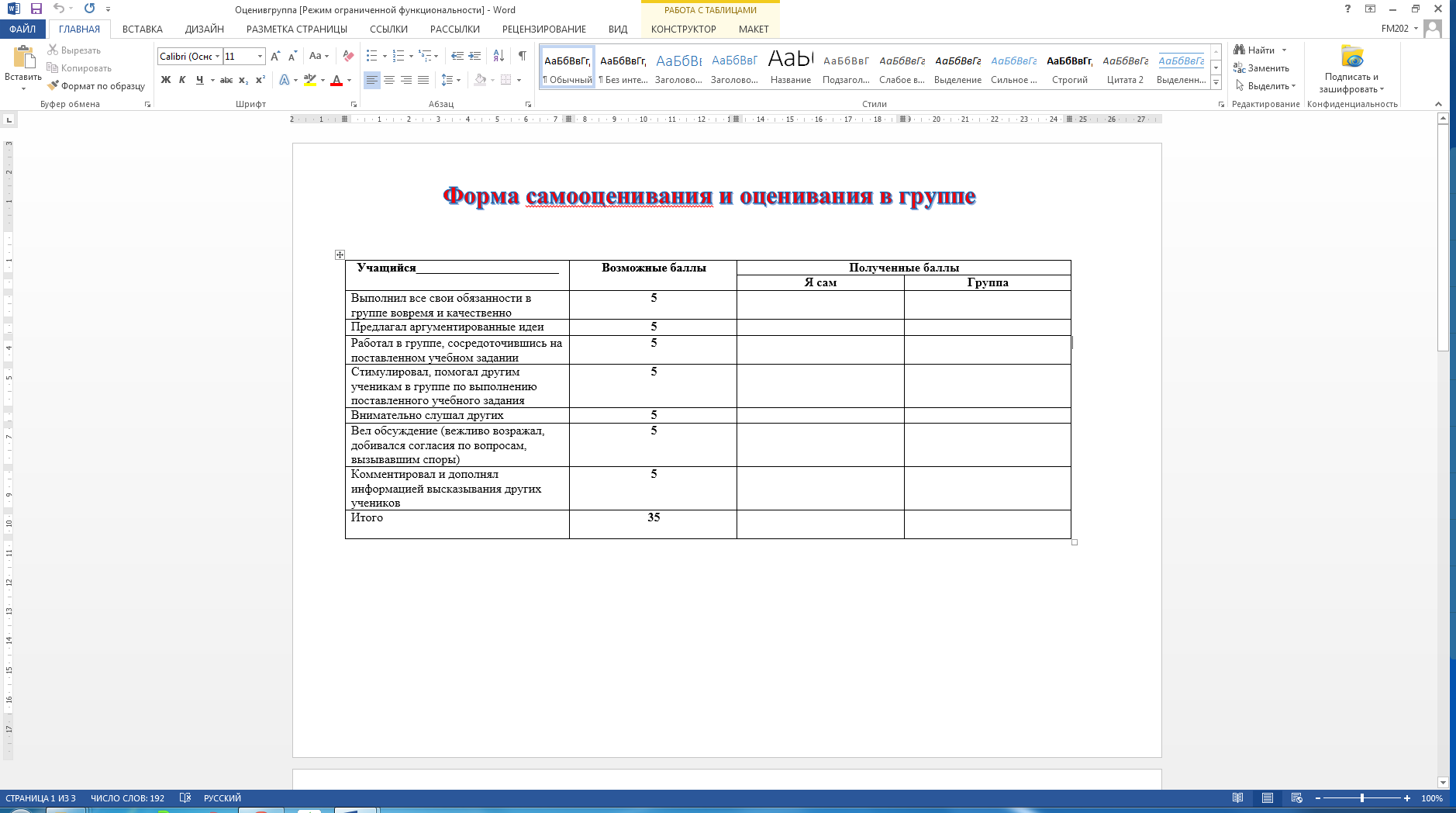
Вновь предложить вниманию учащихся слайд со списком целей обучения данной пары уроков. Сделать краткий обзор. Учащиеся проводят самооценивание своей работы в группе и консультант проводит оценивание работы всей группы.

Форма оценивания и самооценивания в группе

• Чему я научился на уроке?

• Над какими вопросами необходимо мне еще поработать?

 Как я участвовал в обсуждении задач?

Попросить учащихся высказаться по этому поводу.

Домашнее задание

Задача №1.Легковой автомобиль за 3,5 часа проехал то же расстояние,  что и грузовой за 5 часов. Найдите их скорости, если известно,  что легковой автомобиль двигался на 30 км/ч быстрее грузового.  

Задача №2.

Задача №2. В двух шкафах стояли книги. Если из первого шкафа переставить во второй 10 книг, то в обоих шкафах книг станет поровну. Если же со второго шкафа переставить в первый 44 книги, то в нем останется в 4 раза меньше книг, чем в первом. Сколько книг было в каждом шкафу?

Задание: Придумать или найти необычную задачу, которая решается с помощью системы уравнений, решить её и оформить все на альбомном листе.

Задачник Мордкович 7 класс

Учебник Алгебра Макарычев 7 класс

Ресурсы

• Задачник Мордкович 7 класс

• Учебник Алгебра Макарычев 7 класс

• https://ru.wikipedia.org/wiki/%D0%90%D1%82%D1%8B%D1%80%D0%B0%D1%83