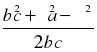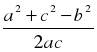Цель: научить обучающихся применять теоремы синусов и косинусов при решении задач.
Задачи:
общеобразовательная: закрепить знание учащимися теорем синусов и косинусов; научить применять эти теоремы в ходе решения задач по решению треугольников.
развивающая: развивать познавательный интерес обучающихся к геометрии; умение искать ответы на возникающие вопросы с помощью поставленных целей; умение видеть связь между геометрией и окружающей жизнью;
воспитательная: способствовать формированию целенаправленной деятельности учащихся через применение различных методов и форм обучения; воспитывать волю и настойчивость для достижения конкретных результатов.
МТО: Л.С. Атанасян учебник «Геометрия 7-9 классы», доска.
Просмотр содержимого документа
«Решение треугольников»
Формальная и содержательная часть урока
Урок № 9
«Решение задач по теме «Решение треугольников. Измерительные работы»
Цель: научить обучающихся применять теоремы синусов и косинусов при решении задач.
Задачи:
общеобразовательная: закрепить знание учащимися теорем синусов и косинусов; научить применять эти теоремы в ходе решения задач по решению треугольников.
развивающая: развивать познавательный интерес обучающихся к геометрии; умение искать ответы на возникающие вопросы с помощью поставленных целей; умение видеть связь между геометрией и окружающей жизнью;
воспитательная: способствовать формированию целенаправленной деятельности учащихся через применение различных методов и форм обучения; воспитывать волю и настойчивость для достижения конкретных результатов.
МТО: Л.С. Атанасян учебник «Геометрия 7-9 классы», доска.
Структура урока:
Организационный момент.
Актуализация опорных знаний и умений.
Контроль знаний – математический диктант.
Закрепление знаний с помощью решения задач.
Подведение итогов работы на уроке.
Задание на дом.
Начало урока.
Записать дату урока, тему урока. Сформулировать цель урока обучающимся (поставить наводящий вопрос: «Ребята, как вы думаете, чем сегодня мы будем заниматься на уроке?»)
Актуализация знаний:
| 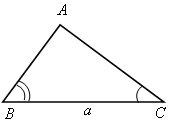
| ∟А, в, с | 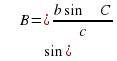
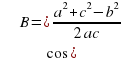
c = 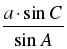
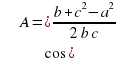 c =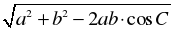 ; ;
∟В=180º- (∟А+∟С);
b = 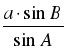 ; ;
∟C=180º- (∟А+∟B). |
| 
| ∟В, ∟А, с |
| 
| ∟А, ∟В, ∟С |
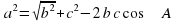
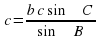
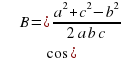
 с
с 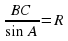
А
В
A
АВ=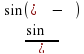
B
C D
Математический диктант
1 вариант. Дано: треугольник АВС, угол А=60º, угол С=30º, в = 10 см. Решить треугольник.
Проверка: угол В=90º, с=5 см, а=5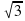 см
см
2 вариант. Дано: треугольник АВС, угол А=45º, в=4 дм, с=2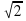 дм. Решить треугольник.
дм. Решить треугольник.
Проверка: а=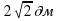 , угол С=45º, угол В=90º
, угол С=45º, угол В=90º
Решение задач.
№ 1026 – 1-я пара учащихся
№ 1027 – 2-я пара учащихся
Выполнить взаимопроверку.
| Карточка № 1 |
| 
| c =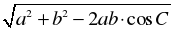 ; ; 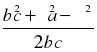
cos A =
 B = 180° – ( B = 180° – ( A + A +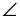 C) C)
|
| Дано: треугольник АВС, а=10 см, b = 5 см, 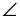 С = 30º С = 30º |
Карточка № 1 – выполняет учащийся 1
| Карточка № 2 |
| 
| 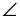 A = 180° – ( A = 180° – (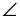 B + B +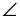 C); C);
b = 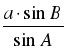 ; ;
c = 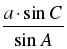 |
| Дано: треугольник АВС, а=10 см, 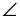 В = 60 º, В = 60 º, 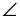 С = 30º С = 30º |
Карточка № 2 – выполняет учащийся 2
| Карточка № 3 |
| 
| 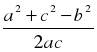
cos B =
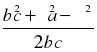
cos A =
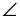 С = 180° – ( С = 180° – (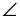 A + A +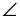 В) В)
|
| Дано: треугольник АВС, а=10 см, b = 6 см, с = 8 см |
Карточка № 3 – выполняет учащийся 3.
4 учащихся (которые слабо усвоили материал) – выполнить чертеж треугольника в тетради, указать элементы треугольника, которые нужно найти, записать теорему косинусов или синусов для решения задачи.
| Карточка № 4 |
| 
| Выполнить чертеж треугольника в тетради, указать 3 известных элемента треугольника, и 3 элемента треугольника, которые нужно найти, записать теорему косинусов или синусов для решения задачи. |
№ 1034 – у доски
Доп. задание № 1035
Подведение итогов урока.
- Что означают слова «Решить треугольник»?
- Можно ли определить высоту предмета, основание которого недоступно?
- Какие еще расчеты можно произвести при недоступности объекта?
- Какая часть урока вам больше всего запомнилась, а понравилась?
Выставление оценок учащимся.
Задание на дом № 1035, 1058(б), 1064* . Пояснение.
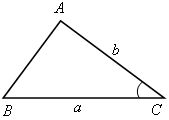
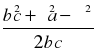
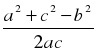

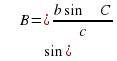
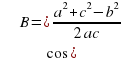
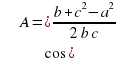


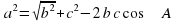
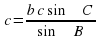
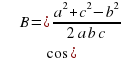
 с
с 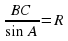

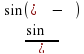
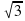 см
см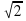 дм. Решить треугольник.
дм. Решить треугольник. 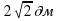 , угол С=45º, угол В=90º
, угол С=45º, угол В=90º