В данной разработке представлен урок геометрии в 9 классе по теме "Решение треугольников. Измерительные работы" с элементами технологии дифференцированного обучения. Цель урока: совершенствование навыков решения задач на решение треугольников; ознакомить учащихся с методами измерительных работ и показать применение теорем синусов и косинусов при их выполнении; активизировать познавательную деятельность учащихся на уроке; развивать умения размышлять, анализировать и делать выводы. Формы работы на уроке: фронтальная, индивидуальная, работа в дифференцированных группах.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока геометрии в 9 классе Решение треугольников. Измерительные работы.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока геометрии в 9 классе Решение треугольников. Измерительные работы.»
Полезное для учителя
Распродажа видеоуроков!
2000 руб.
2860 руб.
2000 руб.
2860 руб.
2020 руб.
2880 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
 ) В треугольнике АВС
) В треугольнике АВС 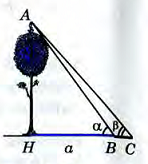 Найдите высоту дерева, если а=10м,
Найдите высоту дерева, если а=10м, 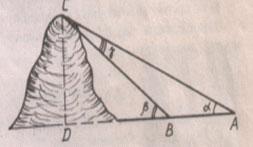

 А В
А В  А Дано:
А Дано:


 В
В  Дано:
Дано:
 Дано:
Дано:  Найти: АВ.
Найти: АВ.

 в
в  С
С















