Решение неравенств с двумя переменными

МБОУ «Зименковская СОШ»

Учитель математики Травова Т.М.

Решение неравенств с двумя переменными (Слайд 1)

Цель урока:

Ввести понятие неравенства с двумя переменными и составить алгоритм решения неравенств.

Задачи урока:

Формировать навыки решения неравенств.

Развивать критическое мышление и интерес к предмету у учащихся в процессе решения проблемных ситуаций и заданий творческого характера.

Учить анализировать, исследовать, делать выводы.

В ходе урока ученики закрепят свои знания о построении графиков, решении неравенств. Приобретут новые знания о решении неравенств с двумя переменными. Научатся находить верное решение, составлять алгоритм решения и пользоваться им при решении неравенств. Путем исследования обнаружат их некоторые свойства. Вся работа сопровождается слайдами. Применение ИКТ даст возможность провести урок оживленно, выполнить большой объем работы, со стороны ребят будет искренний интерес и эмоциональное восприятие.

Универсальные учебные действия, на формирование которых направлен образовательный процесс: умение работать в группе, развивать логическое мышление, умение анализировать, исследовать, делать выводы, отстаивать свою точку зрения. Обучить навыкам общения и сотрудничества. Использование данных технологий способствует развитию у обучающихся универсальных способов деятельности, опыта творческой деятельности, компетентности, коммуникабельности.

Ход урока:

1. Организационный момент.

Вступительное слово учителя.

На предыдущих уроках мы решали системы уравнений графическим способом, системы уравнений аналитическим способом. Сегодня мы переходим к изучению новой темы «Решение неравенств с двумя переменными» (Презентация) (Слайд 2). Для этого вспомним графики функций, которые вы изучали.

у = х²

у = 3х + 5

у = х3

у² + х² = 9

ху = 8

у = -2х

(х – 2)² + (у + 3)² = 16

2. Устная работа учащихся с использованием проектора.

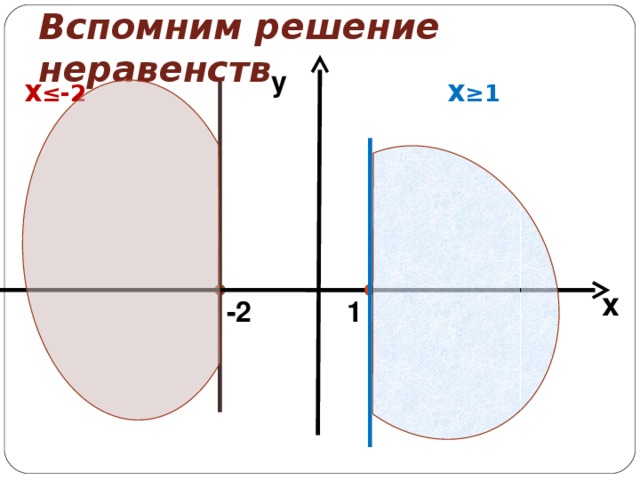
1) Х ≥ 1

2) X ≤ -2 (Слайд 3)

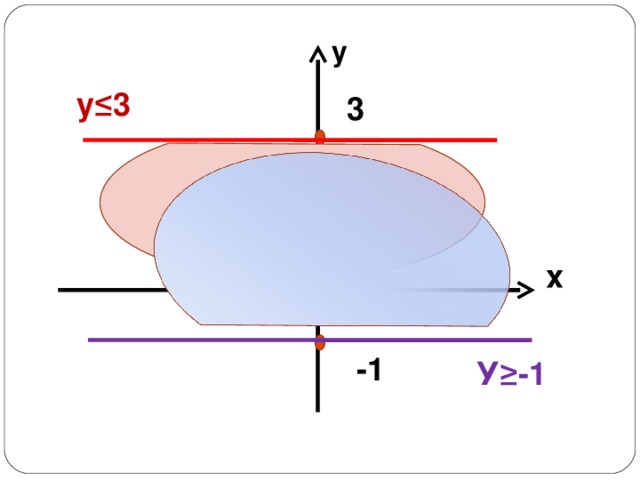
3) У -1

4) У

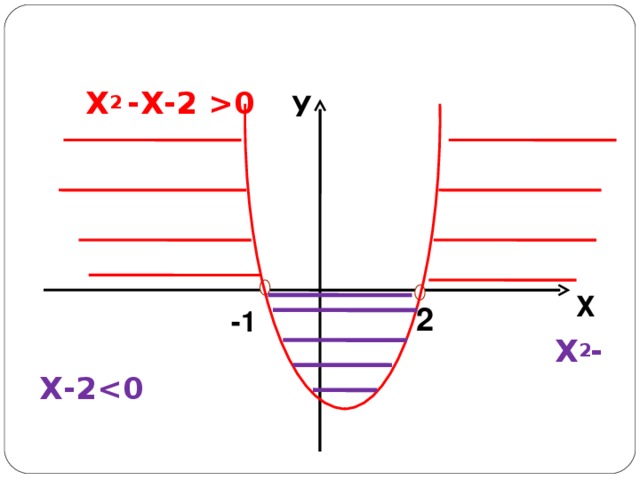
5) Х² – Х – 2 0

6) Х² – Х – 2

Как поступить, если даны функции с двумя переменными?

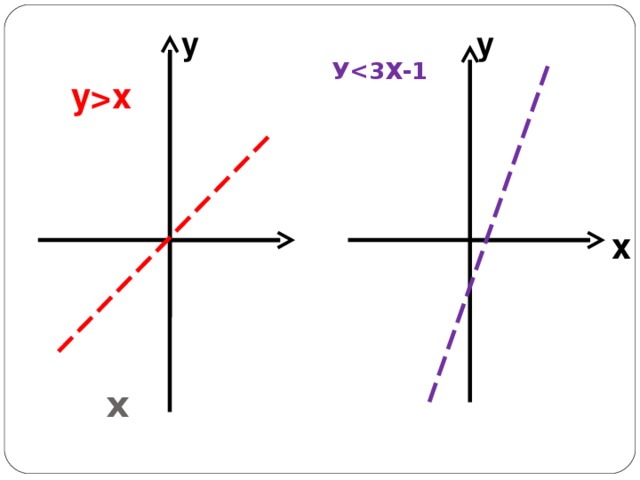
7) У Х

8) У

Какие графики они представляют? (Выслушиваются ответы учащихся.) Как можно найти решение?

3. Переходим к изучению новой темы «Решение неравенств с двумя переменными» (Слайд 6 - 7)

Запишите в тетрадях число, тему урока.

Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство (Слайд 8)

А если даны неравенства вида

2х+3у6(Слайд 9-12)

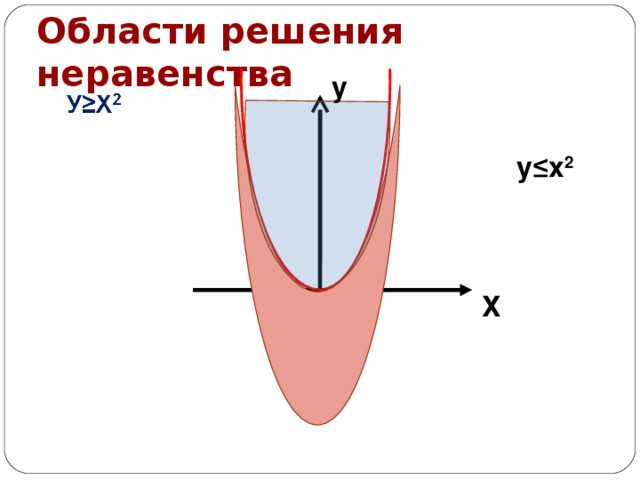
ух² - 1 (Слайд 13-15)

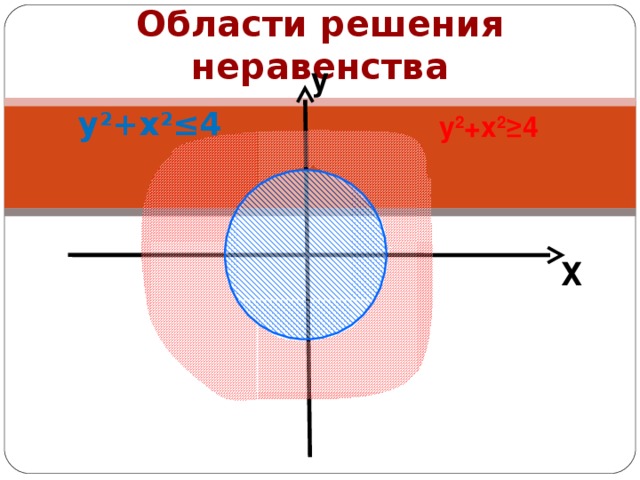
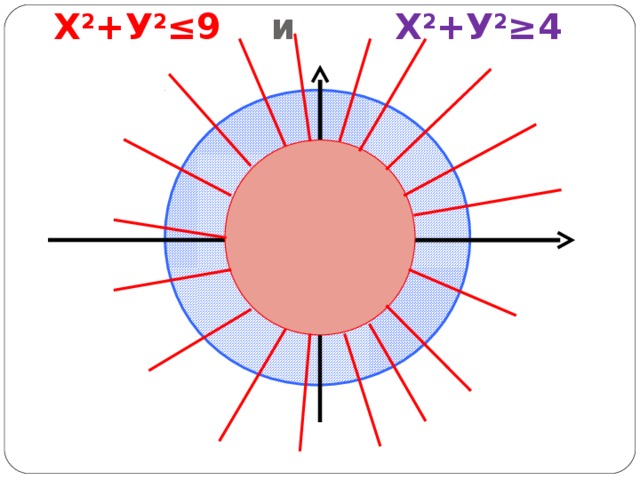
х² + у²

Ученики самостоятельно предлагают алгоритм решения неравенств (Слайд 18-20)

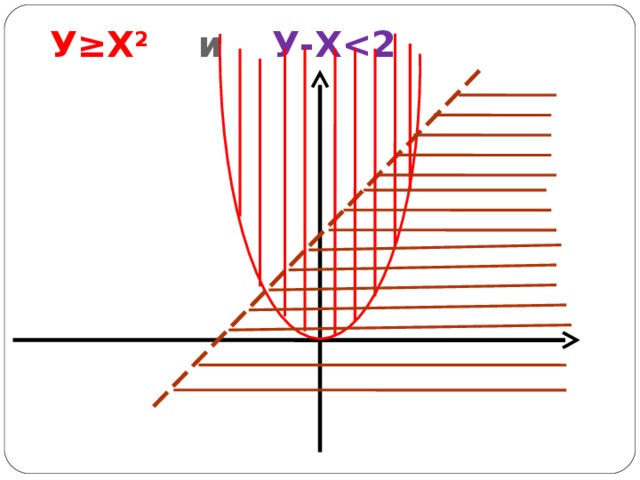
Если неравенство представлено в виде у f(x), то это неравенство задает на плоскости область, которая лежит не ниже графика.

Если неравенство представлено в виде уf(x),то это неравенство задает на плоскости область, которая лежит не выше графика.

Если линия f(x;у)– замкнутая, например окружность, или замкнутая ломанная?

Учащиеся предлагают следующее правило:

Если f(x;у)=0– замкнутая линия, то неравенство f(x;у)0, задает область, лежащую вне замкнутой линии, а неравенство f(x;у)

Учитель предлагает наиболее универсальное, полезное для проверки правило.

«Правило пробной точки» (Слайд 21)

1. Построить F(x;y) =0

2 .Взяв из каждой области пробную точку, установить, являются ли ее координаты решение неравенства.

3. Показать область решения неравенства.

4. Работа по учебнику: № 483 (а,г), № 487 (б).

5. Проверь себя У 2х – 1

У ² + 1

6. Подвести итоги урока, отметить наиболее активных учащихся, поставить оценки за урок. Поблагодарить учащихся за работу на уроке.

7. Домашнее задание (Слайд 22)

1. Придумать свое неравенство и изобразить на координатной плоскости множество его решений. Три разных задания.

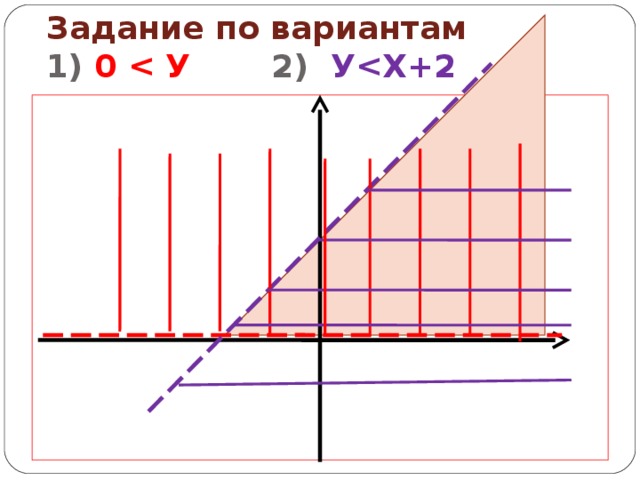
2. Построить в одной координатной плоскости множество решений неравенств

0 ≤ У

У ≤ -Х + 2

У ≤ Х + 2

Найти площадь и периметр полученной фигуры.

(Слайд 23)

Решение неравенств с двумя переменными

Урок алгебры

9 класс

Учитель математики

Травова Татьяна Михайловна

Повторим графики функций

У=Х 2 У=3Х +5 У=Х 3 У 2 +Х 2 =9 ХУ=8 У=-2Х (Х-2) 2 +(У+3) 2 =16

Вспомним решение неравенств

у

Х≤-2 Х ≥ 1

х

1

-2

у

у≤3

3

х

-1

У≥-1

0 Х 2 -Х-2 0 У Х 2 -1" width="640"

Х 2 -Х-2 0

Х 2 -Х-2 0

У

Х

2

-1

х х" width="640"

х

У 3Х-1

у

у

у х

х

Цели урока:

• Ввести понятие неравенств с двумя переменными
• Составить алгоритм решения неравенств
• Формировать навыки решения неравенств

Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство

Области решения неравенства

у

у≤х 2

Х

Области решения неравенства

у

у 2 +х 2 ≤4

у 2 +х 2 ≥4

Х

Правило пробной точки

1. Построить F(x ; y)=0

2.Взяв из каждой области пробную точку установить, являются ли ее координаты решением неравенства.

3.Показать область решения неравенства.

Задание по вариантам 1) 0 2) У

12

У≥Х 2 и У-Х

Х 2 +У 2 ≤9 и Х 2 +У 2 ≥4

2Х-1 У 2 (Х-1) 2 +(У+2) 2 ХУ8 3 У|Х| ХУ≥-10" width="640"

Проверь себя

1 2

У2Х-1 У 2 (Х-1) 2 +(У+2) 2 ХУ8 3

У|Х|

ХУ≥-10

Домашнее задание

1.Придумать свое неравенство и изобразить на координатной плоскости множество его решений. Три разных задания.

2.Построить в одной координатной плоскости множество решений неравенств

0 ≤ У У ≤ -Х+2 У ≤ Х+2

Найти площадь и периметр полученной фигуры.

Спасибо за урок