| 2. Актуализация теоретических знаний и фиксирование индивидуального затруднения в пробном учебном действии (4-5 мин). Открываем тетради, записываем число, оставьте место под тему урока. Мы запишем её позже. -Давайте с вами вспомним, чем мы занимались на прошлом уроке. -Правильно, поэтому я предлагаю вам решить следующие неравенства, устно проговаривая алгоритм решения. (слайд 3) Решить неравенства: x2-2x-80 Цель задания: вспомнить алгоритм решения квадратичного неравенства - Что мы делаем на первом шаге?
-Что можно сказать про эту функцию?
-Правильно, следующий шаг?
|
-учащиеся открывают тетради, записывают число
-решали квадратичные неравенства
-записывают решение неравенств в тетрадях, устно проговаривая алгоритм решения
-Рассматриваем квадратичную функцию 1. y= x2-2х -8 -её графиком является парабола, ветви которой направлены вверх
-Решаем квадратное уравнение 2. x2-2x-8=0 - По теореме Виета- |
| -Как можно решить данное уравнение? -Проговорите, пожалуйста, решение.
-Молодцы, что мы делаем на третьем шаге
-Точки будут закрашенные или выколотые и почему?
-Дальше что делам? -Промежутки с какими знаками запишем в ответ и почему? -Числа -4 и 2 включаем или нет? -Правильно, молодцы, продиктуйте ответ. -У кого есть вопросы по решению данного неравенства?
-Следующее неравенство (слайд 4) (x-2)(x+3) 0 Цель задания: подготовить учащихся к изучению новой темы – вспомнить разложение квадратного трехчлена на множители -Как можно решить данное неравенство?
- Правильно, решаем.
-Записываем квадратичную функцию 1) y= x2+x-6, -Что про неё можно сказать? -Ребята, обратите внимание на подчеркнутые выражения, что мы с вами получили? - Значит, что можно сразу найти? -Записываем квадратное уравнение и его корни 2) x2+x-6=0 x1=2, x2=-3 -Дорешайте самостоятельно это неравенство
Какой ответ получили? - Давайте проверим (на слайде появляется решение неравенства) 3. Выявление места и причины затруднения. А теперь решим следующее неравенство (слайд 5) (x-2)(x-3)(х-4) ˃0 Цель задания: показать актуальность изучения новой темы путем создания проблемной ситуации.
- Ребята, сможем ли мы решить данное неравенство предыдущим способом? - Давайте попробуем выяснить где именно возникло затруднение и почему?
- Действительно, данное неравенство можно решить методом интервалов, наиболее удобным и универсальным способом решения любых неравенств. - Сформулируйте тему нашего урока
4. Постановка учебной задачи (4-5 мин). Цели для учителя: -создание условий для постановки учебной задачи. Для учащихся: -выявление места и причины затруднения, постановка цели урока
-Что нужно сделать, чтобы преодолеть возникшее затруднение?
- Какая же будет цель нашей деятельности на уроке сегодня? Цель урока: выработать алгоритм решения неравенств методом интервалов и рассмотреть его применение на примерах. 5. «Открытие» учащимися нового знания. (7-8 мин). Цели для учащихся: -выбор способа решения учебной задачи; -выдвижение и обоснование гипотезы. Для учителя: - фиксирование в речи и знаково нового способа действий. - Для того чтобы решить данное неравенство, мы с вами, как и в предыдущих случаях, должны решить соответствующее уравнение (слайд 7) 1.(х-2)(х-3)(х-4)=0 -Как решается данное уравнение ?
3. Отмечаем полученные корни на оси ОХ, какие будут точки? Полученные корни разобьют ось ОХ на числовые промежутки, назовите их
    3 4 2 X
4. Заполняем таблицу, где указываем знак каждого множителя выражения на рассматриваемых промежутках. Для этого из каждого промежутка берем произвольное число, и подставляем в множитель. Знак полученного числа заносим в таблицу
5.Далее на числовой оси расставляем знаки многочлена ( произведение знаков трех множителей на каждом промежутке) 6. Так как знак неравенства « », то выбираем промежутки со знаком «+ », если бы был знак неравенства « Ответом будет объединение этих промежутков -С помощью данного метода можно решить неравенство любой степени, в том числе и второй, которые мы с вами решали с помощью схематического построения параболы. - У вас на столах лежат памятки, которые вы вклеите в свои тетрадки для теории. В этой памятке приведен алгоритм решения неравенств с помощью метода интервалов в общем виде. -Давайте с вами прочитаем этот алгоритм (Слайд 8) Физкультминутка | 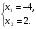 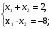
- Отмечаем полученные корни на оси Ох и через отмеченные точки схематично строим график параболы -выколотые, потому что знак неравенства строгий
3. 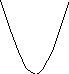 + - + + - +
   -4 2 Х -4 2 Х
- Расставляем знаки на промежутках - Промежутки со знаком +, потому что в неравенстве стоит знак -Нет, потому что знак неравенства строгий 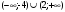 -Ответ: -Ответ:
(задают, если есть, вопросы)
« Круг идей» - ученики выдвигают гипотезы -если мы раскроем скобки, то получим квадратное неравенство и решим его, аналогично предыдущему примеру.
(у доски решает один ученик) -(x-2)(x+3)= x2+3x-2x-6= x2+x-6
- её графиком является парабола, ветви которой направлены вверх - Разложение квадратного трехчлена на множители
-Корни квадратного уравнения
(записывают решение неравенства в тетради)
(зачитывают свой ответ)
(самопроверка)
-нет,
-потому, что после раскрытия скобок мы получаем неравенство третьей степени, а мы умеем решать только линейные и квадратичные.
« Решение неравенств методом интервалов»
- изучить метод интервалов и научиться применять его для решения неравенств.
- выработать ( сформулировать) алгоритм решения неравенств методом интервалов.
Учащиеся отвечают на вопросы учителя и работают с карточками « Заполни пропуски»
x-2=0 x-3=0 x-4=0 x=2 x=3 x=4
(-;2) (2;3) (3;4) (4;+)
|
| (-;2) | (2;3) | (3;4) | (4;+) | | x-2 x-3 x-4 | - - - | + - - | + + - | + + + |
    + 3 4 2 - _ + X
Ответ: (2;3)(4;+)
Читают алгоритм |
| 5. Первичное закрепление (4-5 мин). Цели для учителя: -создание условий для первичного закрепления. Для учащихся: -усвоение нового способа действий. -Нам надо решить неравенства методом интервалов. Кто хочет рассказать, как это надо сделать? Первое неравенство (х+3)(х-4)(х-7) 0.
Второе неравенство (х2-9)(х+5) ≤ 0.
6. Самостоятельная работа в парах в взаимопроверкой по эталону (4-5 мин). Цели для учителя: -создание условий для интериоризации (переход извне внутрь) нового способа действий; -создание ситуации успеха. Для учащихся: -индивидуальная рефлексия достижения цели.
7. Включение в систему знаний и повторение (7-8 мин). Цели для учителя: -создание условий для включения «открытия» в систему знаний, повторение и закрепление ранее изученного. Для учащихся: -включение «открытия» в систему знаний, повторение и закрепление ранее изученного. - А сейчас, я предлагаю разобрать задания, где пригодятся полученные сегодня знания. Разбейтесь на 4 группы ( по геометрическим фигурам, лежащим у каждого на парте ) - Оцените свою работу в группе по 5-ой шкале.
8. Рефлексия учебной деятельности на уроке (итог урока) (2-3 мин). Цели для учителя: -создание условий для рефлексии учебной деятельности учащихся на уроке. - И вспомним начало нашего урока. Удалось ли нам достигнуть поставленных целей? С каким новым методом решения неравенств мы сегодня познакомились? -Какова была цель сегодняшенего урока? -Как вы думаете, мы достигли поставленной цели? -Неравенства какой степени мы теперь можем решать? - Ян Амос Коменский говорил: «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию». Я надеюсь, что в сегодняшнем уроке вы найдете для себя хоть крупинку полезного.
У каждого из вас на столе мишки. Уходя из класса, прикрепите на доску одного из них. Мишка зеленого цвета обозначает: “Я удовлетворён уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке”. Мишка желтого цвета обозначает: “Урок был интересен, я принимал в нём активное участие, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно”. Мишка розового цвета обозначает: “ Я получил пользу от урока, но мне не все удалось выполнить правильно, домашнее задание я выберу среднего уровня 9. Домашнее задание ( 2 мин) Ваше домашнее задание нескольких уровней. Каждый выбирает уровень себе по силам.

|
« Обучая - учусь»
Решение: 1. Найти корни уравнения - x1=-3, x2=4, x3=7, - 2.Отметить на числовой прямой корни -выколотые - 3.Определить знак выражения на каждом из получившихся промежутков - Определить знак каждого множителя на каждом из промежутков (чертят таблицу знаков) (диктует знаки) - 4. Записать ответ, выбрав промежутки с соответствующим знаку неравенства знаком -промежутки со знаком +, потому что знак неравенства 0 Ответ: (-3;4) 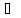 (7; +∞). (7; +∞).
Учащиеся решают самостоятельно, с последующей взаимной проверкой по эталону ( Слайд 9) Ответ: (-∞;-5] 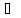 [-3;3]. [-3;3]. « Тайный конверт» Каждая пара получает закрытый конверт с заданием, аналогичным одному из рассмотренных примеров и решает поставленную задачу, а затем выполняется самопроверка работы по образцу – ( слайд 10) Задания: 1) (х + 7)(х + 2)(4 – х)(2х – 10) ≥ 0. ( x Є [-7; -2] U [4; 5] ) 2) (х + 2)(х2 – 9) (х Є (- ∞; -3) U (-2; 3) ) 3) (х2 + 4х – 5)(х+7)(х + 3) ≥ 0 (х Є (- ∞; -7] U [-5; -3] U [1; + ∞) ) 4) (х + 4)(х + 1)(х – 1)(х – 8) ≥ 0 (х Є (- ∞; - 4] U [-1;1] )
« Работа в группах» Задание для групп № 1,2: № 332 (а) № 335(а) Задание для групп № 3,4: № 332 (б) № 335 (б)
- Методом интервалов
- Научиться решать неравенства методом интервалов
- Да
- Неравенства любой степени
Решить неравенства методом интервалов Средний уровень 1) х2 – 7х + 12 ≤ 0 2) (х + 10)(х – 4) 3) 2х (8 + х)(х – 12) 0 4) (х + 2)(7 – х)(х – 13) 0 5) (х + 5)/(х - 6) 0 Достаточный уровень 1) (х – 2)(х +5)/(х + 2) ≥ 0 2) (х + 3)2(х + 1)(х – 2) ≤ 0 3) (16 – х2)(3х2 + 1) 0 4) (6 – 3х)/(х + 4) ≥ 0 Высокий уровеь 1) (х4 – 16х2)( - х2 – 5) ≤ 0 2) (– х2 + 8х – 7)/(х2 + х – 2) 0 3) х3 – 5х2 + 6х ≥ 0 4) (х – 2)(х + 2)2(х + 3)/(х - 1) ≤ 0
|



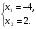
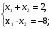
 + - +
+ - +

 -4 2 Х
-4 2 Х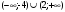 -Ответ:
-Ответ:
 (7; +∞).
(7; +∞). 


















