Действия над комплексными числам
"Комплексное число –
это тонкое и поразительное средство божественного духа,
почти амфибия между бытием и небытием".
Г. Лейбниц
Цели урока: познакомить учащихся с историей комплексных чисел; формировать навыки выполнения алгебраических действий над комплексными числами;
развивать мыслительную деятельность учащихся; развивать интерес к предмету через включение в план урока исторического материала;
воспитывать способность подходить к изучаемым проблемам с позиции исследователя.
Тип урока: усвоение новых знаний
Оборудование: опорный конспект, презентация
Ход урока
І. Организационный момент
ІІ. Проверка домашней работы
IІІ. Актуализация опорных знаний
ІV. Изучение нового материала
Сложение комплексных чисел определяется правилом:
(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2 ) + (b 1 + b 2 ) i .
Умножение комплексных чисел определяется правилом:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2 ) + (a 1 b 2 + a 2 b 1 ) i .
Пример . Даны комплексные числа z 1 = 2 + 3i , z 2 = 5 – 7i .
Найти:
а) z 1 + z 2 = …= 7 – 4i ; б) z 1 – z 2 = …= – 3 + 10i ;
в) z 1 z 2 = (2 + 3i )(5 – 7i ) = 10 – 14i + 15i – 21i 2 = 10 – 14i + 15i + 21 = 31 + i
(здесь учтено, что i 2 = – 1).
Пример . Выполнить действия:
а) (2 + 3i )2 = 4 + 2×2×3i + 9i 2 = 4 + 12i – 9 = – 5 + 12i ;
б) (3 – 5i )2 = 9 – 2×3×5i + 25i 2 = 9 – 30i – 25 = – 16 – 30i ;
в) (5 + 3i )3 = 125 + 3×25×3i + 3×5×9i 2 + 27i 3 ;
так как i 2 = – 1, а i 3 = – i , то получим (5 + 3i )3 = 125 + 225i – 135 – 27i = – 10 + 198i .
Рассмотрим теперь применение формулыa + b )(a – b ) = a 2 – b 2 . (*)
Пример . Выполнить действия:
а) (5 + 3i )(5 – 3i ) = 52 – (3i )2 = 25 – 9i 2 = 25 + 9 = 34;
б) (2 + 5i )(2 – 5i ) = 22 – (5i )2 = 4 + 25 = 29;
в) (1 + i )(1 – i ) = 12 – i 2 = 1 + 1 = 2.
- Определение. Два комплексных числа называются сопряженными , если они отличаются друг от друга только знаками перед мнимой частью.
Пример . Выполнить деление:
Произведем умножение для делимого и делителя в отдельности:
(2 + 3i )(5 + 7i ) = 10 + 14i + 15i + 21i 2 = – 11 + 29i ;
(5 – 7i )(5 + 7i ) = 25 – 49i 2 = 25 + 49 = 74.
Итак,
Пример . Решите уравнение:
а) x 2 – 6x + 13 = 0; б) 9x 2 + 12x + 29 = 0.
Решение. а) Найдем дискриминант по формулеD = b 2 – 4ac .
Так как a = 1, b = – 6, c = 13, то D = (– 6)2 – 4×1×13 = 36 – 52 = – 16;
Корни уравнения находим по формулам
б) Здесь a = 9, b = 12, c = 29. Следовательно, D = b 2 – 4ac =122 – 4×9×29 = 144 – 1044 = – 900,
Находим корни уравнения:
Действия над комплексными числами в тригонометрической форме.
1) Умножение.
Пусть два числа заданы и в алгебраической и в тригонометрической формах:
z 1 = a 1 + b 1 i = r 1 (cos φ 1 + i sin φ 1 ) , z 2 = a 2 + b 2 i = r 2 (cos φ 2 + i sin φ 2 ) .
На основании исходного определения правила умножения и формулы косинуса и синуса суммы получаем:
z 1· z 2 = r 1 · r 2 (cos ( φ 1 + φ 2 ) + i sin ( φ 1 + φ 2 )); r 1 · r 2 0 .
Пример. Найти произведение чисел z 1 = 2 cos 50º + 2 i sin 50º , z 2 = cos 40º + i sin 40º .
Решение. Тригонометрические формы этих чисел имеют вид:
z 1 = 2 · (cos 50º + i sin 50º), z 2 = 1· (cos 40º + i sin 40º).
Тогда z 1 · z 2 = 1· 2 · (cos (50º + 40º) + i sin (50º + 40º)) = 2(cos 90º + i sin 90º) = 2(0 + i) = 2i.
2) Деление комплексных чисел в тригонометрической форме.
Деление в поле комплексных чисел на числа, отличные от нуля, всегда выполнимо. Если числа z 1 z 2 заданы в тригонометрической форме
z 1 = r 1 ( cos φ 1 + i sin φ 1 ), z 2 = r 2 ( cos φ 2 + i sin φ 2 ) , причем z 1 ≠ 0 , то
[cos (φ 2 - φ 1 ) + i sin (φ 2 - φ 1 )]
Пример. Найти частное чисел z 1 = 2 cos 50º + 2 i sin 50º , z 2 = cos 40º + i sin 40º .
Решение. Тригонометрические формы этих чисел имеют вид:
z 1 = 2 · (cos 50º + i sin 50º), z 2 = 1· (cos 40º + i sin 40º).
Тогда (cos (50º - 40 º) + i sin (50º - 40º)) = 2(cos 10º + i sin 10º) .
V. Формирование умений и навыков
Произведите сложение и вычитание комплексных чисел:
1) (3 + 5i ) + (7 – 2i ). 2) (6 + 2i ) + (5 + 3i ). 3) (– 2 + 3i ) + (7 – 2i ). 4) (5 – 4i ) + (6 + 2i ). 5) (– 5 + 2i ) + (5 + 2i ). 6) (– 3 – 5i ) + (7 – 2i ).
Произведите умножение комплексных чисел:
9) (2 + 3i )(5 – 7i ). 10) (6 + 4i )(5 + 2i ).i )3i . 16) (2 – 3i)(– 5i).
Выполните действия:
17) (3 + 5i )2 . 18) (2 – 7i )2 .i )3 . 23) (4 + 2i )3 .
25) (3 + 2i )(3 – 2i ). 27) (1 – 3i )(1 + 3i ). i )(7 + 6i ). 29) (a + bi )(a – bi ).
Решите уравнения:
32) x 2 – 4x + 13 = 0. 33) x 2 + 3x + 4 = 0. Подведение итогов урока.
«Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной законченностью». Симон Стевин
VII. Домашнее задание
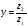 =
= 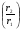 [cos (φ2 - φ1) + i sin (φ2 - φ1)]
[cos (φ2 - φ1) + i sin (φ2 - φ1)]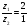 (cos (50º - 40 º) + i sin (50º - 40º)) = 2(cos 10º + i sin 10º).
(cos (50º - 40 º) + i sin (50º - 40º)) = 2(cos 10º + i sin 10º).















