Разработка открытого урока по теме Решение показательных уравнений

Решение примеров на закрепление данной темы

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Урок МОЙ Логарифмические уравнения _по группам»

Открытый урок по теме "Решение логарифмических уравнений".

Тип урока: комбинированный.

Цели урока:

Дидактическая:

1) продолжить формирование ЗУН при решении логарифмических уравнений;

2) систематизировать методы решения логарифмических уравнений;

3) учить применять полученные знания при решении заданий повышенной сложности;

4) совершенствовать, развивать и углублять ЗУН по данной теме;

Развивающая:

1) развивать логическое мышление, память, познавательный интерес;

2) формировать математическую речь;

3) вырабатывать умение анализировать и сравнивать;

Воспитательная:

1) воспитывать аккуратность при оформлении сложных задач, трудолюбие;

2) воспитывать умению выслушивать мнение других.

3) воспитывать самостоятельность при выборе жизненного пути, будущей профессии.

Оборудование: персональный компьютер, мультимедийный проектор, экран,

№	Этап урока	Задача этапа	Деятельность учителя	Деятельность учащихся	Результат деятельности учащихся
1	Деление на группы (5 мин)	Подготовка к уроку.	Студенты рассаживаются на три группы по 4-5 чел.	Придумывают название. Распределяют роли: Руководитель, арбитр, эрудит, счетчик.	Настраиваются на работу в группе.
1	Повторение пройденного (8 мин)	Проверка усвоения знаний	Задаю вопросы руководителю группы ( он решает кто отвечает) 1.Дать определение уравнения 2.Что такое корень уравнения? 3. Что такое область определения уравнения? 1.Что значит решить уравнение? 2. Что такое корень уравнения? 3. Дать определение логарифма. 4. Какие уравнения называют логарифмическим?	Руководитель группы решает кто отвечает на вопросы. Счетовод отмечает правильные ответы.	Отметка за работу
3.	Изучение нового материала Групповая работа. (15 мин.)	Самостоятельное изучение метода решения логарифмического уравнения.	Группы получают задание по выбору , на основании опорного конспекта, изучают : 1. метод решения с помощью определения; 2. метод потенцирования; 3. метод введения вспомогательной переменной	Пишут дату и тему урока. Решают задачи.	Систематизация опорных знаний Запись итогов обсуждения в заранее заготовленную таблицу.
5	Обмен полученными знаниями . межгрупповая работа (20 мин.)	Выяснить степень усвоения знаний.	Репродуктивный метод. Проверяет правильность решения и понятого метода.	Эрудит решает задачу по изученному методу. Арбитр рассказывает действия решения. Другие группы записывают в тетрадях и задают вопросы.	Каждая группа защищает свой метод у доски, давая объяснения решения. Таким образом, изучаются все три метода.
6.	Закрепление материала (10 мин)	Самостоятельная работа групп.	Каждая групп получает задание не своего метода и решает его.	Группы решают самостоятельно задания . проверяют правильность решения третья группа и ставит баллы.	Счетовод подводит итого. Каждая группа изучает все три метода.
6	Итог урока (20мин)		Каждая группа подготовила доклад с презентацией на вопрос «Зачем нужны логарифмы?»	Члены группы рассказывают и показывают презентацию.	Расширяют знания.
7	Завершение урока.	Рефлексия в виде синквейна.	Предлагает составить синквейн на слова Логарифм, уравнение.	Составляют синквейн Логарифм Натуральный, десятичный Вычисляет, упрощает, уравнивает Логарифмирование – вычисление логарифма Просто как дважды два Уравнение Квадратное, линейное Разыскивает, находит, выполняет Помогает нам решать сложные задачи Равенство	Подводят итоги в виде рефлексии.
	Домашнее задание (2мин)		Запись на доске.	Записывают в дневник.

Просмотр содержимого документа
«карта для групп»

Карточки для групп

Метод решения с помощью определения;

Метод потенцирования;

Метод введения вспомогательной переменной

log ² ₂ x - 4log² x + 3 = 0

Просмотр содержимого документа
«опорный конспект»

Опорный конспект

Фронтальный опрос

Дать определение уравнения	Равенство, содержащее переменную, называется уравнением.
Что значит решить уравнение?	Решить уравнение - значить найти его корни или доказать, что корней нет.
Что такое корень уравнения?	Значение переменной, при которой уравнение обращается в верное равенство, называется корнем уравнения.
Что такое область определения уравнения?	Областью определения уравнения называется множество значений переменной уравнения f(x)=g(x), при которых одновременно имеют смысл f(x) и g(x).
Какие уравнения называются равносильными?	Уравнения, имеющие одинаковые корни или не имеющие корней называются равносильными.
Следствия равносильности	Если к обеим частям уравнения f(x)=g(x) прибавить одну и ту же функцию у(х) определенную при всех значениях переменной из области определения данного уравнения, то уравнение f(x)+ у(х) =g(x)+у(х) равносильно данному. Если к оби части уравнения f(x)=g(x) умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение равносильное данному.
Что такое логарифм?	Логарифмом положительного числа b по основанию a (а0, a) называется показатель степени Х, в которую нужно возвести а, чтобы получить b, т. е
Какое уравнение называется логарифмическим?	Уравнение, в котором переменная находится под знаком логарифмической функции.

Свойства логарифмов

При решении логарифмических уравнений применяются следующие методы:

Решение уравнений, основанное на применении определения логарифма.
Применение основного логарифмического тождества.
Решение с помощью потенцирования.
Введение новой переменной.
Использование логарифмирования.
Переход к логарифму с новым основанием.

( При решении логарифмических уравнений необходима проверка все найденных корней или нахождения области определения уравнения, т.е. соблюдение равносильных переходов)

Метод, основанный на определении логарифма .

По определению логарифма имеем:

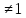
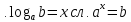
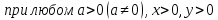
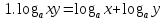
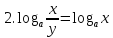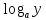
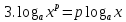
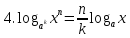
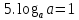
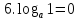
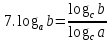
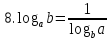
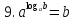
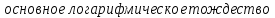
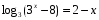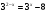, то есть 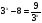(свели уравнение к показательному уравнению, которое решается методом введения нового неизвестного),

Следовательно .

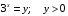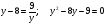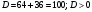: 2 корня, по обратной теореме Виета имеем: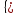_{,следовательно}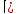

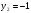- не удовлетворяет условию .

Имеем: .

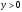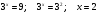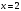Проверка: если , тогда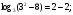

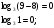
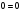– верно.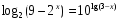

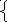
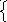
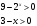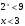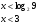Ответ: .

Применение основного логарифмического тождества

Найдем ОДЗ:

; ; , следовательно .

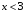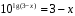Применив в правой части основное логарифмическое тождество, получим:

, следовательно, уравнение примет вид:

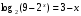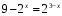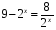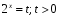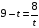
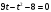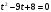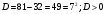Используя определение логарифма, получаем:

;

Пусть , имеем:

;

следовательно, 2 корня

; .

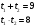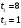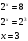или .

Но не входит в ОДЗ, следовательно, это посторонний корень.

Ответ: .

Метод, использующий монотонность логарифмической функции (метод потенцирования).

Для каждой монотонной функции из равенства следует, что .

Рассмотрим уравнение вида при решением этого уравнения будут все те решения уравнения , для которых (или ).

Поэтому уравнение можно решить по алгоритму:

Найти ОДЗ уравнения;
Решить на ОДЗ этого уравнения равносильное ему уравнение .

Конечно, не все уравнения будут иметь вид _, поэтому необходимы будут преобразования, используя свойства логарифмической функции.

Так как , то ; _, получаем .

Исходное уравнение, используя свойства логарифмической функции можно представить в виде:

данное уравнение при равносильно уравнению:

Возведем в квадрат, получим

следовательно, уравнение имеет два корня:

, так как , то посторонний корень.

Ответ: .

Замечание: переход от равенства к равенству называется потенцированием по основанию при . Совершая потенцирование мы совершаем переход, не являющийся равносильным, поэтому нужна проверка.

Введение нового неизвестного

ОДЗ .

Пусть , тогда

по обратной теореме Виета получаем:

; .

или .

Оба корня входят в ОДЗ.

Ответ: 10; 10000.

Применение логарифмирования.

Логарифмирование по основанию представляет собой переход от равенства к равенству , для этого .

Решим уравнение .

Уравнение содержит неизвестную величину, как в основании, так и в показателе степени, его можно решить, логарифмируя левую и правую часть по основанию 10, так как в условии уже имеется десятичный логарифм. Получаем:

, где .

Введем новую переменную и учитывая, что получаем:

или .

Вернемся к замене:

или

Оба корня удовлетворяют ОДЗ. Все преобразования были тождественны, следовательно, оба корня являются решение уравнения.

Ответ: .

Переход к логарифму по новому основанию

Найдем ОДЗ:

; , следовательно, .

Перейдем в уравнении к логарифму по основанию 3, получим:

, следовательно,

Введем новое неизвестное , получаем:

, что тождественно

, следовательно, 2 корня.

; .

Получаем:

или

Оба корня больше -1 и не равны нулю, то есть входят в ОДЗ.

Ответ: ; 8.

Учимся на чужих ошибках.

Решить уравнение

Решение: логарифмируем обе части уравнения по основанию 3.

Ответ: .

Приведенное решение не верно. Логарифмировать данное уравнение нельзя, так как выражение . Функция в левой части уравнения принимает только положительные решения, поэтому исходное уравнение решений не имеет.

Ответ: решений нет.

Решить уравнение .

Используя свойства логарифмов, имеем:

Ответ: 0; 4.

Приведенное решение не верно, так как нет проверки или оценки ОДЗ. является посторонним корнем.

Ответ: 4.

Решить уравнение

, что тождественно ;

Ответ: 5.

Решение не верно, так как нет проверки и нарушена операция потенцирования. Верный ответ .

Решить уравнение

; ;

;

Ответ: .

Решение не верно, так как не учтено условие , исходя из которого , следовательно корень не входит в ОДЗ.

Ответ: .

Просмотр содержимого презентации
«Решение лог уравнений»

РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ

Цели урока:

Обобщить и систематизировать изученные методы решения логарифмических уравнений
Выявить особенности каждого метода
Выяснить, всегда ли логарифмические уравнения решаются одним из изученных нами методом

Методы решения логарифмических уравнений:

По определению
Метод потенцирования
Метод замены переменной
Метод логарифмирования

Разбить уравнения на группы по методу их решения:

10.

11.

12.

Разбить уравнения на группы по методу их решения:

По определению

Метод замены переменной

10.

Метод потенцирования

11.

Метод логарифмирования

12.

Метод потенциирования:

1. Определить ОДЗ уравнения (подлогарифмические выражения положительны);

2. Пропотенцировать обе части уравнения по основанию равному основанию логарифма;

3. Перейти к равенству подлогарифмических выражений, применив свойство логарифма;

4. Решить уравнение и проверить полученные корни по ОДЗ;

5. Записать удовлетворяющие ОДЗ корни в ответ.

Признак: уравнение может

быть представлено в виде

равенства двух логарифмов

по одному основанию .

Метод замены переменной:

1. Определить ОДЗ уравнения (подлогарифмические выражения положительны);

2. Произвести замену переменной;

3. Решить полученное уравнение;

4. Составить простейшие логарифмические уравнения, возвращаясь к первоначальной переменной;

5. Проверить полученные корни по ОДЗ;

6. Записать удовлетворяющие ОДЗ корни в ответ.

Признак: Все логарифмы

в уравнении могут быть

сведены к одному и тому же

логарифму, содержащему

переменную.

Метод логарифмирования:

Определить ОДЗ уравнения (подлогарифмические выражения положительны);
Прологарифмировать обе части уравнения по основанию равному основанию логарифма в показателе степени;
Вынести показатель степени за знак логарифма, пользуясь свойством логарифма;
Решить полученное уравнение, пользуясь методом замены переменной.

Признак: переменная

содержится и в основании

степени, и в показателе

степени под знаком

логарифма.

Комбинированные уравнения:

№

Уравнение

Методы

ЗП, ЛГ

Решение этого уравнения…

Комбинированные уравнения:

При заполнении последней графы

таблицы используйте следующие

обозначения:

«+» – всё понятно (2 балла) ;

«?» – понятно, но остались вопросы

(1 балл) ;

«-» – ничего не понятно (0 баллов) .

Задание части С5 теста ЕГЭ:

При каких значениях параметра а уравнение

имеет решения на промежутке [8;9)?

План решения:

Исследовать ОДЗ уравнения;
Перейти к основанию х;
Упростить уравнение, пользуясь свойством логарифма произведения;
Произвести замену переменной;
Решить полученное уравнение;
После обратной замены переменной, исследовать полученные решения по ОДЗ уравнения.