Конспект урока по математике на тему "Показательные уравнения"

Тема урока: Показательные уравнения

Цели урока:

Ход урока

1.Является ли функция               убывающей?

2.Является ли функция                       возрастающей?

3.Является ли показательным уравнение:

4.Объяснение нового материала

Решая уравнения в последнем задании, вы встретились с задачей, которую невозможно решить ни одним из способов, которые мы изучали, поэтому есть необходимость ввести новый метод «Метод замены переменной»

Он заключается в том, что показательную функцию второй степени заменяют новой переменной, получают уравнение, которое решается по дискриминанту. Найденные корни подставляют в заменяемую функцию, но по определению основание а>0 

Решить уравнение :  4х  + 2 х+1 – 24 = 0

Заметим, что 4 х  = (22 ) х = 2 2х = (2 х)2  

                                   2 х+1 = 2?2 х ,

Тогда уравнение примет вид:

(2х)2 + 2?2х – 24 = 0

Введём новую переменную:  у=2х

у2 + 2у – 24 = 0

у1= 4; у2= -6

Возвращаясь к замене, имеем:

2х=4     или     2х = -6

                                   х =2                    не имеет корней

            Ответ: 2.

5.закрепление изученного материала

Решить уравнение, используя метод введения новой переменной

Уровень1

Уровень 2

6.Работа учащихся в парах по сборникам подготовки к экзаменам.

( по вариантам)

1 вариант :     Вариант 9 (2) ,      Вариант 68 (2) ,    Вариант 11 (2)    

• < > актуализация опорных знаний при решении показательных уравнений; обобщение знаний и способов решения; контроль и самоконтроль знаний, умений и навыков; поверка усвоения темы на обязательном уровне, найти новый метод решения показательных уравнений и уравнений, сводящихся к этому виду< > развитие умения применять знания в конкретной ситуации; развитие умения сравнивать, обобщать, правильно формулировать и излагать мысли; развитие навыков реализации теоретических знаний в практической деятельности; развитие интереса к предмету через содержание учебного материала.< > воспитание навыков самоконтроля и взаимоконтроля; воспитание культуры общения, умения работать в коллективе, взаимопомощи; воспитание качеств характера таких как, настойчивость в достижении цели, умение не растеряться в проблемных ситуациях.

  Организационный момент

• Постановка цели урока

• Математический диктант (взаимопроверка)

• Проблемная задача, объяснение нового метода

• Закрепление изученного

• Самостоятельная работа по сборнику для подготовки к экзамену

• Итог, индивидуальное домашнее задание

  1. Организационный момент

     Здравствуйте, садитесь. На протяжении второго курса, мы с вами рассматривали различные виды уравнений. И видели, что они встречаются как в экзаменационных сборниках, так и в задания ЕГЭ , поэтому эпиграф нашего урока будут слова математика  С.Коваля

      « Уравнения – это золотой ключ, открывающий все математические сезамы»

  2. Постановка цели

     Сегодня на уроке мы закрепим знания по теме показательные уравнения, отработаем методы решения уравнений, а так же познакомимся с новым методом.

     Какое уравнение называется показательным?

     Каким свойством обладает функция, если а>0 и а<0?

     Какие методы решения показательных уравнений вы знаете?

  3. Математический диктант

     На листочках при ответе на любой вопрос будете ставить «+»  -  если «да»,  «-»  -  если «нет». Других вариантов ответов нет.  

      

  1. Верно ли, что D показательной функции является R?

  2. Верно ли что, если b>0, то уравнение       имеет один корень?

  3. Верно ли что, если b=0, то уравнение        не имеет корней?

  4. Верно ли, что график показательной функции проходит через точку с координатами (0;1)

  5. Верно ли что, если b<0, то уравнение     имеет корни?

     Выполнить задания со слайдов 4-9. Взаимопроверка, используя критерий выставить оценку. Один обучающийся выполняет задания на интерактивной доске

  1. < >

     №

                                        Способы решения

     №  уравнения

     1

     Приведение обоих частей уравнения к степени с    одинаковым показателем

      

     2

     Вынесение за скобки степени с наименьшим показателем

      

     3

     Деление обеих частей уравнения на выражение, стоящее правой части

      

     4

     Ведение новой переменной

      

     5

     Построение графиков (графический способ)

      

     6

     Исследование свойств монотонной функции

      

     Задание В5 в ЕГЭ проверяет умение решать простейшие уравнения. Данная разработка посвящена одному из разделов задания В5 – это решение показательных уравнений.

      Основной задачей является:

     - проверка качества знаний и умений учащихся;

     -повышение вычислительной культуры учащихся

      

     Представленная проверочная работа состоит из 5вариантов, в каждом из которых по 12 заданий. Задания  данной работы соответствуют прототипам заданий В5 из открытого банка заданий ЕГЭ по математике. Данный материал  можно использовать при подготовке к ЕГЭ. Для удобства проверки приведены ответы.

      

     Показательные уравнения, задания  В5 из открытого банка заданий ЕГЭ вариант1

     1. Найдите корень уравнения .

     2. Найдите корень уравнения .

     3. Найдите корень уравнения .

     4. Найдите корень уравнения: 

     5. Найдите корень уравнения .

     6. Найдите корень уравнения .

     7. Найдите корень уравнения: 

     8. Найдите корень уравнения: 

     9. Найдите решение уравнения: 

     10. Решите уравнение .

     11. Решите уравнение .

     12. Решите уравнение 

      

     Показательные уравнения, задания  В5 из открытого банка заданий ЕГЭ вариант2.

     1. Найдите корень уравнения .

     2. Найдите корень уравнения .

     3. Найдите корень уравнения .

     4. Найдите корень уравнения: 

     5. Найдите корень уравнения .

     6. Найдите корень уравнения .

     7. Найдите корень уравнения: 

     8. Найдите корень уравнения: 

     9. Найдите решение уравнения: 

     10. Решите уравнение .

     11. Решите уравнение .

     12. Решите уравнение .

     Показательные уравнения, задания  В5 из открытого банка заданий ЕГЭ вариант3.

     1. Найдите корень уравнения .

     2. Найдите корень уравнения .

     3. Найдите корень уравнения .

     4. Найдите корень уравнения: 

     5. Найдите корень уравнения .

     6. Найдите корень уравнения .

     7. Найдите корень уравнения: 

     8. Найдите корень уравнения: 

     9. Найдите решение уравнения: 

     10. Решите уравнение 

     11. Решите уравнение .

     12. Решите уравнение 

     Показательные уравнения, задания  В5 из открытого банка заданий ЕГЭ вариант4.

     1. Найдите корень уравнения .

     2. Найдите корень уравнения .

     3. Найдите корень уравнения .

     4. Найдите корень уравнения: 

     5. Найдите корень уравнения .

     6. Найдите корень уравнения .

     7. Найдите корень уравнения: 

     8. Найдите корень уравнения: 

     9. Найдите решение уравнения: 

     10. Решите уравнение .

     11. Решите уравнение .

     12. Решите уравнение .

     Показательные уравнения, задания  В5 из открытого банка заданий ЕГЭ вариант5.

     1. Найдите корень уравнения .

     2. Найдите корень уравнения .

     3. Найдите корень уравнения .

     4. Найдите корень уравнения: 

     5. Найдите корень уравнения .

     6. Найдите корень уравнения .

     7. Найдите корень уравнения: 

     8. Найдите корень уравнения: 

     9. Найдите решение уравнения: 

     10. Решите уравнение .

     11. Решите уравнение .

     12. Решите уравнение 

     Ответы к проверочной работе

      

     1

     2

     3

     4

     5

     6

     7

     8

     9

     10

     11

     12

     1 вариант

     -1

     4

     11

     5

     4,5

     -7,5

     0

     -5

     0,5

     1,5

     1,4

     -2

     2 вариант

     -1

     2

     4

     0

     2,75

     6,5

     12

     2

     0,5

     3

     0,6

     -1

     3 вариант

     -3

     3

     13

     1

     3,75

     0,5

     -2

     -6

     0,5

     -2,5

     2

     2

     4 вариант

     -1

     16

     7

     7

     2,75

     2,5

     4

     -2

     0,5

     1

     0,375

     0

     5 вариант

     -2

     4

     2

     -2

     9,5

     2,5

     -3

     -7

     -2

     -1

     1

     0,5

     Домашнее задание:
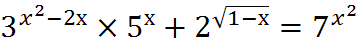
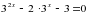
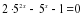
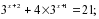
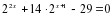
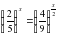
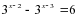
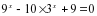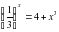
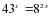
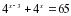
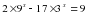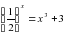