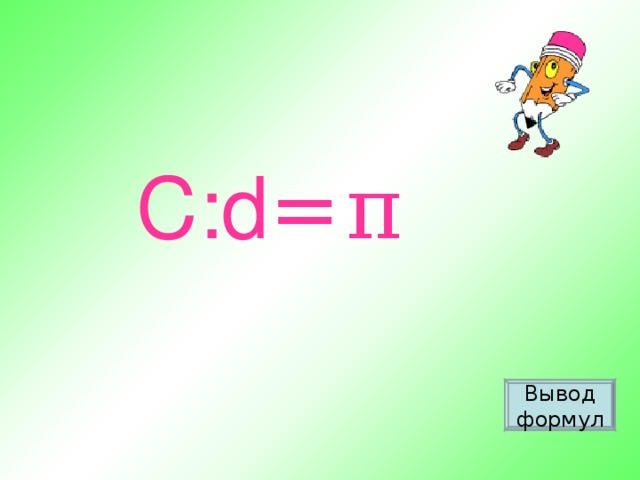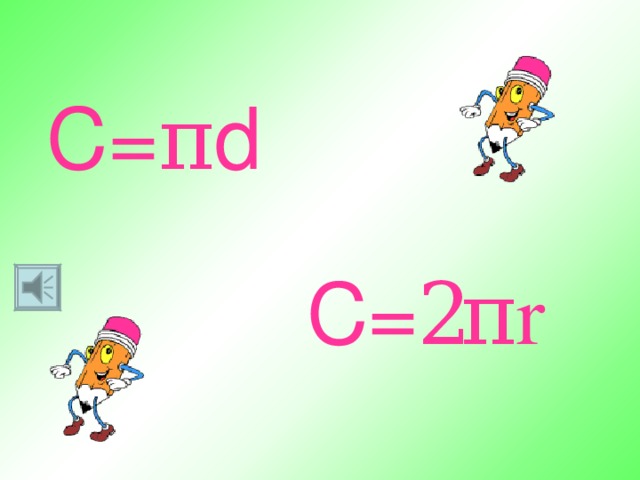«Ұзынкөл ауданының білім беру бөлімі» мемлекеттік мекемесінің «Суворов орта мектебі» коммуналдық мемлекеттік мекемесі Коммунальное государственное учреждение «Суворовская средняя школа» государственного учреждения «Отдел образования Узункольского района»
Урок математики в 6 классе по теме:


Математика мұғалімі: Керейбаева Ғ.С. Учитель математики:Кирибаева Г.С.
Урок математики в 6 классе по теме: «Длина окружности» Тип урока: изучение нового материала. Вид урока: интегрированный. Технология: развивающего обучения, индивидуализации. Время проведения: первый урок по теме: «Длина окружности. Площадь круга. Шар». Цель: изучить формулы длины окружности и показать их применение при решении задач Задачи урока: образовательные: ●изучить формулы длины окружности; ● показать их применение при решении задач; ●познакомиться с числом π; ●прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности. Развивающие: ●развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом; ●развивать навыки устного счёта; ●развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы; ●формировать умения чётко и ясно излагать свои мысли; ●развивать пространственное воображение учащихся. Воспитательные: ●прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности; ●воспитывать умение работать с имеющейся информацией в необычной ситуации; ●воспитывать уважение к математике, умение видеть математические задачи в окружающем нас мире; ●развивать интерес к математике путём создания ситуации успеха. Оборудование и наглядность: • компьютер, интерактивная доска; • презентация слайд-фильм Power Point (приложение 1), флипчарты (приложение 2); • модели окружности, нитка, линейка, калькулятор на каждую парту.
План урока. 1. Активизация внимания. 2.Формулировка темы и целей урока. 3. Актуализация опорных знаний. 4. Изучение новой темы: ●создание проблемной ситуации; ●практическая работа; ●проверка работы; ●вывод; ●историческая справка; ●вывод формул. 5. Физминутка. 6. Первичное закрепление: ●решение задач у доски; ●дифференцированная самостоятельная работа. 7. Тест первичного закрепления. 8. Самооценивание. 9. Домашнее задание. 10. Рефлексия. Ход урока. 1. Активизация внимания (слайд 1).

2. Формулировка темы и целей урока. Учитель: Название нашей темы урока состоит из двух слов. Отгадайте загадку и вы узнаете одно слово темы (презентация слайд 2) Если видишь солнце в небе, или чашку с молоком. Видишь бублик или обруч, слышишь сказку с колобком. В круглом зеркале увидел ты сейчас свою наружность. И вдруг понял, что фигура называется … (окружность) (на экране появляется слово окружности) 
- А другое слово вы узнаете, выполнив следующее задание (презентация слайд 3)
Округлите число до заданного разряда, из предложенных вариантов выберите правильный ответ, каждому числу поставлена в соответствие буква, из букв вы должны составить слово (на экране появляются правильные ответы.)

Так какая тема сегодняшнего урока? (дети отвечают)
Правильно, «Длина окружности» (презентация слайд 4).

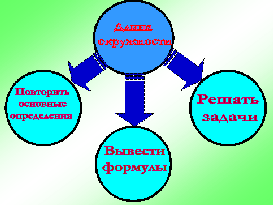
Откройте тетради, запищите число и тему урока: «Длина окружности». Сегодня мы должны (цели урока): 1. Повторить основные понятия темы «Окружность». 2. Вывести формулы для вычисления длины окружности. 3. Учиться применять эти формулы при решении задач (презентация слайд 5).
 3.
3.
3. Актуализация опорных знаний.
1) Что даёт представление об окружности? Приведите примеры (Спортивный обруч, баскетбольное кольцо, кольцо, сделанное из тонкой проволоки и т.д.)
2) С помощью какого инструмента строят окружность? (Транспортир) 3) Давайте вспомним, что мы уже знаем про окружность (презентация слайды 6-9).

-Какая фигура называется окружностью? Как называется точка О?

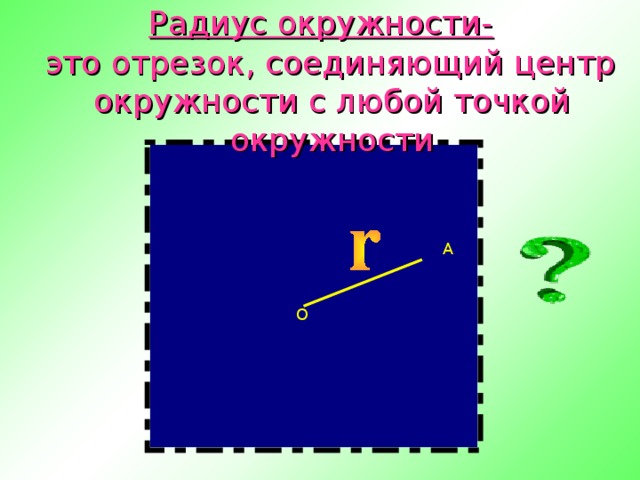
-Что такое радиус окружности? Как обозначается радиус?
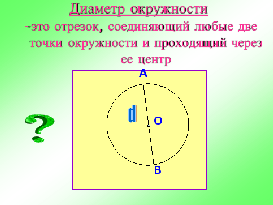
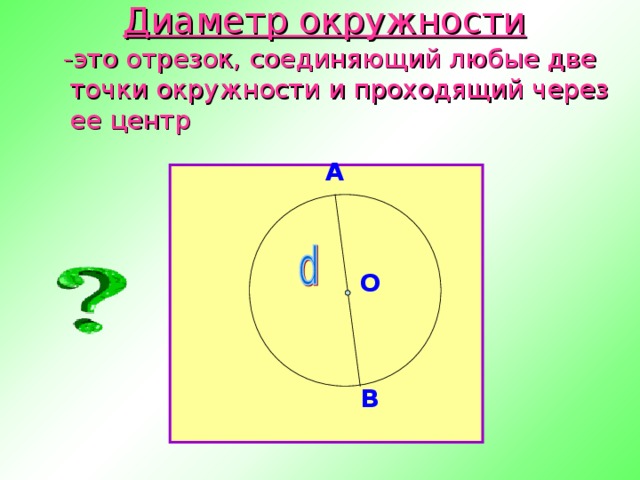
Дайте определение диаметра. Как обозначается диаметр?
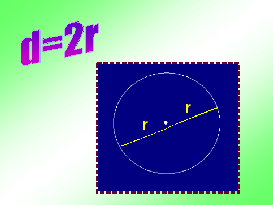
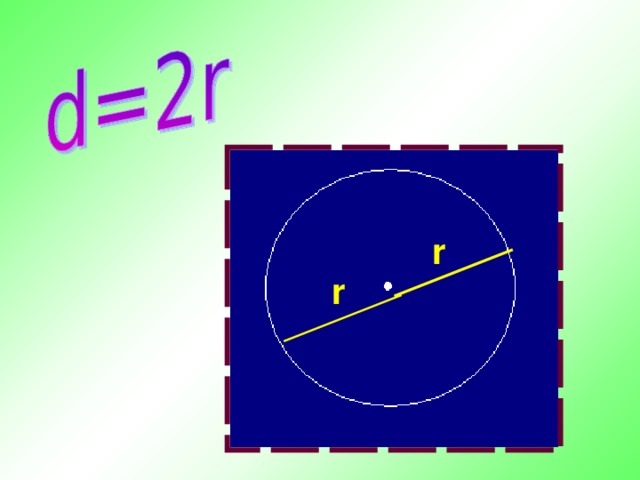
Как связаны радиус и диаметр окружности? (учащиеся отвечают на вопросы учителя)
4. Изучение нового материала: а) Создание проблемной ситуации. (Учитель): - Нам предстоит решить задачу нахождения длины окружности. – Вспомните единицы измерения длины. – С помощью какого инструмента можно измерять длину, например длину отрезка? – А можно ли измерять линейкой длину окружности? – Давайте подумаем, как можно измерить длину окружности? (дети отвечают) (презентация слайды 10-11).

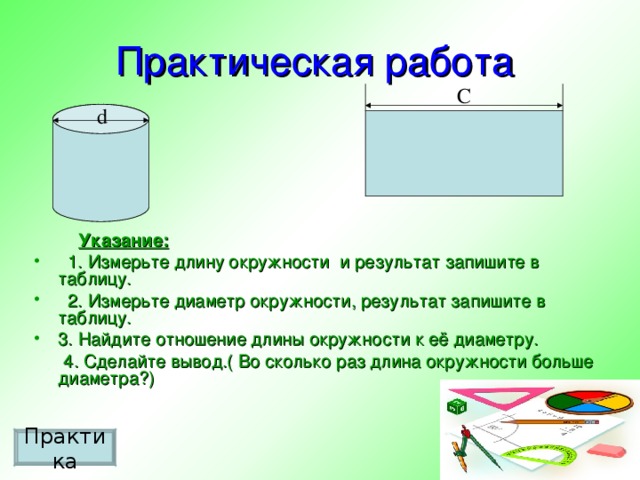
б) Практическая работа (учащиеся выполняют работу) (Учитель): У вас на каждой парте находится модель окружности, линейка, нитка и калькулятор. Эти предметы нам нужны для выполнения практической работы.
Работать вы будете в парах (презентация слайд 12).
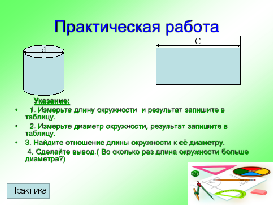
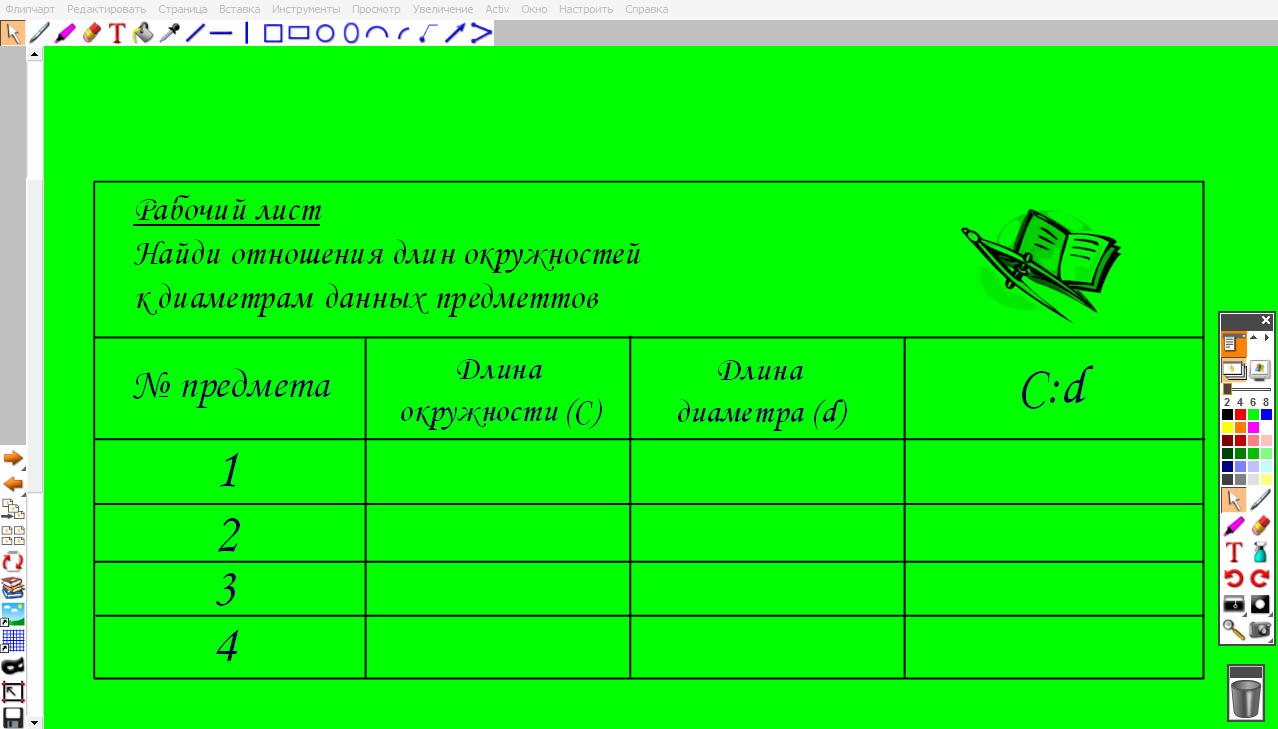
Берёте модель, обвязываете её ниткой, распрямляете и измеряете длину нитки (то есть измеряете длину окружности), затем линейкой измеряете диаметр модели. Найдите отношение длины окружности С к её диаметру d. Результаты измерений внесите в таблицу. Сделайте вывод: во сколько раз длина окружности С больше её диаметра d. (Ребята по одному от каждой пары выходят к доске и записывают под диктовку напарника результаты измерений): С; d; С:d. (флипчарт 1).

в) Проверка работы. У вас были различные модели окружностей, у них разные длины и соответственно разные диаметры. Сравним отношения C:d. (Учитель): - Что у вас получилось? (Результаты примерно одинаковы: C:d
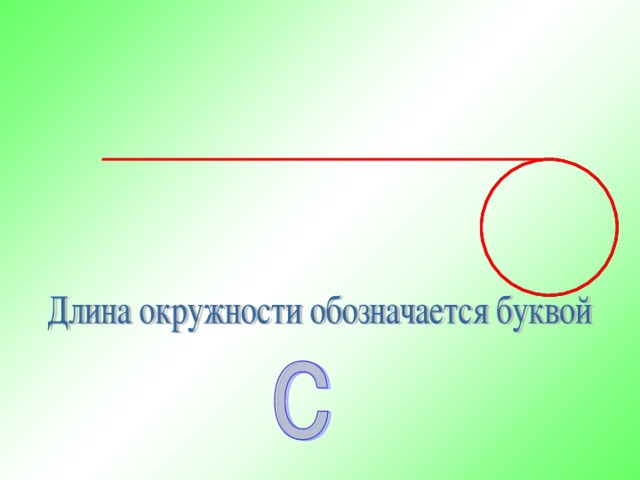
 3,14) г) Формулирование вывода. (Учитель): - Число, которое мы получили, обозначается π. π
3,14) г) Формулирование вывода. (Учитель): - Число, которое мы получили, обозначается π. π
 3,1415926… (презентация слайд 13, флипчарт 2).
3,1415926… (презентация слайд 13, флипчарт 2).

д) Историческая справка (о числе π) (презентация слайды 14, 15)


(Учитель): Число π – бесконечная десятичная дробь. Обозначение числа π происходит от первой буквы греческого слова «периферия», что означает «окружность». Первые 8 цифр числа π можно запомнить так: три, четырнадцать, пятнадцать, девяносто два и шесть (3,1415926).
В практических расчетах редко бывает нужно знать более трех – пяти цифр числа π. Если со временем вы их забудете, то задайте себе вопрос: «Что я знаю о кругах?».
| Что | я | знаю | о | кругах? |
|
|
|
| 3, | 1 | 4 | 1 | 6 |
| Э Т О | Я | З Н А Ю | И | П О М Н Ю | П Р Е К Р А С Н О | П И | Л И Ш Н И Е | З Н А К И | Т У Т
| Ч У Ж Д Ы, | Н А П Р А С Н Ы |
|
|
|
|
3, |
1 |
4 |
1 |
5 |
9 |
2 |
6 |
5 |
3 |
5 |
8 |
Первые 12 цифр можно запомнить с помощью двустишия: Это я знаю и помню прекрасно,
Пи лишние знаки тут чужды, напрасны. В вопросе и двустишии число букв в каждом слове соответствует цифре числа (флипчарт 3)
Сообщения учащихся
1 ученик: На практике часто применяют приближённое значение числа π с точностью до 0,01: π≈3,14. Это приближённое значение числа π впервые использовал великий греческий учёный Архимед (III в. до н.э.). Архимед без измерений, одними рассуждениями вычислил точное значение числа π : π≈
 . Для закрепления в памяти числа Архимеда приведу шутку из учебника Магницкого:
. Для закрепления в памяти числа Архимеда приведу шутку из учебника Магницкого:
Двадцать две совы скучали
На больших сухих суках.
Двадцать две совы мечтали
О семи больших мышах,
О мышах довольно юрких
В аккуратных серых шкурках.
Слюнки капали с усов
У огромных серых сов.
2 ученик:
Обозначение отношения длины окружности к диаметру через число π впервые ввёл Леонард Эйлер (1707 - 1783). Применяя методы высшей математики Эйлер нашёл приближённое значение числа л с точностью до 153-го знака. В наши дни с помощью компьютера можно найти число π с точностью до миллиона знаков после запятой. Однако на практике нет особой необходимости в подобных расчётах.
е) Вывод формул (презентация слайд 16, флипчарт 4 ).
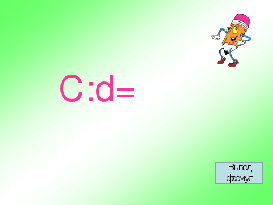
Вернёмся к нашей проблеме нахождения длины окружности. А сможем ли с помощью всё той же нитки найти длину любой окружности? Конечно - же нет, но зная, что С:d=π найдём длину окружности: С=π∙d. Отсюда найдём d. D=С:π. Итак, длина окружности равна произведению её диаметра на число π. Так как d=2r , то С=2πr.
Отсюда найдём r: r=C:2π
- Запишите формулы в тетрадь (презентация слайд 17).

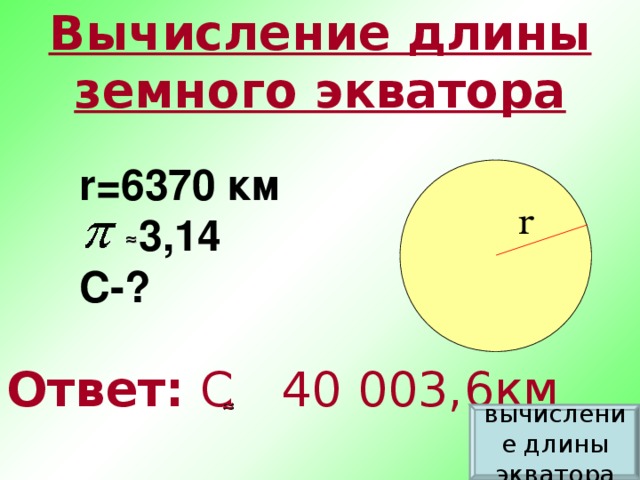
5. Физминутка: А теперь, ребята, встали Быстро руки вверх подняли В стороны, вперёд, назад. Повернулись влево, вправо Тихо сели, вновь за дело. 6. Закрепление изученного. (Учитель): - А что, если мы сегодня на уроке превратимся в ласточек и облетим земной шар по экватору. Давайте вычислим длину экватора. – Форму какой геометрической фигуры имеет экватор Земли? - Что необходимо знать, чтобы найти длину экватора? Задача. R=6370 км. Найти C. Решение: С=2πR С=2∙3,14∙6370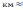
 40003,6 км Ответ:
40003,6 км Ответ: 
 40003,6 км (презентация слайды 18, 19, флипчарт 5).
40003,6 км (презентация слайды 18, 19, флипчарт 5).


(Учитель) : - А сейчас я приглашаю вас в цирк. Как вы думаете, почему в цирк? Какая связь с нашей темой урока? (презентация слайды 20,21).
 -
-
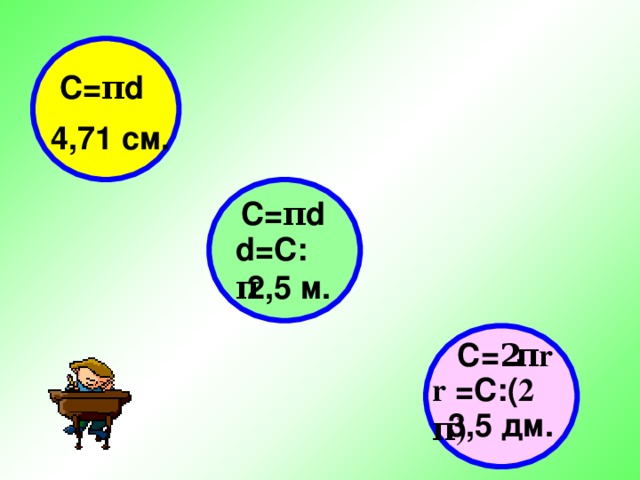
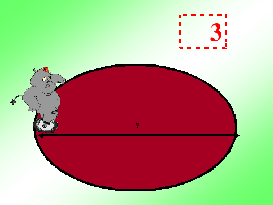
Внимание, аттракцион «Бегемот Пумпа на велосипеде». – Пумпа совершает один круг по арене за 3 минуты, если едет со скоростью 13,5 м/мин. Каков диаметр арены? (Учитель): - Мы решили несколько задач и вы можете уже сказать насколько хорошо или не очень вы усвоили формулы. На презентации (слайд) 3 задачи разного уровня: первая – самая простая, вторая – посложнее, а третья – ещё сложнее. – Прочтите задачи и выберите одну для самостоятельного решения (презентация слайды 22,23, флипчарт 6).

Кто выбрал задачу 1? Задачу 2? Задачу3? От каждой группы по одному представителю у доски (каждый из них решает на доске выбранную задачу). Давайте сверим ответы.
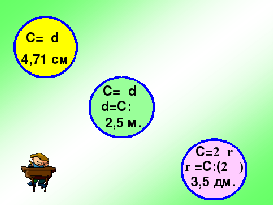 - Поднимите руку, кто верно выполнил задание.
- Поднимите руку, кто верно выполнил задание.
7. Тест первичного закрепления (презентация слайд 24, флипчарт 7)


8. Самооценивание. (Учитель): - Кто справился с тестом на отлично? Поставьте оценки в дневники (презентация слайд 25)

9. Домашнее задание. Поскольку математика тесно связана с жизнью, с окружающей нас средой, в чём вы сегодня убедились, то и задание будет творческое. Может, вы увидите окружность в колесе, может в цирке, а у кого-то есть велосипед, у мамы на кухне кастрюли, кто-то крутит обруч, а кто-то любит искать города на глобусе. Придумайте и составьте задачу по теме «Длина окружности» и сделайте к задаче красочный рисунок (презентация слайд 27
 10.Рефлексия. А сейчас давайте вспомним, что сегодня на уроке мы повторили… узнали… закрепили… (презентация слайд 27).
10.Рефлексия. А сейчас давайте вспомним, что сегодня на уроке мы повторили… узнали… закрепили… (презентация слайд 27).
- Что понравилось на уроке? - Что удалось? – Понадобятся ли знания по данной теме в жизни? – Наш урок закончен. Спасибо за урок (презентация слайд 28).














 3.
3. 












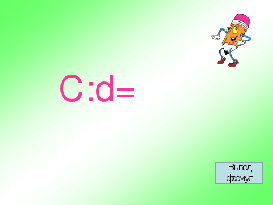



 -
- 
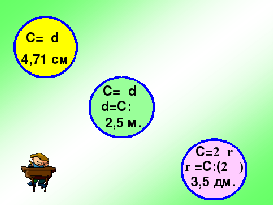 - Поднимите руку, кто верно выполнил задание.
- Поднимите руку, кто верно выполнил задание. 


 10.Рефлексия. А сейчас давайте вспомним, что сегодня на уроке мы повторили… узнали… закрепили… (презентация слайд 27).
10.Рефлексия. А сейчас давайте вспомним, что сегодня на уроке мы повторили… узнали… закрепили… (презентация слайд 27).