Цель создания и использования медиапродукта на учебном занятии - экономия времени, возможность быстро сменить задания, своевременная демонстрация правильного решения, организация повторения и контроля знаний обучающихся в увлекательной игровой форме. Игровая форма организации урока соответствует целям, содержанию, возрастным особенностям учащихся и обеспечивает включение каждого обучаемого в активную учебно-познавательную деятельность. Использование информационных технологий позволяет облегчить учащимся восприятие материала, обеспечить дифференциацию, повысить плотность урока, эффективность контроля знаний и умений учащихся и познавательную активность школьников.
Новизна данного продукта в том, что задания, предложенные на уроке, подбирались с учетом возрастных и индивидуальных особенностей учащихся именно нашей школы и способствовали развитию логического мышления, умения анализировать, применять знания в новых условиях. Задания дифференцированы по уровню сложности. Право выбора соответствующего уровня, предоставляемое ученикам, создало благоприятный психологический климат. Чувство удовлетворения от каждого верно решенного задания, осознание своей успешности в преодолении трудностей дало мощный импульс повышению познавательной активности. Все обучающиеся 8, 9 классов, которые были на уроках с использованием данного продукта, проявили повышенный интерес к урокам математики. Даже ученик, равнодушно и пассивно работающий на обычном уроке, вдруг преобразился, стал инициативным и успешным. Возникновение ситуации успешности стало толчком для развития умения учеников анализировать и оценивать свои знания и знания одноклассников.
Я стала замечать удивление и особый интерес учащихся при решении задач. Кроме этого обучающиеся проявили желание совместно со мной подготовить серию таких презентаций на каждый урок.
По итогам проведения пробных муниципальных тестирований обучающихся 9 классов школы села Верхнее Стярле было отмечено повышение качества знаний на 40%, успеваемости с 40 до 100%.
Данная работа использовалась на уроках математики в 8, 9 классах на уровне школы, во время проведения открытых уроков на районном уровне и на консультациях для обучающихся 9 классов.
Для разработки мультимедийного продукта (медиапродукта) использовалась программа MS PowerPoint 2010.
- Приложение.
Список использованных задач:
- Спрос на товар увеличился в 5 раз. На сколько процентов увеличился спрос? [1; 181]
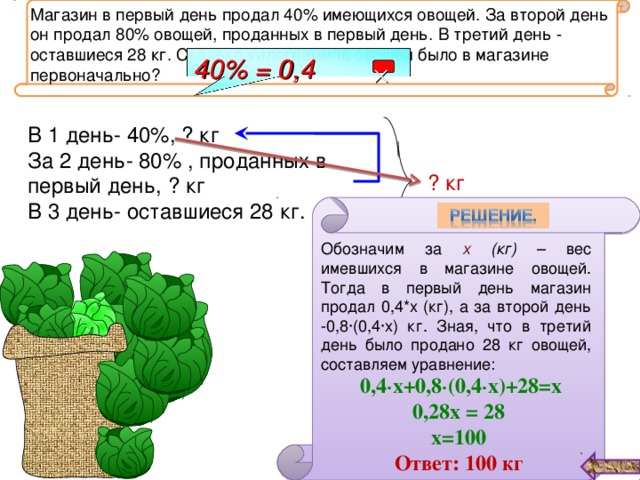
- Магазин в первый день продал 40% имеющихся овощей. За второй день он продал 80% овощей, проданных в первый день. В третий день - оставшиеся 28 кг. Сколько килограммов овощей было в магазине первоначально? [1; 182]
- Сколько литров воды надо добавить к 20 л пятипроцентного раствора соли, чтобы получить четырехпроцентный раствор? [1; 185]
- Имеются два куска сплава меди и цинка с процентным содержанием меди 42% и 65% соответственно. В каком отношении нужно взять эти сплавы, чтобы, переплавив, получить сплав, содержащий 50% меди? [1; 186]
- Скорость велосипедиста от поселка до станции была на 1км/ч больше, чем на обратном пути. На обратный путь он затратил на 2 мин больше. Расстояние между пунктами 7 км. Найдите первоначальную скорость велосипедиста. [1; 186]
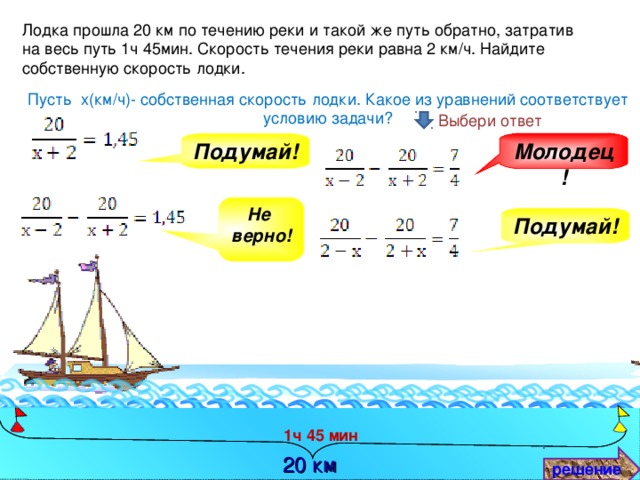
- Лодка прошла 20 км по течению реки и такой же путь обратно, затратив на весь путь 1ч 45мин. Скорость течения реки равна 2 км/ч. Найдите собственную скорость лодки. [1; 187]
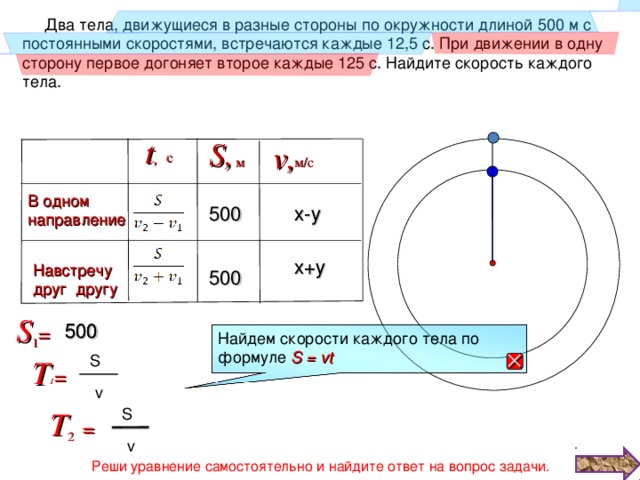
- Два тела, движущиеся в разные стороны по окружности длиной 500 м с постоянными скоростями, встречаются каждые 12,5 с. При движении в одну сторону первое догоняет второе каждые 125 с. Найдите скорость каждого тела. [1; 188]
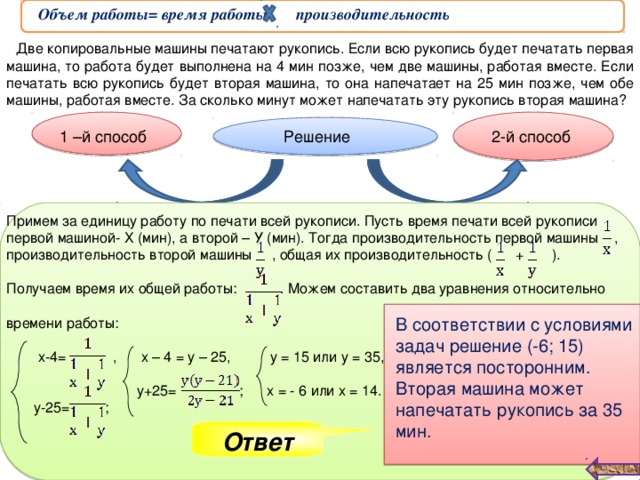
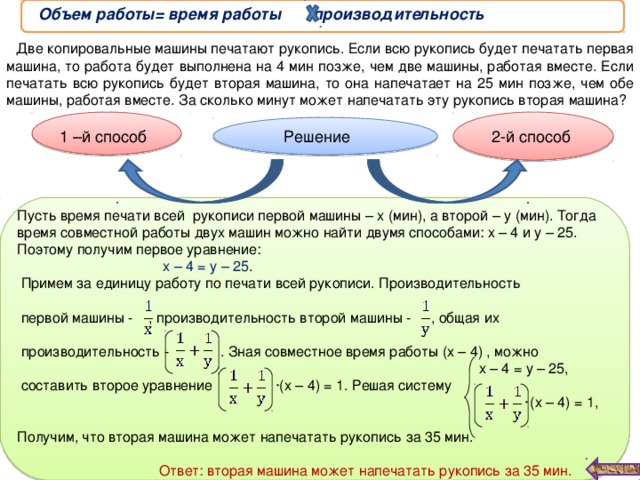
- Две копировальные машины печатают рукопись. Если всю рукопись будет печатать первая машина, то работа будет выполнена на 4 мин позже, чем две машины, работая вместе. Если печатать всю рукопись будет вторая машина, то она напечатает на 25 мин позже, чем обе машины, работая вместе. За сколько минут может напечатать эту рукопись вторая машина? [1; 189]
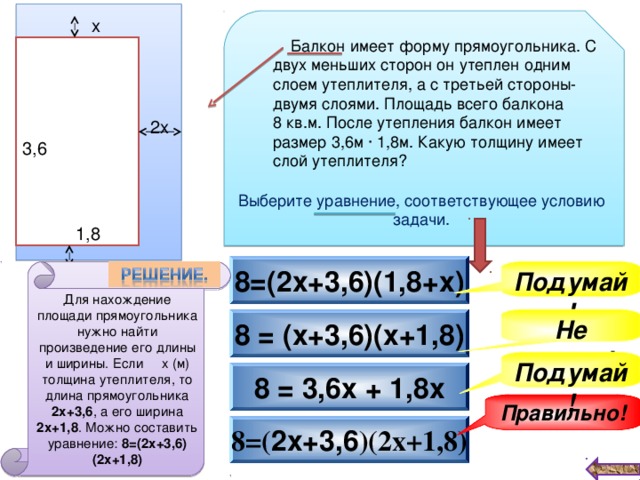
- Балкон имеет форму прямоугольника. С двух меньших сторон он утеплен одним слоем утеплителя, а с третьей стороны - двумя слоями. Площадь всего балкона 8 кв.м. После утепления балкон имеет размер 3,6м ? 1,8м. Какую толщину имеет слой утеплителя? [1; 190]
Литература
1. ГИА 2013. Математика: сборник заданий: 9 класс/ В.В.Кочагин, М.Н.Кочагина. - М.: Эскимо, 2012.-336с.- (государственная (итоговая) аттестация (в новой форме): 9 класс. Сборник заданий)
2. Интернет – источники:
- Карточки по Математике. http://www.razvitierebenka.com/2010/05/blog-post_17.html#.UVbrbRe8B35
- Сайт Савченко Е.М. http://le-savchen.ucoz.ru/
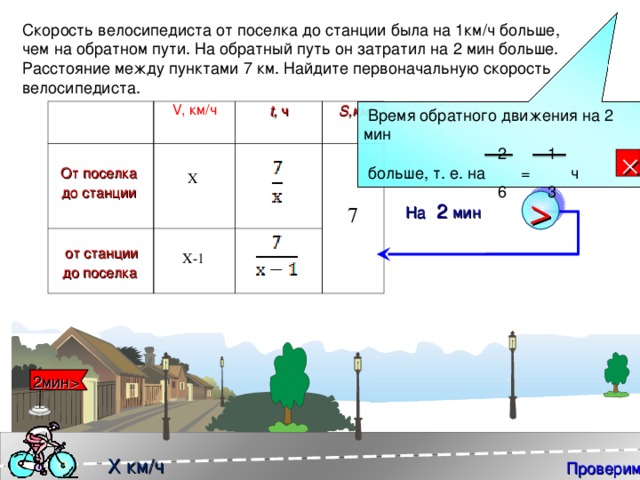Скорость велосипедиста от поселка до станции была на 1км/ч больше, чем на обратном пути. На обратный путь он затратил на 2 мин больше. Расстояние между пунктами 7 км. Найдите первоначальную скорость велосипедиста. Время обратного движения на 2 мин 2 1 больше, т. е. на = ч 6 3 V , км/ч t, ч S, км От поселка до станции Х 7 от станции до поселка Х-1 2мин Х км/ч Проверим" width="640"
