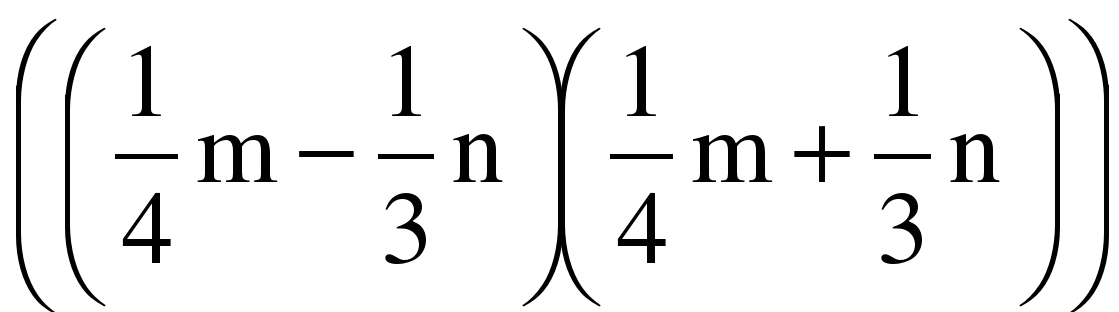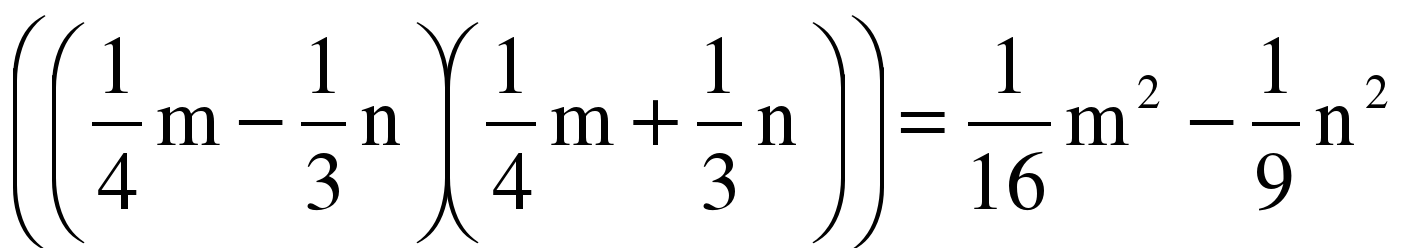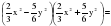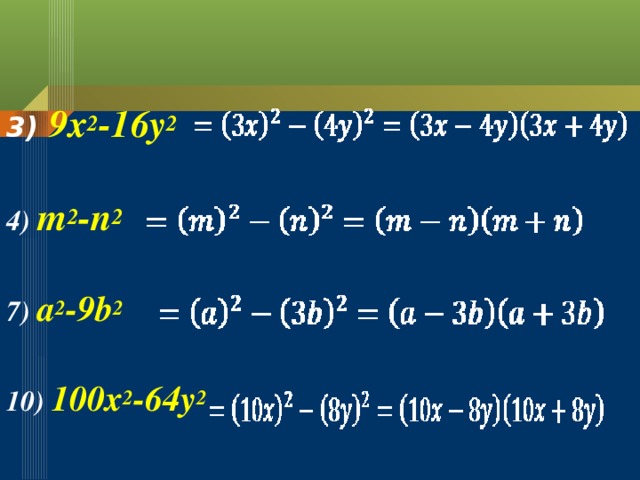Разность квадратов

Цели урока:

Организовать деятельность учащихся на самостоятельный вывод формулы разности квадратов.
Выработать умение распознавать формулу разности квадратов в различных ситуациях, выделять эту формулу из других выражений, применять ее при преобразовании выражений.
Организовать учащихся на доброжелательное отношение друг к другу, на взаимопомощь и взаимовыручку.

Тип урока: урок изучения нового материала

Методы: объяснительно-иллюстративный, частично-поисковый.

Формы урока: индивидуальная, фронтальная, групповая.

Оборудование: компьютер, проектор, презентация, маршрутные листы.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«План урока»

Потехина О.М.

Урок алгебры в 7 классе

Тема: Разность квадратов

Цели урока:

Организовать деятельность учащихся на самостоятельный вывод формулы разности квадратов.
Выработать умение распознавать формулу разности квадратов в различных ситуациях, выделять эту формулу из других выражений, применять ее при преобразовании выражений.
Организовать учащихся на доброжелательное отношение друг к другу, на взаимопомощь и взаимовыручку.

Тип урока: урок изучения нового материала

Методы: объяснительно-иллюстративный, частично-поисковый.

Формы урока: индивидуальная, фронтальная, групповая.

Оборудование: компьютер, проектор, презентация, маршрутные листы.

План урока

1 этап – мотивационно – ориентировочный: разъяснение целей учебной деятельности учащихся и правил.

2 этап – подготовительный : актуализация опорных знаний (в форме «разминки»).

3 этап – основной: постановка проблемы; вывод формулы; проверка формулы; выявление проблемных вопросов; первичное закрепление; запись формулы справа налево; работа с маршрутным листком; проверочная работа.

4 этап – заключительный: подведение общих итогов, домашнее задание.

Ход урокa:

1. Организационный момент. Слайд2
2. Актуализация знаний.
Возведите в квадрат: 3a; 0,2m; (1/3)x; (3/8)y³; 0,03y²		9a²; 0,04m²; (1/9)x²; (9/64)y⁶; 0,0009y⁴ Слайд 3
Представьте в виде квадрата одночлена: 9b²; 16m⁴; 0,09x¹⁰; 0,81m²n²; (16/25)x4y⁶		(3b)²; (4m²)²; (0,3x⁵)²; (0,9mn)²; ((4/5)x²y³)²
На каждом столе лежат маршрутный лист с таблицей, которую нужно заполнить		Работа в парах
На экран проецируются выражения		Слайд 4
a+b 3m-2n 9x²-16 m²-n² 25a²+36b² (3a+2b)² a²-9b²	(m-n)² (4a+3b)² 100x²-64y² (0,2x-0,4y)² 9a+3x²
Заполните таблицу, поместив туда номера соответственных выражений. 1 столбик – квадрат суммы 2 столбик - квадрат разности 3 столбик - разность квадратов 4 столбик - сумма квадратов 5 столбик - остальные выражения		квадрат суммы	квадрат разности	разность квадратов	сумма квадратов	Остальные выражения
		6)	8)	3)	5)	1)
		9)	11)	4)		2)
				7)		12)
				10)
Задание: Сформулируйте формулу квадрата суммы. Раскройте скобки в выражении первого столбца		Решение на доске 6) (3a+2b)²=9a²+12ab+4b² 9) (4a+3b)²=16a²+24ab+9b²
Сформулируйте формулу квадрата разности Раскройте скобки в выражениях второго столбца.		Решение на доске 8) (m-n)²=m²-2mn+n² 11) (0,2x-0,4y)²=0,04x²-0,16xy+0,16y²
Ребята! Еще раз скажите, как называются выражения с номерами третьего столбика? Можете ли вы преобразовать эти выражения?		Разность квадратов Нет
Проблемная ситуация
Тема урока «Разность квадратов»		Пишут в тетради. Слайд 5
Попробуйте сформулировать цели нашего урока		Формулируют, уточняют.
Класс разбивается на три группы. На доске задание.		Представители групп на доске записывают ответы.
Задание: Выполните умножение двучленов		Слайд 6
1 группа (a+b)(a-b) 2 группа (3x-2y)(3x+2y)		1) a²-b² 2) 9x²-4y²
3 группа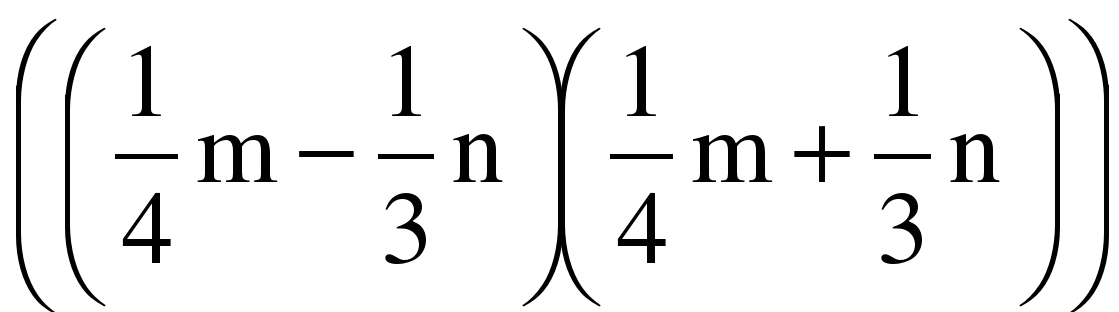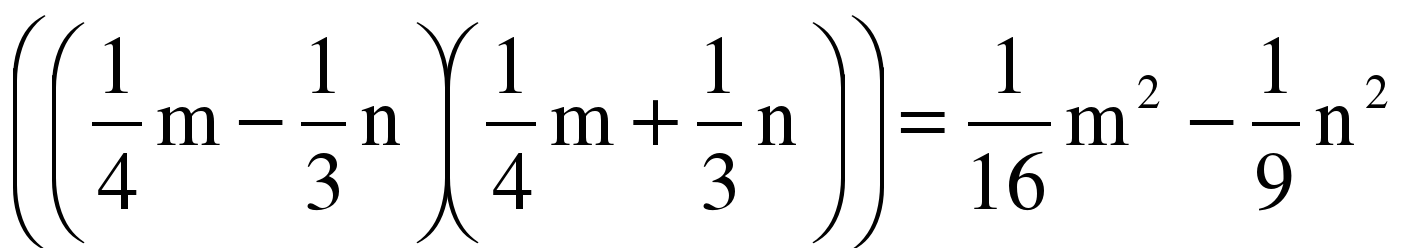
На доске появилась запись (a+b)(a-b)=a²-b² (3x-2y)(3x+2y)=9x²-4y² 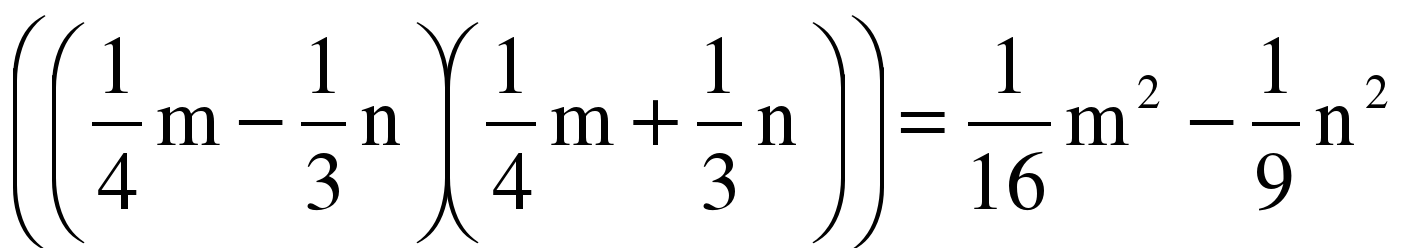Как можно прочитать формулу? (a+b)(a-b)=a²-b²		Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Проверьте справедливость этой формулы при а=5; b=4; а= -2; b=3. Сделайте вывод		а и b - любые числа или выражения
Вопросы , которые позволят нам выявить сущность этой формулы. Слайд 7 Находим ответ на эти вопросы		1) Влияет ли порядок записи скобок на результат? 2) Важен ли порядок записи слагаемых в одной из скобок? 3) Важен ли порядок записи уменьшаемого и вычитаемого в одной из скобок? 4) По какому множителю (а+b) или (а-b) нужно составлять результат?
Выберите выражение, которые могут быть преобразованы по формуле произведения разности выражений на их сумму а) (5+2)(5-2) б) (a-b)-(a+b) в) (x-y)(x+y) г) (0,5-m)(0,5+m) д) ((2/3)-a)((2/3)+a) е) (5x²-3y³)(5x²+3y³)		Слайд 8 а) б) д) е)
Преобразуйте выбранные вами выражения по формуле (a+b)(a-b)=a²-b² Затрудняющимся детям оказываю помощь.		Выполняют самостоятельно. а) (5+2)(5-2)=5²-2²=21 в) (x-y)(x+y)=x²-y² д) ((2/3)-a)((2/3)+a)=4/9-a² е) (5x²-3y³)(5x²+3y³)=25x⁴-9y⁶
Самостоятельная работа 1) Выполнить умножение двучленов, применяя формулу (a+b)(a-b)=a²-b² (5x-3y)(5x+3y)= (0,5m-0,2n)(0,5m+0,2n)= 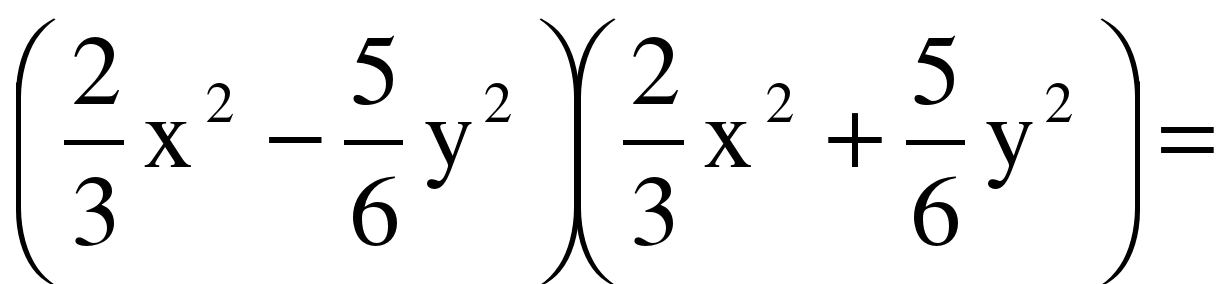(a³-b²)(a³+b²)= (6x⁴-b⁵)(6x⁴+b⁵)=		Слайд 9 Проверяют свою работу по готовым ответам на доске.
Ребята! Давайте посмотрим на формулу (a+b)(a-b)=a²-b²		Слайд 10
Любую формулу в математике можно читать как слева направо, так и справа налево. Всё гармонично в математике. Запишем эту формулу справа налево.		a²-b²=(a+b)(a-b)
Как можно прочитать формулу?		Разность квадратов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на их разность.
Давайте вернемся к нашей таблице и обратим внимание на третий столбец. Используя формулу разности квадратов преобразуйте выражения, номера которых записаны в третьем столбике.		Слайд 11 3) 9x²-16y²=(3x-4y)(3x+4y) 4) m²-n²=(m-n)(m+n) 7) a²-9b²=(a-3b)(a+3b) 10) 100x²-64y²=(10x-8y)(10x+8y)
Замечания. Слайд 12		Не путайте термины « разность квадратов» и « квадрат разности». Разность квадратов– это а² - в², значит , речь идет о формуле (а + в)(а – в) = а² – в²; Квадрат разности – это (а – в)², значит речь идет о формуле а² – 2ав + в²= (а – в )²
Использование формул (фокусы). Слайд 13		71* 69 = (70 – 1)(70 + 1) = 70²- 1² =4900 – 1 = 4899; 82*78 = (80 + 2)(80 – 2) = 80² – 2² = 6400 – 4 = 6396.
Проверочная работа 1. Выполните умножение а) (12-t)(12+t) б) (8а-1)(8а+1) в) (8m-9n)(8m+9n) г) (8d+6c²)(8d-6c²) д) (10m⁸+8n⁸)(10m⁸-8n⁸) 2. Представьте в виде произведения а) с⁴-25 b) 0,16х⁶-9х⁸		Слайд 14. Выполняют работу и проверяют ее друг у друга по готовым ответам, записанным на доске.
Подведение итогов урока 1. С какой новой формулой мы сегодня познакомились? 2. Что нового мы сегодня узнали? 3. С какими трудностями вы сегодня встретились? 4. На что следует обращать внимание при применении формулы (a+b)(a-b)=a²-b²		Слайд 15 С формулой разности квадратов
Домашнее задание		Слайд 16 п. 6.4, № 377 (а-д), № 380 (а-в)
Оценки за урок

Просмотр содержимого документа
«Маршрут урока»

№

содержание

баллы

Устные упражнения

Возведите в квадрат:
3a; 0,2m;
(1/3)x;
(3/8)y³;
0,03y²4 :
0,5

Представьте в виде квадрата одночлена:

9b²
16m⁴
0,09x¹⁰
0,81m²n²

1) a+b
2) 3m-2n
3) 9x²-16
4) m²-n²
5) 25a²+36b²
6)(3a+2b)²
7) a²-9b²

8) (m-n)²
9) (4a+3b)²
100x²-64y²
(0,2x-0,4y)²
9a+3x²

Заполните таблицу:

Выражения
квадрат суммы
квадрат разности
- разность квадратов
сумма квадратов
остальные выражения

Сформулируйте формулу квадрата суммы.

Раскройте скобки в выражении первого столбца

Сформулируйте формулу квадрата разности

Раскройте скобки в выражениях второго столбца.

Выполните умножение двучленов

Произведение разности двух выражений и их суммы равно ------------------------------

Проверьте справедливость этой формулы при а=5; b=4; а= -2; b=3.

Выберите выражение, которые могут быть преобразованы по формуле произведения разности выражений на их сумму

а ) (5+2)(5-2)

б) (a-b) - (a+b)

в) (x-y)(x+y)

г) (0,5-m) + (0,5+m)

д)

е) (5x²-3y³)(5x²+3y³)

Самостоятельная работа

Выполнить умножение двучленов, применяя формулу (a+b)(a-b)=a²-b²

(5x-3y)(5x+3y)=

(0,5m-0,2n)(0,5m+0,2n)=

(a³-b²)(a³+b²)=

(6x⁴-b⁵)(6x⁴+b⁵)=

a²-b²= (a+b)(a-b)

Разность квадратов двух чисел (выражений) равна __________________ суммы этих чисел (выражений) на их разность.

3) 9x²-16y² =

4) m²-n² =

7) a²-9b² =

10) 100x²-64y² =

Проверочная работа

1. Выполните умножение

а) (12-t)(12+t)=

б) (8а-1)(8а+1)=

в) (8m-9n)(8m+9n)=

г) (8d+6c²)(8d-6c²)=

д) (10m⁸+8n⁸)(10m⁸-8n⁸)=

2. Представьте в виде произведения

а) с⁴-25=

b) 0,16х⁶-9х⁸

по 1

ИТОГО:

Оценка

МАРШРУТНЫЙ ЛИСТ

ученика(цы) 7 класса _____________________

тема урока:

Просмотр содержимого документа
«Пояснительная записка»

Потехина Ольга Михайловна МОУ «Ивановская средняя общеобразовательная школа» Курская области

Пояснительная записка

Класс: 7

Дисциплина: алгебра

Раздел: Формулы сокращенного умножения.

Тема: Разность квадратов.

Тип урока: урок изучения нового материала.

Методы: объяснительно-иллюстративный, частично-поисковый.

Формы урока: индивидуальная, фронтальная, групповая.

Оборудование: компьютер, проектор, презентация, маршрутные листы у каждого обучающегося.

Автор: Потехина Ольга Михайловна, учитель математики,

МОУ «Ивановская средняя общеобразовательная школа».

Авторы учебника, учебно-методического комплекса - С.М. Никольский, М.К. Потапов и др. Алгебра: Учебник для 7 класса общеобразовательных учреждений. – М.: Просвещение, 2009.

Необходимое оборудование и материалы для занятия – компьютер, проектор, маршрутные листы.

Описание мультимедийного продукта (медиапродукта):

MS PowerPoint Презентация

Цель создания и использования медиапродукта на занятии - визуализация рабочего пространства, активизация познавательной деятельности.

Как реализуется на уроке (время и место) – на всём протяжении урока.

Презентация к уроку проводится с помощью программы Power Point. Смена слайдов производится по щелчку.

Список использованной литературы:

Алгебра. 7 класс: для общеобразоват. учреждений/С.М. Никольский, М.К. Потапов.- М.:Просвещение, 2009.
Дидактические материаллы по алгебре. 7 класс. А.В. Шевкин, М.К. Потапов.
Маршрутный лист создан на основе

http://festival.1september.ru/articles/511984/

http://images.yandex.ru/yandsearch?ed=1&rpt=simage&text=%D0%BB%D0%B5%D1%80%D0%BC%D0%BE%D0%BD%D1%82%D0%BE%D0%B2&img_url=lingua.russianplanet.ru%2Flibrary%2Flermontov%2Fimages%2Fmlermontov.jpg&p=1&reqtime=1291636463 Фото Лермонтова М.Ю.
http://artmedia.dp.ua/index.php?option=com_content&view=article&id=67%3Ascklipart&catid=22%3A2010-01-26-22-36-02&Itemid=114&showall=1 картинки

Просмотр содержимого презентации
«Разность квадратов»

Разность квадратов

МОУ «Ивановская средняя общеобразовательная школа»

Учитель математики I категории Потехина Ольга Михайловна

"Проверить алгеброй гармонию"

Михаил Юрьевич

Лермонтов

Устные упражнения

Возведите в квадрат:

3a; 0,2m; x; y 3 ; 0,03y 2

Представьте в виде квадрата одночлена:

9b 2 ; 16m 4 ;

0,09x 10 ; 0,81m 2 n 2

Маршрутные листы

a+b
3m-2n
9x 2 -16
m 2 -n 2
25a 2 +36b 2
(3a+2b) 2
a 2 -9b 2
(m-n) 2
(4a+3b) 2
100x 2 -64y 2
(0,2x-0,4y) 2
9a+3x 2

Разность квадратов

Произведение разности двух выражений (чисел) и их суммы равно разности квадратов этих выражений (чисел).

1 ряд (a+b)(a-b)

2 ряд (3x-2y)(3x+2y)

3 ряд

Влияет ли порядок записи скобок на результат? Важен ли порядок записи слагаемых в одной из скобок? Важен ли порядок записи уменьшаемого и вычитаемого в одной из скобок? По какому множителю (а + b) или

Влияет ли порядок записи скобок на результат?
Важен ли порядок записи слагаемых в одной из скобок?
Важен ли порядок записи уменьшаемого и вычитаемого в одной из скобок?
По какому множителю (а + b) или

(а - b) нужно составлять результат?

a) (5+2)(5-2)

б) (a-b)-(a+b)

в) (x-y)(x+y)

г) (0,5-m) +(0,5+m)

д)

е) (5x 2 -3y 3 )(5x 2 +3y 3 )

а) =5 2 -2 2 =21

в) =x 2 -y 2

д )

е) = 25x 4 -9y 6

Самостоятельная работа

(5x-3y)(5x+3y)=

(0,5m-0,2n)(0,5m+0,2n)=

(a 3 -b 2 )(a 3 +b 2 )=

(6x 4 -b 5 )(6x 4 +b 5 )=

(a+b)(a-b) = a 2 -b 2

a 2 -b 2 = (a+b)(a-b)

Разность квадратов двух чисел (выражений) равна произведению суммы этих чисел (выражений) на их разность .

3) 9x 2 -16y 2

4) m 2 -n 2

7) a 2 -9b 2

10) 100x 2 -64y 2

Замечание

Не путайте термины « разность квадратов» и « квадрат разности».

Разность квадратов – это а ² - в² ,

значит , речь идет о формуле

(а + в)(а – в) = а 2 – в 2 ;

Квадрат разности – это (а – в)² ,

значит речь идет о формуле

а 2 – 2ав + в 2 = (а – в ) 2

Формула разности квадратов, используется для математических фокусов. Смотрите:

71∙ 69 = (70 – 1)(70 + 1) = 70 2 - 1 2 =4900 – 1 = 4899;

82∙78 = (80 + 2)(80 – 2) = 80 2 – 2 2 = 6400 – 4 = 6396.

Проверочная работа

1 . Выполните умножение

а ) (12-t)(12+t)=

б) (8а-1)(8а+1)=

в) (8m-9n)(8m+9n)=

г) (8d+6c 2 )(8d-6c 2 )=

д) (10m 8 +8n 8 )(10m 8 -8n 8 )=

2 . Представьте в виде произведения

а) с 4 -25 =

b) 0,16х 6 -9х 8 =

Подведение итогов урока

1. С какой новой формулой мы сегодня познакомились?

2. Что нового мы сегодня узнали?

3. С какими трудностями вы сегодня встретились?

4. На что следует обращать внимание при применении формулы (a+b)(a-b)=a 2 -b 2

Домашнее задание

п. 6.4

№ 377 (а-д)

№ 380 (а-в)

Ваша оценка:

34 баллов и более – «5»
26-33 баллов – «4»
17-25 баллов – «3»
Менее 17 баллов – «2»

Источники

Алгебра. 7 класс: для общеобразоват. учреждений/С.М. Никольский, М.К. Потапов.- М.:Просвещение, 2009.
Дидактические материаллы по алгебре. 7 класс. А.В. Шевкин, М.К. Потапов.
Маршрутный лист создан на основе

http://festival.1september.ru/articles/511984/

http://images.yandex.ru/yandsearch?ed=1&rpt=simage&text=% D0%BB%D0%B5%D1%80%D0%BC%D0%BE%D0%BD%D1%82%D0%BE%D0%B2&img_url=lingua.russianplanet.ru%2Flibrary%2Flermontov%2Fimages%2Fmlermontov.jpg&p=1&reqtime=1291636463 Фото Лермонтова М.Ю.
http:// artmedia.dp.ua/index.php?option=com_content&view=article&id=67%3Ascklipart&catid=22%3A2010-01-26-22-36-02&Itemid=114&showall=1 картинки