"РАВНОВЕЛИКИЕ ФИГУРЫ"
Скажи мне – и я забуду,
Покажи мне – и я запомню,
Вовлеки меня – и я пойму.
Древняя китайская мудрость
Цели урока:
Введение понятия равновеликих фигур, вывод формул площади параллелограмма и треугольника; формирование конструктивного мышления, умений и навыков решения задач на применение введённых понятий и формул площадей;
Формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры; развитие навыков самостоятельной работы.
Воспитание культуры личности, отношения к математике, воспитание ответственного отношения к учебному труду.
Оборудование: Мультимедиа проекто,
ХОД УРОКА
I. Организационный момент
Учитель: Как вы думаете, какова цель сегодняшнего урока? (учащиеся формулируют цель урока).
Ещё можно дополнить сформулированную цель урока следующим: познакомится с понятием равносоставленных фигур, вывести формулы площадей параллелограмма и треугольника.
Сообщение темы и цели урока.
II. Формирование новых понятий и способов действий
1. Введение понятия равносоставленных и равновеликих фигур.
А начнём мы изучать новый материал с решения проблемы.
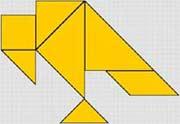
На экране одноцветная фигура «Танграм» [1] («Интерактивная математика 5-9» Площади фигур.)
Вопрос. Как найти площадь данной фигуры, изображающей силуэт птицы?
Возможный вариант ответа: Разрезать данную фигуру на известные геометрические фигуры, найти сумму их площадей.
Учитель. Да, вы правы, необходимо, разрезать эту «птицу» на известные геометрические фигуры, и попытаться найти площадь каждой.
Действия учителя. Учитель разбирает «птицу» на части и меняет их цвет.
Вопрос. Теперь мы видим, что эта фигура являлась «хитроумным узором из семи частей», но возникает опять проблема: как, же нам вычислить площадь каждой части, если нам известна только формула площади квадрата или прямоугольника?
Возможный вариант ответа: Необходимо попытаться собрать эти семь частей в квадрат.
Учитель. Да, действительно, необходимо собрать эти семь фигур в квадрат, называемый в древнем Китае «Доска Мудрости».
Действия учителя. Учитель собирает семь геометрических фигур в квадрат.
Учитель. Мы только, что увидели, что и данная фигура, и квадрат составлены из одних и тех же геометрических фигур.
Такие фигуры называются равносоставленными.
А что вы можете сказать о площадях этих фигур? Да, площади равносоставленных фигур равны, а фигуры, имеющие равные площади называются равновеликими.
Вывод. Из всего вышесказанного можно сформулировать свойство площади: если фигура составлена из нескольких фигур, то её площадь равна сумме площадей этих фигур.
2. Вывод формул площадей параллелограмма и треугольника.
1) Вывод формулы площади параллелограмма.
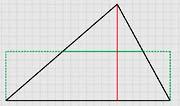
Учитель. Используя, выше сформулированное свойство площади, выведем формулы площадей параллелограмма. Для этого «перекроим» параллелограмм в прямоугольник. Учитель в этой же программе составляет из параллелограмма прямоугольник.
Вопрос. С помощью, какой формулы можно вычислить площадь параллелограмма?
Ответ. S = ah.
Площадь параллелограмма равна произведению высоты и стороны, к которой, проведена эта высота.
Замечание. В случае необходимости, в этом же кадре, начертить параллелограмм и провести его высоту.
2) Вывод формулы площади треугольника.
Работа в парах.
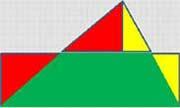
Творческое задание «Голова хорошо, а две – лучше». Разрежьте треугольник на части и составьте из них прямоугольник. Сделайте вывод о формуле площади этого треугольника.
Задание. Объясните способ разрезания треугольника на части.
Варианты ответа. 1. Опустить высоту из вершины треугольника к противолежащей стороне.
2. Провести среднюю линию треугольника, соединяющую середины двух других сторон. Эта средняя линия отсечёт от данного треугольника два треугольника, которые необходимо отрезать и приставить к третьей стороне рассматриваемого треугольника.
Действия учителя. На экране демонстрируется решение данной задачи.
Вывод:
Площадь треугольника равна половине произведения его высоты и стороны, на которую опущена эта высота.
S = ah.
III. Применение знаний, формирование умений и навыков
Замечание. Подготовить диск ОК с программой «Планиметрия 7 – 9».
Закрепим понятие равновеликих фигур и формулы площади треугольника при помощи практической работы.
Практическая работа «Дорогу осилит идущий».
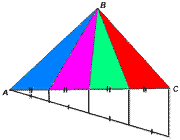
Задание. Разделите треугольник на три (четыре) равновеликих треугольника. Вам понадобятся чертежные инструменты!
1 вариант
На три равновеликих
треугольника.
2 вариант
На четыре равновеликих треугольника.
Инструктаж. При выполнении этой практической работы вам понадобится алгоритм деления данного отрезка на n равных частей. Обратимся к этой задаче помощи специальной компьютерной программы.
Вход в программу (или выйти на нужную тему и задачу через «закладку»).
Учебник. Раздел. ГМТ и геометрические построения.
Тема. Построения циркулем и линейкой.
Задачи. Деление отрезка на n равных частей.
2. Проверка результатов выполнения практической работы.
Учитель. Расскажите, каким образом вы разделили данный треугольник на равновеликие треугольники. Обоснуйте свой ответ.
Решение данной задачи. Необходимо одну из сторон данного треугольника разделить на n равных частей, затем соединить противолежащую вершину с отмеченными точками на стороне.
IV. Первичный контроль за усвоением знаний
Практическая работа «Где руки и охота, там спорая работа».
Задание. Соберите одну фигурку «Танграм».
Дал Бог руки, а веревки сам вей!
Домашнее задание. Найди площадь составленной фигурки «Танграм».
V. Итог урока
Введение понятия равновеликих фигур, вывод формул площади параллелограмма и треугольника; формирование конструктивного мышления, умений и навыков решения задач на применение введённых понятий и формул площадей; 
ah.
