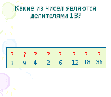
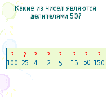
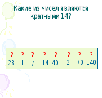
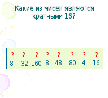
| Создание проблемной ситуации Учитель предлагает выполнить учащимся 3 задания. Учащиеся выполняют задания. Задача 1. Маша испекла 30 кексов. Сколько друзей может пригласить Маша, чтобы каждому досталось одинаковое количество кексов? Задача 2. Лена сплела 71 браслет. Скольким подругам она может подарить браслеты, чтобы всем досталось поровну? Задание 3. Найдите для каждого числа, делители: 50, 7, 829, 31, 24, 10, 21, 5, 100. Обсуждение решений. Решение задачи 1. Надо найти делители числа 30. Д(30) ={1,2,3,5,6,10,15,30} Ответ: Маша может пригласить 1 или 2, или 3 или 5 или 6 или 10 или 15 или 30 друзей. Формативное оценивание «Светофор» (сигнальные карточки ЗЕЛЕНЫЙ – все понятно; ЖЕЛТЫЙ – затрудняюсь; КРАСНЫЙ – не понял) Обратная связь Решение задачи 2. Надо найти делители числа 71. Делители числа 71, которые точно есть это числа 1 и 71. Возникает вопрос: ЕСТЬ ли ЕЩЁ ДЕЛИТЕЛИ у числа 71? Формативное оценивание «Светофор» Обратная связь Решение задания 3. Д(50) ={1,2,5,10,25,50} Д(7) ={1,7} Д(829) = {1, ?,829} Д(31) ={1,31} Д(24) ={1,2,3,4,6,8,12,24} Д(10) ={1,2,5,10} Д(21) ={1,3,7,21} Д(5) ={1,5} Д(100) = {1,2,4,5,10,20, 25, 50, 100} Возникает вопрос про делители числа 829. Есть ли ещё делители, кроме 1 и 829. Сколько их, какие они Формативное оценивание «Светофор» 2. Выход из проблемной ситуации. Устная обратная связь (направление: учитель - ученики) На какие 2 группы можно разделить натуральные числа из задания №3, в зависимости от количества их делителей? Учащиеся предлагают: первая группа чисел, у которых 2 делителя, вторая группа – у которых больше 2-х делителей. 3. Выдвижение гипотез. Диалоговое обучение Вопрос учителя: Как можно назвать каждую группу? Учащиеся выдвигают свои версии. Если версии были, что учитель спрашивает: «А как проверить, правильно ли они назвали каждую группу?», если версий не было, то учитель спрашивает: «Как узнать название каждой группы чисел?». В итоге приходят к мысли, что надо поработать с учебником. 4. Проверка гипотез. Чтение информации на странице 72 - 73 учебника. Учащиеся находят названия обеих групп: простые числа и составные числа и единица дают им определения. Приём «ВЕРНЫЕ - НЕВЕРНЫЕ УТВЕРЖДЕНИЯ» Верно ли, что простое число имеет более двух делителей? Верно ли, что простое число имеет только два делителя? Верно ли, что составное число имеет только один делитель? Верно ли, что составное число имеет более двух делителей? Верно ли, что единица простое число? Верно ли, что единица составное число? Верно ли, что единица ни простое, ни составное число? Формативное оценивание «Светофор»
Дифференцированная индивидуальная работа по карточкам Цель: Знание и понимание Взаимооценивание (проверяют тетради друг у друга) Учитель координирует Критерии оценивания Уровня А: Обучающиеся - Выписывает простые числа - Выписывает составные числа - Записывает произведения в виде составных чисел Уровень А. Выпишите простые и составные числа 10; 7; 12; 8; 11; 24; 49; 30; 34; 2; 68; 53 Запишите числа 18 и 75 в виде произведения составных чисел Критерии оценивания Уровня В: Обучающиеся - Записывает в виде произведения двух простых множителей - Записывает простые числа, удовлетворяющее неравенству - Записывает составные числа, удовлетворяющее неравенству Уровень В. Запишите числа 22; 35; 77; 65; 69; 95 в виде произведения двух простых множителей. Напишите два простых и два составных числа, каждое из которых больше 15 и меньше 25. Критерии оценивания Уровня С: Обучающиеся - Доказывает произведение двух простых чисел, является составным - Показывает примеры произведения простого и составного числа и его результат - Доказывает четность числа Уровень С. Докажите на примерах, что: А) произведение двух простых чисел является составным числом Б) произведение простого и составного чисел является составным числом В) любое четное число, кроме 2, является составным. Формативное оценивание «Светофор». Обратная связь (направление: учитель - ученики) По результатам оценивания по предыдущему заданию дифференцируем группы по уровням А, В, С. (каждый ученик проделывает задания всех уровней, кто выполнит все задания садится в группу С, кто выполнит только задания уровня А, тот садится за группу А) Обучающиеся распределяют роли в группах. Физкультминутка. Давайте лучше узнаем друг друга.
Встаньте те, у кого день рождения выражен простым числом?
А у кого – составным числом?
А у кого – ни простым, ни составным числом? Задание для групп Цель: На применение Приём «РАУНД-ТЭЙБЛ». На ваших столах лежат листочки с заданием. Начинает участник под номером 3. Каждый записывает 1 делитель и передаёт по кругу следующему участнику и так, пока не выполнится всё задание. Я даю вам 1 минуту на выполнение задания. Критерий оценивания для группы А - Использует таблицу простых чисел - Различает простые числа - Различает составные числа - Знает числа – близнецы от 1 до 50 Для группы А. Используя таблицу простых чисел: 66;67;128;139;201;311;450;502;503;641;864;879;991 А) в одну строчку выпишите составные числа в другую простые числа? Б) напишите числа – близнецы от 1 до 50? Критерий оценивания для группы В - Записывает примеры суммы простых чисел - Записывает примеры произведение двух простых чисел Для группы В. Можно ли быть простым числом: А) значение суммы двух простых чисел? Б) значение произведение двух простых чисел? Запишите примеры. Критерий оценивания для группы С - Составляет двухзначные числа из чисел - Различает простые числа - Различает составные числа Для группы С. Запишите все двухзначные числа, которые можно составить из цифр: 1;3;5;7, используя при записи числа каждую цифру только один раз А) какие из них простые числа? Б) какие составные числа? Формативное оценивание «Светофор» Формативное оценивание. Раздел. 5.1В «Делимость натуральных чисел» Цель обучения 5.1.1.6 знать определения простого и составного чисел Уровень мыслительных Знание , понимание и применение навыков Критерий оценивания Обучающийся: - определяет простые и составные числа; - различают простые и составные числа. Задание № 1. Укажите верные высказывания | Простое число имеет только два делителя |
| | Простых чисел бесконечно много |
| | Число 1 является простым |
| | Составное число имеет более двух делителей |
| | Все нечетные числа являются простыми |
| | Все четные числа являются составными |
| | Существуют простые числа, произведение которых является простым числом |
| | Число, следующее за простым числом, составное |
| Дескриптор: Обучающийся - указывает верные высказывания, связанные с определением простых чисел; - указывает верные высказывания, связанные с определением составных чисел.
Задание № 2. Из предложенных чисел 1; 2; 5; 18; 29; 42; 59; 64; 104 выпишите: А) простые числа; Б) составные числа. Дескриптор: Обучающийся - Записывает простые числа; - Записывает составные числа Проверяем задание №№ 1, 2 формативное оценивание (самооценивание)по слайду Устная обратная связь (направление: учитель - ученики) Вопросы: - Какое задание для вас оказалось не понятным? - Какое задание для вас оказалось не сложным? |