Тема урока: Взаимное расположение графиков линейной функции.
Цель:
Задачи:
Ход урока:
I. Организационный момент. Приветствие детей.
II. Актуализация знаний: Что мы изучали на последних уроках?
Что является линейной функцией?
Что является графиком линейной функции?
Математический диктант:
(двое учащихся пишут ответы на закрытой доске, остальные в тетради)
1.Определите значение коэффициентов k и b для каждой из функций
у = 2 – 4х
у = 2х
у = -3
2. Принадлежит ли точка А графику функции у = 3х – 5, если
А(2;1)
3. Решите уравнение:
5х + 2 = 3х
5х + 3 = 7 + 5х
Проверим свои знания .
III. Проверка домашнего задания.
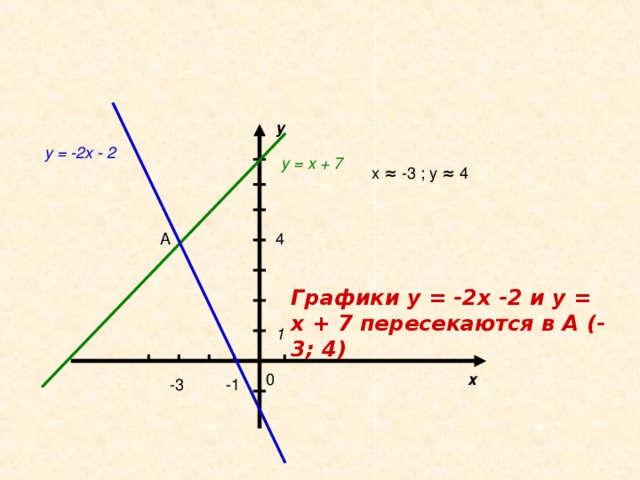
С помощью графиков найти координаты точки пересечения
Ответ:
Графики у = -2х -2 и у = х + 7 пересекаются в А (-3; 4)
IV. Новый материал.
В домашнем задании мы встретились с одним из возможных случаев расположением двух графиков линейных функций. Об этом мы сегодня и поговорим подробнее. Запишем в тетради число, тему урока: «Взаимное расположение графиков линейной функции»
Что является графиком линейной функции?
Каково взаимное расположение двух прямых на плоскости?
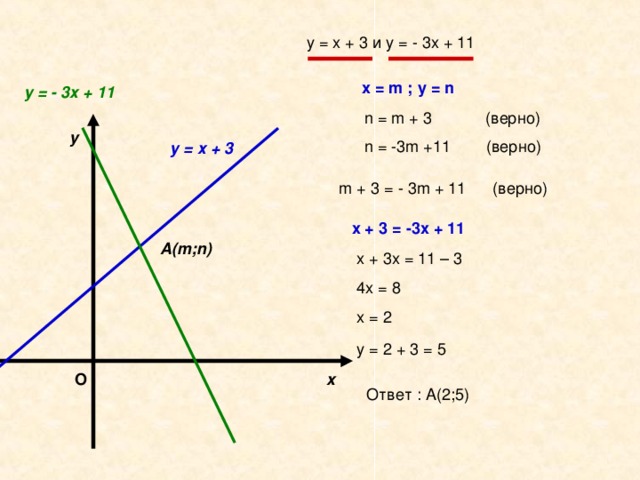
Ребята, посмотрите ,пожалуйста, я построила графики двух линейных функций у = - 3х + 11 и у = х + 3 ,но забыла нанести единичный отрезок. Как мне найти координаты точки пересечения этих графиков?
Что известно про точку А? (Она принадлежит обоим графикам)
Что известно про её координаты? Подставив её координаты вместо х и у мы получаем верные числовые равенства n = m + 3; n = -3m +11.
Посмотрите на левые части этих равенств, какой вывод можете сделать? (Правые части этих равенств равны) m + 3 = - 3m + 11
Вместо чего мы подставляли m? Значит m является корнем какого уравнения? х + 3 = -3х + 11
Решим его х + 3х = 11 – 3
4х = 8
х = 2
Что мы нашли? Как найти ординату точки? (Подставим в любую из формул.)
у = 2 + 3 = 5
Ответ : А(2;5)
Итак, что нужно сделать, чтобы найти координаты точки пересечения графиков линейной функции, не делая построений?
у = k1x + b1 и y = k2x + b2
алгоритм
пример
у = х + 3 и у = - 3х + 11
1. Находим абсциссу точки пересечения графиков.(Составляем уравнение, приравнивая правые части) k1x + b1 = k2x + b2.Решаем уравнение.x = m
1. х + 3 = -3х +11
х + 3х = 11 – 3
4х = 8
х = 2
2. Находим ординату точки пересечения
у = k1m + b1 или y = k2m + b2
2. у = 2 + 3 = 5
у = 5
3. Записываем ответ
(2;5) точка пересечения графиков функций у = х + 3 и у = -3х + 11
У вас на столе есть эта памятка.
V. Найдите координаты точки пересечения графиков у = 3х – 4 и у = 5х + 2. (Один ученик у доски, остальные в тетради.)
VI. Найдите координаты точки пересечения графиков функций у = 2х + 3 и у = 2х + 5(Ребята делают задание в тетради)
1. 2х + 3 = 2х + 5
2х – 2х = 5 - 3
0х = 2
корней нет
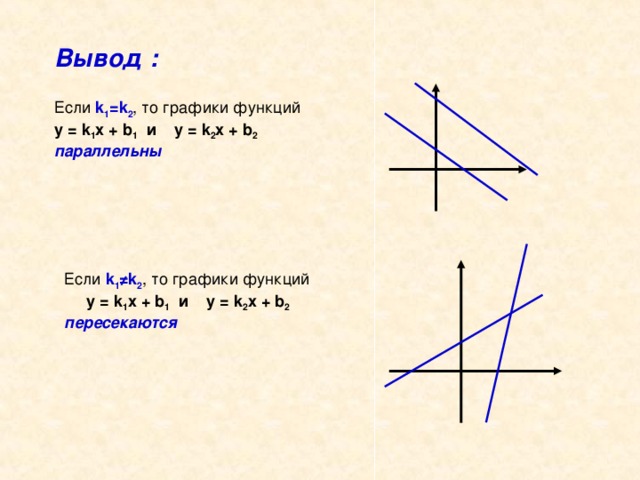
Что получилось? Какой вывод можно сделать?(Значит эти графики не пересекаются)
Посмотрите внимательно на формулы. Почему мы получили 0х = 2?
(Так как коэффициенты при х одинаковы, то при переносе будут противоположны)
Каково взаимное расположение таких прямых?(Они параллельны)
Сделаем вывод. Когда графики функций у = k1x + b1 и y = k2x + b2
будут параллельны?
Когда графики функций у = k1x + b1 и y = k2x + b2
будут пересекаться?
VII. Откроем учебники на стр.62 выполним № 335 устно, давая нужные пояснения.
Выполним № 340 самостоятельно.
у = 10х – 8 и у = -3х + 5
1) 10х – 8 = -3х + 5
10х+3х = 5 + 8
13х = 13
х = 1
2) у = 10·1 – 8
у = 2
Ответ : (1;2) точка пересечения графиков функций у = 10х – 8 и у = -3х + 5
IХ. Домашнее задание.
Откроем дневники запишем домашнее задание п.35,№383,№338.
Х. Подведение итогов.
Что изучили на уроке? Когда графики линейных функций будут параллельны? Когда графики линейных функций будут пересекаться? Как найти координаты точки пересечения ?