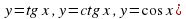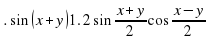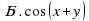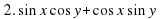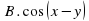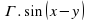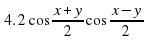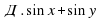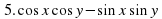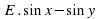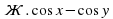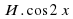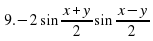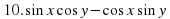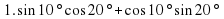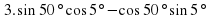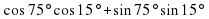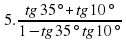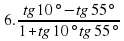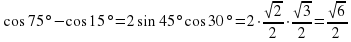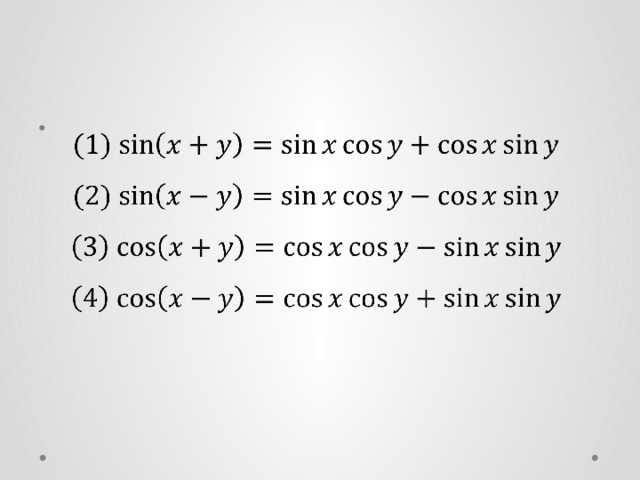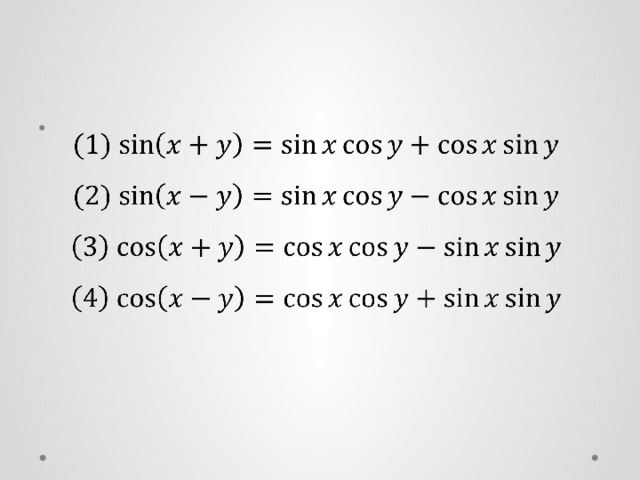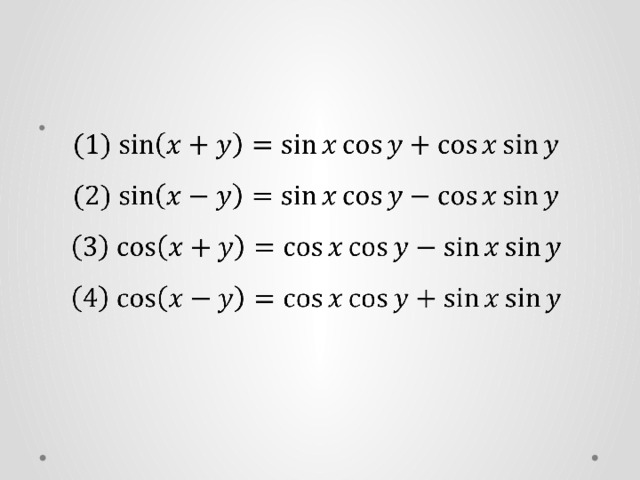Учитель: Кубракова Ирина Анатольевна.
Предмет: Математика.
Класс: 10
УМК:
10 класс. Часть 1. Учебник;
10 класс. Часть 2.Задачник.
Тема урока
"Преобразование произведений тригонометрических функций в суммы».
Тип урока: изучение нового материала.
Цели:
познакомить учащихся с формулами, позволяющими преобразовывать произведение тригонометрических функций в сумму;
формировать умения использовать теоретические знания на практике, развивать умение анализировать, обобщать;
повышать интерес к предмету, к его истории.
Оборудование: Компьютер, презентация, технологическая карта урока.
Ход:
Организационный момент.
Учитель: Сегодня на уроке мы продолжим знакомство с формулами тригонометрии. Эпиграфом к нашему уроку будут слова известного чешского математика, философа Бернарда Больцано: «Формула подчас кажется более мудрой, чем выдумавший ее человек» (Слайды 1-2 ) Как вы думаете о чем идет речь?
Проверка домашнего задания.
Двое учащихся у доски: №28.34(а), №28.17(а)
Актуализация знаний.
3.1. Устная работа. (Слайд 3)
Установи соответствие:
А

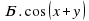
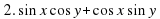
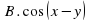
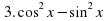
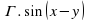
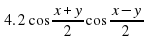
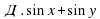
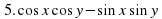

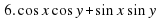
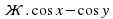

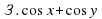

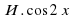
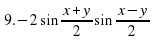
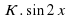
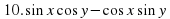
3.2. Математический диктант. (Слайды 4,5)
а) Вычислить:
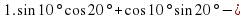 1 вариант.
1 вариант.
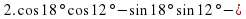 2 вариант.
2 вариант.
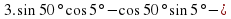 1 вариант.
1 вариант.
4.  2 вариант.
2 вариант.
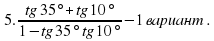
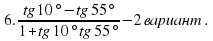
б) Найти ошибку:
1 вариант:
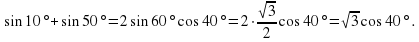
2 вариант:
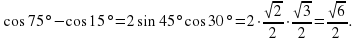
По истечении времени учитель предлагает учащимся поменяться работами друг друга, проверить и оценить их, записав на листах фамилию проверяющего. Правильные ответы демонстрируются на доске. (Слайды 6-8)
3.3. Найти значение выражения. (Слайд 9)
Найти значение выражения:
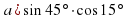 ;
;
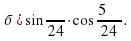
Учащиеся затрудняются найти значения данных выражений. В ходе обсуждения выясняется, что, если бы мы умели произведение двух тригонометрических выражений представлять в виде суммы, то может нам удалось найти значения этих выражений. Учитель предлагает записать тему урока: «Преобразование произведений тригонометрических функций в суммы». (Слайд 10)
Объяснение нового материала.
Учитель: На прошлом уроке мы рассмотрели преобразование суммы и разности тригонометрических функций в произведение. Сегодня мы рассмотрим обратное преобразование, т.е. тригонометрические функции, заданные в виде произведения, преобразуем в сумму или разность. Для вывода этих формул воспользуемся формулами сложения (Слайд 11):
 (1)
(1)
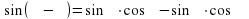 (2)
(2)
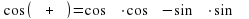 (3)
(3)
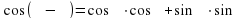 (4)
(4)
Далее учащимся предлагают сложить формулы (1) и (2).
Проверка (Слайд12):
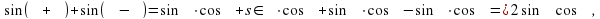
т.е. 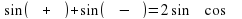 .
.
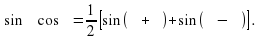
Аналогично, если сложить формулы (3) и (4), получим (Слайд 14):
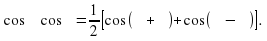
Если рассмотреть разность формул (3) и (4), получим (Слайд16):

Подведем итог. Мы получили три новые формулы, которые позволяют произведение тригонометрических функций представить в виде суммы. (Слайд18)
Теперь мы можем найти значения выражений. (Слайд19) Этим мы займемся после того, как немного отдохнем.
Физкультминутка.
Проверка усвоения нового материала. К доске приглашаются двое учащихся по желанию.
Пример 1. Найдем значение произведения 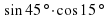 :
:
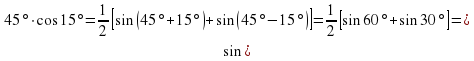
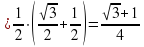 .
.
Пример 2. Вычислим значение выражения 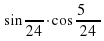 .
.
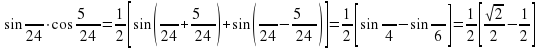
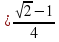 .
.
Учитель: Обсудим еще один существенный вопрос: как при решении конкретного достаточно сложного примера осуществить удачный выбор той или иной формулы. Один рецепт не вызывает сомнений: если можно использовать формулы приведения, то с них и нужно начать. В остальных случаях действуют «три тупых закона»:
Закон №1: “Увидел сумму – делай произведение”;
Закон №2: “Увидел произведение – делай сумму”;
Закон №3: “Увидел квадрат – понижай степень”.
Закрепление. Задачник: №29.4(а); 29.12(б); 29.22(б). Решить на доске и в тетрадях.
Самостоятельная работа:
1 Вариант: №29.2(a)
2 Вариант: №29.2(б).
3 вариант( для сильных учащихся): №29.6(а)
Домашнее задание
§29, №29.1(а,б); 29.4(б); 29.12(а); 29.22(а);
Творческое задание (для желающих): Решить уравнение 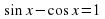 несколькими способами:
несколькими способами:
приведение к однородному уравнению;
разложение на множители;
введение вспомогательного угла;
преобразование разности тригонометрических функций в произведение.
Итог урока
Учитель отмечает хорошую работу одних учащихся, недостаточную активность других. Выставляются оценки.
Рефлексия
Что нового узнали на уроке?
Чему научились?
В чём испытывали трудности?
Оцените свою работу на уроке.
Постройте «график настроения» (один из графиков: 
Собрать работы учащихся.
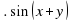

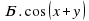
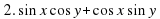
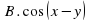
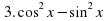
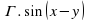
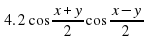
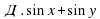
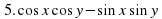

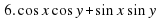
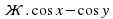

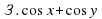

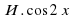
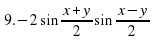
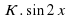
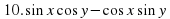
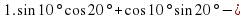 1 вариант.
1 вариант.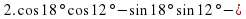 2 вариант.
2 вариант.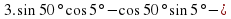 1 вариант.
1 вариант. 2 вариант.
2 вариант.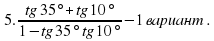
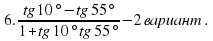
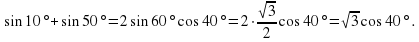
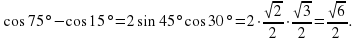
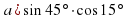 ;
;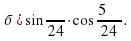
 (1)
(1)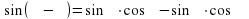 (2)
(2) 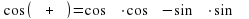 (3)
(3)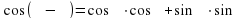 (4)
(4)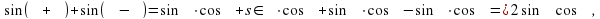
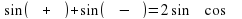 .
.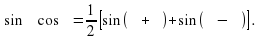
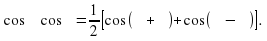

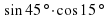 :
: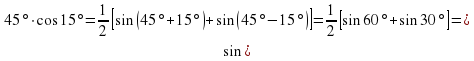
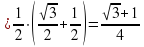 .
.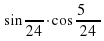 .
.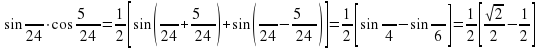
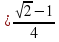 .
.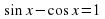 несколькими способами:
несколькими способами: