Методы решения тригонометрических уравнений

Методы решения тригонометрических уравнений

 Учитель математики МБОУ гимназии №30 города Ставрополя

Ивженко Наталья Юрьевна

Метод решения хорош тем, если с самого начала

 мы можем предвидеть – и в последствии

подтвердить это, - что, следуя этому, мы достигнем цели

Лейбниц

Цели урока:

1. Систематизировать, обобщить, расширить знания и умения учащихся, связанные и применением методов решения тригонометрических уравнений.
2. Содействовать развитию математического мышления учащихся, умению наблюдать, сравнивать, обобщать, классифицировать.
3. Побуждать учащихся к преодолению трудностей в процессе умственной деятельности, к самоконтролю, взаимоконтролю, самоанализу своей деятельности.

Оборудование к уроку:

Оценочный лист учащегося, компьютер, проектор, интерактивная доска.

Структура урока:

1. Вводная беседа.
2. Поверка домашнего задания.
3. Работа по теме урока.
4. Подведение итогов.
5. Домашнее задание.

Оценочный лист учащегося

Фамилия _____________________________________________________________________
Имя _________________________________________________________________________

Урок

Этапы

Количество баллов

1

Домашнее задание

I

II

III

2

IV

V

Ход урока

1. Вводная беседа.

Французский писатель Анатоль Франс (1844 – 1924гг) однажды заметил: “Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом.” Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в дальнейшей жизни.

На этом уроке мы поговорим о методах решения тригонометрических уравнений. Мы знаем, что правильно выбранный метод часто позволяет существенно упростить решение, поэтому все изученные методы нужно помнить, чтобы решать конкретные задачи наиболее подходящим методом.

2. Проверка домашнего задания.

На дом было задано простое уравнение, которое надо было решить наибольшим количеством способов.

Ученики отвечают по готовым записям. Работа ведется фронтально, но пары обмениваются тетрадями и проводят взаимопроверку. В ходе проверки проводим сравнительный анализ и комментарий решений.

Предварительное домашнее задание:

Решить уравнение   наибольшим количеством способов. Отмечаем, что в уравнении   a,b,cлюбые действительные числа.

Если , то уравнение теряет смысл, если , то x–любое действительное число.

Способ 1. Сведение к однородному уравнению.

Выразим ,   и 1 через функции половинного аргумента:

;

 |: ;

;

;

;

или

;

, ;

;

, ;

, ;

 

, ;

Ответ: , ; ,.

Способ 2. Введение вспомогательного угла.

A=1,B=1, ; .

;

, ;

, ;

, ;

Ответ: ,.

Способ 3. Преобразование суммы в произведение.

Выразим   через .Получим

;

;

;

;

;

, ;

, ;

, ;

Ответ: ,.

Способ 4. Введение выражений для   и   через   по формулам:

,   (*)

Обращение к функции   предполагает, что , то есть ,.

По формулам (*) исходное уравнение примет вид:

;

;

 |:2

;

;

или

;

, ;

, ;

Ответ:   , ;   ,.

Способ 5. Замена   выражением  .

;

;

;

;

;

;

;

;

или

;

, ;

, ;

Ответ: , ; ,.

Способ 6. Применение формулы  .

;

Исходное уравнение примет вид:

;

;

 , ;

 , ;

Ответ:   ,.

Все решения показываем на тригонометрической окружности точками, отмечаем их совпадения.

Критерии оценок за домашнее задание:

5-6 способов “5” 5б
4 способа “4” 4б
3-2 способа “3” 3-2б
1-0 способов “2” 1-0б

3. Работа по теме урока.

1. Этап I. Тест

Цель: проверить навыки решения простейших тригонометрических уравнений.

Работа проводится по карточкам в двух вариантах, состоящих из 10 уравнений, записанных в столбец. Решая, ученик записывает только ответы, напротив задания, вызвавшего затруднения, ставит прочерк. По истечении времени, отведенного на выполнение теста, листы подписываются и сдаются.

Учитель открывает список ответов и критерии оценок. Проводится быстрая самопроверка. Результаты теста заносятся в оценочный лист. Для оценки работы надо: поставить знак “+” против верного ответа и знак “-” против неверного.

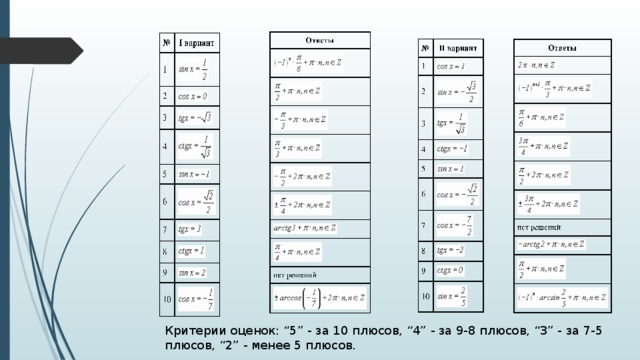
Критерии оценок: “5” - за 10 плюсов, “4” - за 9-8 плюсов, “3” - за 7-5 плюсов, “2” - менее 5 плюсов.

Баллы соответствуют выставленной оценке.

№

I вариант

Ответы

№

II вариант

Ответы

1

1

2

2

3

3

4

4

5

5

6

6

7

7

нет решений

8

8

9

нет решений

9

10

10

Этап II. Классификация тригонометрических уравнений по методам.

Учащимся предлагается провести классификацию уравнений по методам. В таблице напротив каждого уравнения указывается номер метода.

Методы:

1. Разложение на множители.

2. Введение новой переменной:

1. сведение к квадратному;
2. универсальная подстановка;
3. введение вспомогательного аргумента.

3. Сведение к однородному уравнению.

4. Использование свойств функций, входящих в уравнение:

1. обращение к условию равенства тригонометрических функций;
2. использование свойства ограниченности функций.

№

Уравнение

№ метода

1

3

2

1

3

2а,3

4

2а

5

1,2а

6

1

7

2б,2в,3

8

1

9

1

10

4б

11

4а

12

1,2а,2б,2в,4а

13

4а

14

4а

Этап III. После обсуждения вопроса о методах решения уравнений отмечаем, что первые три метода являются традиционными. Последний встречается редко, поэтому остановимся на нем подробнее.

Уравнения, являющиеся равенством двух одноименных тригонометрических функций.

Трое учеников решают на доске № 11, № 13, № 14, остальные учащиеся – любые из этих уравнений.

Уравнение № 11. .

Решение:

Ответ: , ; ,.

Уравнение № 13. .

Решение:

Ответ: , ; ,.

Уравнение № 14. .

Решение: Разделим обе части уравнения на 

;

;

;

Ответ:  ,.

Метод использования свойства ограниченности функции

Если функции f(x) и g(x) таковы, что для всех х выполняются неравенства ,и дано уравнение , то оно равносильно системе уравнений 

Уравнение № 10. 

Решение:

Так как , то , тогда .

Равенство возможно лишь при условии: 

Корни первого уравнения определяются формулой ,. Подставим эти значения x во второе уравнение:   – верно, значит ,  – решение уравнения.

Ответ: ,.

За каждый правильный ответ при обсуждении методов решения уравнений, предложенных в таблице и решении уравнений на этом этапе ученик получает 1 балл.

Этап IV. Рассмотрим три наиболее употребительных приема введения неизвестного при решении тригонометрических уравнений.

1. Замена ,тогда

,

,

Уравнение № 4. 

Решение:

;

;

или

;

;

;

;

нет решений;

,.

 

Ответ: ,.

2. Замена   ,тогда

Уравнение № 5. 

Решение:

Пусть,| t |   1.тогда ,

;

;

;

;

;

или

;

;

нет решений

, ;

 

,.

 

Ответ: ,.

3. Замена , тогда

Уравнение №6. 

Решение:

Заметим, что ,, не являются корнями исходного уравнения. Тогда уравнение примет вид 

или

нет решений

 

, ;

 

,.

 

Ответ: ,.

За верное решение каждого уравнения – 1 балл.

Этап V. Урок завершает самостоятельная работа.

Вариант I - №1, №8.
Вариант II - №2, №9.

Решения собираются. Учащиеся осуществляют самопроверку по готовым решениям. Возникающие при этом вопросы объясняет учитель или ученики, справившиеся с заданием.

Вариант I

Уравнение № 1 

Решение:

 |: 

Пусть , тогда

или

, ;

,

Ответ: , ; ,.

Уравнение № 8. 

Решение: , тогда

Ответ: , ; ,.

Вариант II

Уравнение № 3 

Решение:

 |: 

Пусть , тогда

, 

Ответ: , ; ,.

Уравнение № 9 

Решение: , тогда

Ответ: , ; ,.

Оценка “5” ставится за два правильно решенных уравнений. “4” - за два уравнения, в которых допущена вычислительная ошибка. “3” - за 2 уравнения, в которых допущена грубая ошибка или решено одно уравнение без ошибки, “2” - нет решения или в каждом уравнении допущена грубая ошибка.

4. Подведение итогов.

После проверки самостоятельной работы учитель подводит итог урока: отмечает в какой мере достигнуты цели урока; успехи ребят, обращая внимание к оценочному листу.

Критерии для выставления общей оценки могут быть такими:

18 - 15 баллов – “5”
14 – 12 баллов – “4”
11 – 9 баллов – “3”
менее 9 баллов – “2”

5. Домашнее задание

Учитель дает пояснение к домашнему заданию.

№2, №7, №12 – из таблицы.

№12 – разными способами.

Дополнительно:

1. 

2. 

Литература:

1. Мордкович А. Г. И др. Алгебра и начала анализа. 10 кл.: профильный уровень Задачник для общеобразовательных учреждений. – М.: Мнемозина, 2012.- 340с.: ил.
2. Мордкович А. Г. И др. Алгебра и начала анализа. 10кл.: профильный уровень Учебник для общеобразовательных учреждений. М.: Мнемозина, 2012.- 408с.ил.
3.Мордкович А. Г. Алгебра и начала анализа. 10-11кл.: Методическое пособие для учителя. – М.: Мнемозина, 2010.- 144 с.: ил.
4. Манвелов С. Г. Конструирование современного урока математики. Кн. Для учителя/ С. Г. Манвелов.- М.: Просвещение, 2002.-175с.: ил.
5.Молчалин А.А.Сборник задач по математике с решениями. Учебное пособие. 9-11 классы.- Саратов: “Лицей”, 1998.-128с.
6. Математика. Задачи М. И. Сканави с решениями. Сост. С. М. Марая, П. В. Полуносик.- Мн. изд. В.М. Скакун, 1997.-448 с.
7.Мордкович А. Г. Методические проблемы изучения тригонометрии в общеобразовательной школе. Математика в школе. – 2000.-№ 6 –с.32-38, №6-2002.
8. Звавич Л. И., Пигарев Б. П. Тригонометрические уравнения. Математика в школе.- 1995.- №2 –с. 23-33, №3-с. 18-28.
9. Газизова Р. Решение тригонометрических уравнений. Математика. Еженедельное приложение к газете “Первое сентября”.-2000.-№20.-с.5-9.
10. Шабунин М. И. и др. Алгебра и начала анализа.: Дидактические материалы для 10-11 кл.-М.: Мнемозина, 1997.-253 с.
11. Шарыгин И. Ф. Математика. Для поступающих в вузы: Учебное пособие.- М. : Дрофа, 1997.-416 с.: ил.
12. Домогацких Л. А. Тригонометрия – это просто!/Пособие для учителей, школьников и абитуриентов.- М.: ООО “ТИД “Русское слово – РС”, 2004.-208 с.