Понятие и свойства площади многоугольника

Цели урока: формирования понятия площадь многоугольника; представления об измерении площадей многоугольников; развития способности к обобщению, сравнению; эмоционального восприятия математических объектов.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Понятие и свойства площади многоугольника»

Тема	Понятие и свойства площади многоугольника
Цели урока	формирования понятия площадь многоугольника; представления об измерении площадей многоугольников; развития способности к обобщению, сравнению; эмоционального восприятия математических объектов; формирования представлений о геометрии как способе познания, сохранения и гармоничного развития мира, как части общечеловеческой культуры.
Тип технологии обучения	системно-деятельностный подход
Тип урока	изучение нового материала
Форма урока	урок-исследование, урок творческой деятельности.
Методы обучения	словесные: беседа аудио-визуальные: презентация; логические: индуктивный, дедуктивный;	гностические: продуктивный, творческий; эвристические; проблемно-поисковые.
Формы сотрудничества	индивидуальные; групповые; фронтальные.
Виды учебной деятельности	анализ и решение житейских ситуаций; прогнозирование результата и выполнение вычислений для решения задач; планирование хода решения задач; выдвижение гипотез, доказательства их истинности или ложности; конструирование математических моделей.
Ключевые компетенции	ценностно-смысловая компетенция; общекультурная компетенция; учебно-познавательная компетенция; коммуникативная компетенция; компетенция личного самосовершенствования
Планируемые результаты: личностные	умение понимать смысл поставленной задачи, ясно и чётко излагать свои мысли в устной речи, выстраивать аргументацию, приводить контрпримеры; умение работать в парах и группах. самооценка результатов деятельности, осознание границ применения нового знания; ценностно-эмоциональное отношение к изучаемому математическому содержанию с общекультурных позиций; представление о значении математической науки как сфере человеческой деятельности;
Планируемые результаты: метапредметные	умение выделять главное, сравнивать, обобщать, проводить аналогию, применять индуктивные способы рассуждений, выдвигать гипотезы при решении учебных задач; осознанное чтение текста; способность к интерпретации; представление о геометрии как средстве моделирования явлений окружающего мира; понятия: площади многоугольника, палетка умение вычислять площадь многоугольника по основным формулам, по формуле Пика, а также используя свойства площади; использовать различные языки математики (словесный – символический).

Ход урока

Этапы урока

Деятельность учителя

Деятельность учащихся

Универсальные действия

Самоопределение к деятельности

- Здравствуйте, ребята!

Аристотель говорил: «Ум заключается не только в знании, но и в умении приложить знание на деле». Прокомментируйте – как вы понимаете это высказывание.

Тему сегодняшнего урока вы сформулируете сами.

Для этого устно выполните следующие задания (раздаются карточки). Назовите букву, стоящую в скобках, соответствующую истинному высказыванию (буквы записать на доске).

Из записанных слов составьте слово.

Что вы понимаете под словом «площадь»?

Подготовка класса к работе

Высказывают свои мнения

Площадь

Учащиеся приводят различные примеры

Личностные: самоопределение;

Регулятивные: целеполагание;

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

Актуализация знаний и фиксация затруднений в деятельности

В своей практической деятельности человек часто имеет дело с площадями:

чтобы найти урожайность, надо знать площадь поля; о площади, занимаемой каким-либо государством, вы узнаёте из курса географии;

площадь опоры и площадь поперечного сечения проводника вы должны уметь находить, решая задачи по физике.

Как одним словом назвать фигуры изображённые на экране?

Площади каких фигур вы умеете вычислять?

Чему равна площадь прямоугольника, квадрата?

Умеем ли мы вычислять площадь параллелограмма, ромба, трапеции?

Сформулируйте тему нашего сегодняшнего урока.

Запишите в тетради тему нашего урока.

Сформулируйте цели урока.

Нам предстоит решить несколько проблем по ходу урока. Прежде, чем к этому приступить, давайте определимся с понятием «проблема»? Обратите внимание на слайд и выберите тот вариант трактовки понятия, который вам ближе или составьте своё определение.

Высказывают свои мнения

Многоугольники

Прямоугольника, квадрата

S = аb, S = а²

Нет

Площадь многоугольника

Формулируют цели урока.

Проблема – сложный вопрос, требующий изучения, разрешения.

Аргументированный выбор понятия.

Личностные: Самоопределение ; поиск и выделение необходимой информации; умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.

Создание

проблемной

ситуации

Как найти площадь данной фигуры, изображающей силуэт птицы?

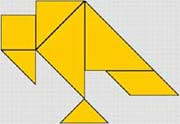
Разрезать данную фигуру на известные геометрические фигуры, найти сумму их площадей

Подбор способа решения проблемы.

Построение проекта выхода из затруднений

Вы правы, эта фигура является «хитроумным узором из семи частей». Площади, каких частей вы можете найти?

С какой трудностью можно столкнуться при выполнении задания? Какую задачу поставим для преодоления этого препятствия?

Наша первоначальная проблема пока не решена, наоборот, возникает следующая проблема: как вычислить площадь каждой части, если нам известна только формула площади квадрата и прямоугольника?

Перед нами две фигуры, составленные из одних и тех же геометрических фигур. Части, на которые разрезана одна фигура, позволили получить другую фигуру. Какую?

Как называются такие фигуры?

Что вам известно о площадях равносоставленных фигур?

Как называются фигуры, имеющие равные площади?

По формулам можно вычислить площади прямоугольника, квадрата.

Необходимо попытаться собрать эти семь частей в многоугольник.

Работа в парах с геометрической головоломкой «Танграм».

Равносоставленные.

Площади равны.

Равновеликие.

Регулятивные: Целеполагание ; выделение и формулирование познавательной цели , анализ ; умение с

достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.

Правильность получения запрограммированного результата.

Открытие

новых знаний.

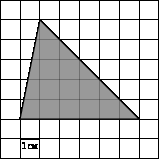
Вспомните, в чём измеряется площадь?

Что означает 1 см²?

При выбранной единице измерение площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и её части укладываются в данном многоугольнике.

Найдите площадь многоугольника АВСD, взяв за единицу измерения закрашенный квадрат.

Вычислять площадь многоугольника таким способом не всегда удобно, поэтому и нужны формулы для вычисления площадей. Вывод этих формул основан на свойствах площадей. Итак, рассмотрим свойства площадей.

Какие фигуры называются равными? (Фигуры называются равными, если при наложении они совмещаются)

Если многоугольники F₁ иF₂ равны, то, что можно сказать об их площадях? (Площади равны) Ответ объясните. (Площади равны, т.к. в равных фигурах единица измерения укладывается одинаковое число раз)

Сформулируйте первое свойство площадей. (Равные многоугольники имеют равные площади)

Если многоугольник разбит на несколько частей, как можно найти его площадь? (Площадь равна сумме площадей его частей)

Сформулируйте второе свойство площадей. (Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников)

Чему равна площадь квадрата со стороной а? (S_кв = а²⁾

Сформулируйте третье свойство. (Площадь квадрата равна квадрату его стороны)

Итак, повторим ещё раз свойства площадей.

мм², см², м², га, а

Площадь квадрата со стороной 1 см

20 кв. ед.

Фигуры называются равными, если при наложении они совмещаются

Равные многоугольники имеют равные площади

Площади равны, т.к. в равных фигурах единица измерения укладывается одинаковое число раз

Площадь равна сумме площадей его частей

Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

S_кв = а²

Площадь квадрата равна квадрату его стороны

Регулятивные: Планирование, контроль, коррекция, оценка, саморегуляция ; моделирование,

самостоятельное создание алгоритмов деятельности, анализ, синтез, построение логической цепи рассуждения, доказательство; Коммуникативные: управление поведением партнёра.

Практическая значимость изученного материала

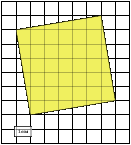
1. Демонстрируется палетка. Что это?

Прибор для вычисления площади фигур – палетка, прозрачная пластинка с нанесенной на неё сеткой линий, предназначенная для вычисления площадей на планах и картах.

Где используется: для решения многих инженерных задач при строительстве новых домов, фабрик, водохранилищ и т.п. требуется знать площади отводимых под строительство земельных угодий. Эти площади могут быть рассчитаны по результатам измерений на местности или определены по карте. Для этого применяют способ разбивки участка на простые геометрические фигуры или используют прозрачную плёнку с нанесёнными квадратами – палетку.

С помощью палетки вам предстоит выполнить задание: найти площадь геометрических фигур.

2. Сто лет назад немецкий математик Георг Пик обнаружил замечательную формулу для вычисления площади многоугольника с вершинами в узлах клетчатой бумаги. Что же это за формула и как она помогает решить проблему вычисления площади, вы узнаете, изучив информацию на стенде или обратившись к одной из поисковых систем сети Интернет, после чего на следующих уроках мы рассмотрим её применение к определенному виду задач

Мозговой штурм.

Учащиеся выдвигают гипотезы по предложенному объекту

Пользуясь палеткой, находят площади фигур. Работа в группах.

Регулятивные: Выбор способа решения задач.

Познавательные: Прогнозирование, коррекция; анализ, аналогия, сравнение, выдвижение гипотез и их обоснование, самостоятельное создание способов решения проблем творческого и поискового характера.

Практическая значимость изученного материала

3. На ваш взгляд, что общего у данных картинок? Почему они появились на одном слайде перед вами?

Это картинки с практической направленностью изучаемого вопроса.

Для чего надо знать площадь поверхности дороги?

Площадь зеркала водохранилища нужно знать проектировщикам для того, чтобы определить, как станет испаряться из заполненного водохранилища вода.

Для чего надо знать площадь поверхности стен в помещении?

Нахождение площади дороги, стены, водохранилища.

При расчете необходимого для её покрытия количества асфальта

Чтобы рассчитать необходимое для покрытия количества краски, обоев или кафеля и т.д.

Коммуникативные: Сотрудничество с учителем и сверстниками, постановка вопросов, умение с достаточной полнотой выражать свои мысли, владение монологической и диалогической формами речи.

П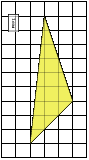рактическая значимость изученного материала

4. Перед вами на слайде расположена схема оригами – древнего японского искусства складывания из бумаги. Первая схема уже выполнена. Вам предлагается сделать остальные пять.

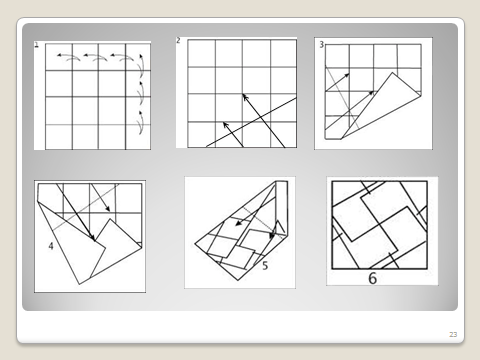
Что в результате получилось? Оцените его площадь, сравните её с площадью первоначального квадрата?

Площадь сделанного вашими руками квадрата в 3 раза меньше площади исходного. Это вы и докажите дома.

А теперь положите ваше произведение искусства на ладонь квадратом вниз и попробуйте ответить на простой вопрос: что это?

Это классический вариант ТАТО. Тато – традиционные японские бумажные плоские коробочки для хранения разных мелочей – булавок, пуговиц, ниток, а в последнее время и

марок. Вот таким образом в Японии решили проблему хранения мелочей. Традиционные тато были шестиугольными или восьмиугольными. Современные мастера часто делают их в форме квадрата, иногда называют конвертами. А как они собираются, открываются, вы узнаете, посетив сайт Страна Мастеров. http://stranamasterov.ru/node/

Практическая работа с цветной бумагой.

Правильность получения запрограммированного результата

Самостоятельная работа с самопроверкой по эталону.

1.Определи, сколько процентов каждой фигуры закрашено

2. Найдите площадь прямоугольника, если его периметр равен 144 см, а стороны относятся как 5:7.

3. Продолжите фразу так, чтобы утверждение стало неверным. «Площадь прямоугольника равна…»

4. Как продолжить утверждение, чтобы оно стало верным:

а) если одну пару противоположных сторон прямоугольника увеличить в 2 раза, то площадь …;

б) если каждую сторону прямоугольника увеличить в 2 раза, то площадь …

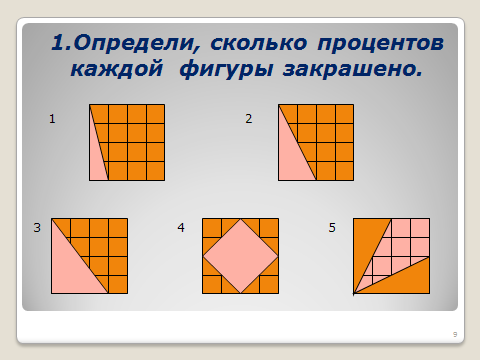
5. АВСD - прямоугольник. Площадь его равна S. Найти площадь треугольника АВМ.

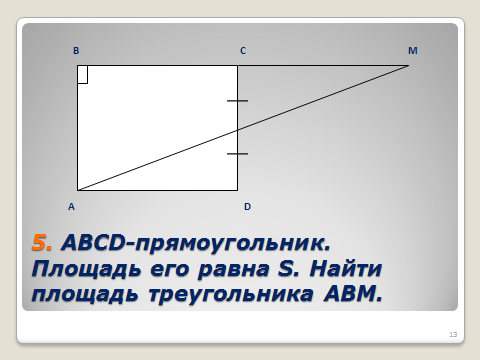
Выполняют самостоятельную работу с самопроверкой по эталону.

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что подлежит усвоению, осознание качества и уровня усвоения;

Познавательные: Активная познавательная мыслительная деятельность.

Выбор наиболее эффективных способов решения задач, самостоятельное создание алгоритмов деятельности, установление причинно – следственных связей;

Коммуникативные: владение монологической и диалогической формами речи.

Рефлексия

Итак, на сегодняшнем уроке мы рассмотрели понятие площади.

- Что нового вы узнали?

- Что повторили?

- Оцените свою работу. Выставите фигурку, которая покажет уровень понимания, того чем мы занимались на сегодняшнем уроке. Начертите отрезок, на одном конце 0 (ничего не понятно) на другом 1 (всё понятно).