Муниципальное казенное общеобразовательное учреждение
"Лозовская средняя общеобразовательная школа Верхнемамонского муниципального района Воронежской области"
Открытый урок на тему:

(Элективный курс "Избранные вопросы математики")
Подготовила и провела
в 11 классе
учитель математики
Волобуева М.В.
2015г.
Цели урока:
Обучающие:
обобщение и систематизация знаний и способов действий;
проверка, оценка и коррекция знаний и способов действий;
обучение самоконтролю, быстрому переключению с одного типа заданий на другой;
повторить основные теоретические сведения по тригонометрии;
повторить формулы тригонометрии, методы преобразования выражений;
рассмотреть примеры заданий С1 ЕГЭ.
Развивающие:
развитие самостоятельности, внимательности;
формирование умения выбирать оптимальную стратегию при решении конкретной задачи и работы в целом;
развитие умения аргументировано участвовать в обсуждении решений;
развитие наглядно-действенного творческого воображения;
Воспитательные:
формирование культуры математической речи;
содействовать воспитанию интереса к математике, активности, мобильности;
воспитание коммуникативной и информативной культуры учащихся.
Тип урока: урок-практикум.
Формы организации урока: индивидуальная, фронтальная.
Методы обучения:
Оборудование:
К уроку подготовлена презентация. С ее помощью проводится устная работа, повторение ранее изученного материала, рассматриваются различные виды тригонометрических уравнений и способы их решения.
Структура урока:
Организационный момент. (1-2 мин.)
Первичное повторение знаний и умений на уровне воспроизведения. (10-12 мин.)
Динамическая пауза. (1-2 мин.)
Систематизация и обобщение знаний и умений при выполнении заданий. (25-30 мин.)
Подведение итогов урока, определения домашнего задания и инструктажа по его выполнению. (3-5 мин.)
Ход урока:
Какое слово начинается с трёх букв «Г» и заканчивается тремя буквами «Я»?
(Тригонометрия)
«Три пути ведут к знанию:
путь размышления – это путь самый благородный,
путь подражания – это путь самый легкий,
и путь опыта – это путь самый горький»
Конфуций
Сегодня от вас потребуется: и умение размышлять (при выполнении каждого задания), и умение подражать (точное знание формул и их применение), и опыт (навык преобразования тригонометрических выражений). И я надеюсь, что все эти пути действительно приведут вас к знаниям, которые позволят вам в будущем успешно сдать ЕГЭ и продолжить свое образование в Вузах.
Тема нашего урока "Решение тригонометрических уравнений".
Сегодня мы повторим формулы, вспомним способы решения тригонометрических уравнений и разберем часть примеров из открытого банка заданий ЕГЭ.
И ещё: именно тригонометрические задания вызывают затруднения при сдаче экзаменов, такой вывод сделала комиссия, которая производила анализ ошибок по ЕГЭ.
Итак, начнем с устной разминки:
1 задание
Какие основные тригонометрические функции вы знаете?
Иоганн БЕРНУЛЛИ – швейцарский математик, который впервые ввел современные обозначения синуса и косинуса знаками sin и cos
и cos в 1739 г. в письме к петербургскому математику Леонарду Эйлеру. Эйлер пришел к выводу, что эти обозначения очень удобны, и стал употреблять их в своих математических работах.
в 1739 г. в письме к петербургскому математику Леонарду Эйлеру. Эйлер пришел к выводу, что эти обозначения очень удобны, и стал употреблять их в своих математических работах.
Основное тригонометрическое тождество
Sin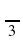 , tg
, tg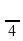 , Cos
, Cos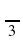 , Sinπ
, Sinπ
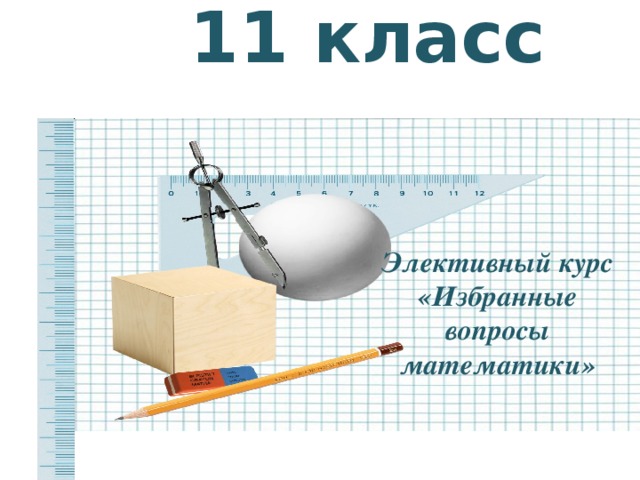
Восстановите формулы
| Sin2α |
|
|
| 2Cos2α - 1 |
| Cos (π - α) |
|
|
| 1 + tg2α |
| tgα·ctgα |
|
|
| 1 - Сos2α |
Применим данные формулы для решения заданий типа В3 и В7 из открытого банка заданий ЕГЭ
(самостоятельно с последующим обсуждением и проверкой)
2 задание
Найдите значение выражения:
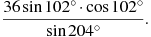
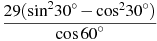
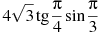
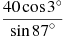
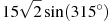
3 задание
А теперь нам предстоит вспомнить формулы для решения тригонометрических уравнений, а также частные случаи:






Основной прием решения любого уравнения - это приведение его к равносильному, более простому уравнению. Решение произвольных тригонометрических уравнения сводится к решению простейших уравнений вида sin x = a, cos x = a, tg х= a. При переходе от одного уравнения к другому пользуются общими методами решения уравнений и формулами тождественных преобразований тригонометрических выражений. Сегодня на уроке необходимо рассмотреть на примерах применение основных методов к решению тригонометрических уравнений.
4 задание
Найти ошибки в решениях тригонометрических уравнений:
 (±)
(±)  (-1k)
(-1k)
 (πk)
(πk)  (πk)
(πk)
5 задание
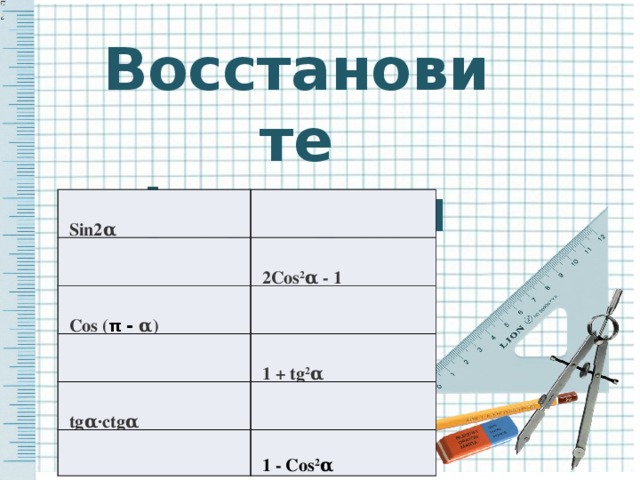
Решение уравнений с взаимопроверкой:
1. sin x = 0
2. cos x = -1
3. cos 3x = -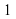 /2
/2
4. sin 0,5x = 1
5.tg 4х = 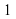
После истечения времени ученики меняются тетрадями и проверяют работу соседа. При оценке работы учитывается не только правильность выполнения работы, но и количество выполненных заданий.
Ответ:
1. х =πк, кЄZ
2. х =π + 2πк, кЄZ
3. х = +2π/9 + 2πк/3, кЄZ
4. х = π + 4πк, кЄZ
5. х = π/16 + πк/4, кЄZ
Динамическая пауза.
Самомассаж (по системе М.С. Норбекова)
Аутомануальный комплекс (массаж)
Разогреть ладони энергичным потиранием. Указательными пальцами осуществлять вкручивающие движения по часовой и против часовой стрелке – 6-8 раз в каждую сторону.
• Точка на лбу между бровями.
• По краям крыльев носа.
• В среднюю линию между нижней губой и верхним краем подбородка.
• В височной ямке (парные).
• Чуть выше роста волос под основанием черепа.
Массаж ушных раковин
Каждое упражнение выполнять 6 – 8 раз.
• Потягивание ушных раковин сверху вниз.
• Потягивание ушных раковин снизу вверх.
• Потягивание ушных раковин назад.
• • Потягивание ушных раковин в стороны.
• Круговые движения по часовой стрелке.
• Круговые движения против часовой стрелке.
Разогреть ушные раковины, чтобы они «горели» с умеренной силой.
Гимнастика для глаз
Каждое упражнение выполнять 6 – 8 раз.
• Движение глаз по горизонтальной линии вправо-влево.
• Движение глаз по вертикальной линии вверх-вниз.
• Круговые движения открытыми глазами по часовой и против часовой стрелке.
• Сведение глаз к переносице, затем смотреть в даль.
• Сведение глаз к кончику носа, затем смотреть в даль.
• Сведение глаз ко лбу, затем смотреть в даль.
• Упражнение на аккомодацию.
• Положить ладони на закрытые глаза, сделать резкий глубокий вдох через нос, затем выполняем медленный выдох через рот, через 20-30 секунд убираем ладони и открываем глаза.
Упражнения для шейного отдела позвоночника
Каждое упражнение выполнять 6 – 8 раз.
• Скольжение подбородком по грудине вниз.
• «Черепаха»: наклоны головы вперёд-назад.
• Наклоны головы вправо-влево.
• «Собачка»: вращение головы вокруг воображаемой оси, проходящей через нос и затылок.
• «Сова»: поворот головы вправо-влево.
• «Тыква»: круговые движения головой в одну и другую сторону.
Упражнения для верхнего грудного отдела позвоночника
Каждое упражнение выполняем 6 – 8 раз.
• «Нахмурившийся ёжик»: плечи вперёд, подбородок к груди; плечи назад, голову назад.
• «Весы»: левое плечо вверх, правое вниз. Поменять положение рук.
• Поднимание и опускание плеч вверх и вниз.
• Круговые движения плечами вперёд и назад.
• «Пружина»: вытягивание позвоночника, сжимание позвоночника.
• Скрутка позвоночника: поворот плеч вправо-влево
Великий физик, математик и политик А. Эйнштейн заметил: «Мне приходиться делить время между политикой и уравнениями. Однако, уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Если вы знаете свойства тригонометрических функций, их значения, формулы тригонометрии, то с решением не будет никаких трудностей.
Решение более сложных тригонометрических уравнений состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения. Какие методы преобразования вам известны?
Решение уравнений методом разложения на множители.
Приведение данного уравнения к квадратному относительно одной тригонометрической функции с последующей заменой переменной и подстановкой. Алгебраический метод.
Решение однородных уравнений первой и второй степени. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла.
Рассмотрим каждый из перечисленных методов на примерах.
1) Решить уравнение: 2 sin x · cos 5x – cos 5x = 0.
Решение:
сos5 x (2sin x – 1) = 0 ,
1) sin x = 1/2 , 2) cos 5x = 0 ,
х = (-1)kπ/6 +πk, k Є Z. х = π/10 + πn/5, nЄZ
2) Решить уравнение: 2 cos2x + 3 sin x = 0.
Решение:
т. к. cos2x = 1 - sin2x,
2(1 - sin2x) - 3 sin x = 0,
2 sin2x - 3 sin x - 2 = 0.
sin x = t, t = -1/2, t = 2
sin x =-1/2 или sin x = 2-решений не имеет
х = (-1)k arcsin(-1/2)+πk
x = (-1)k+1π/6 +πk, k Є Z.
3) Решение однородных уравнений первой и второй степени.
Однородными называются уравнения вида a·sinx+b·cosx = 0 - первой степени,
a·sinx+ b·sinx·cosx+c·cosx = 0 - второй степени и т.д., где a, b, c - числа.
Однородные уравнения любой степени решаются делением на подходящую степень cosx или sinx.
Решить уравнение: sin x - 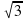 cos x = 0.
cos x = 0.
Решение: sin x - 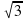 cos x = 0, разделим обе части уравнения на cos x
cos x = 0, разделим обе части уравнения на cos x
tg x - 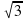 = 0
= 0
tg x = 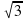
х = π/3 + πn, nЄZ
Выберите среди данных уравнений однородное
уравнение первой степени и решите его:
сos x – sin 3x = 0; 2) cos x – 3sin x = 0;
3) cos x – 3sin x = 2; 4) cos² x – 3sin x = 0.
cos x – 3sin x = 0 Ответ: arctg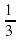 + πn, n
+ πn, n Z
Z
1 уровень
Самостоятельная работа.
Решить уравнения:
1.8 cos2x – 6 cos x – 5 = 0.
2. sin2x + sinx = 0.
3. sinx – cosx = 0.
4. sinx + cosx = 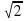 .
.
2 уровень
Вы освоили решение уравнений 2 уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных ситуациях.
Достаточно часто в задачах на решение тригонометрических уравнений и систем требуется указать не общее решение, демонстрирующее бесконечное семейство корней, а выбрать только несколько из них, которые лежат в определенном диапазоне значений.
На этом основаны решения заданий ЕГЭ типа С1
![]()
![]()

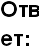
![]()
![]()
![]()
а)
![]()
б)
Подведем итог урока.
Мне хочется еще раз обратиться к словам Конфуция. Сегодня нам пришлось и размышлять, и подражать, и применять свой опыт при преобразовании тригонометрических выражений. И все эти пути, действительно, ведут к новым знаниям.
Итак, мы повторили основные методы решения тригонометрических уравнений. Дома необходимо решить уравнения, разделяя их по методам решения.
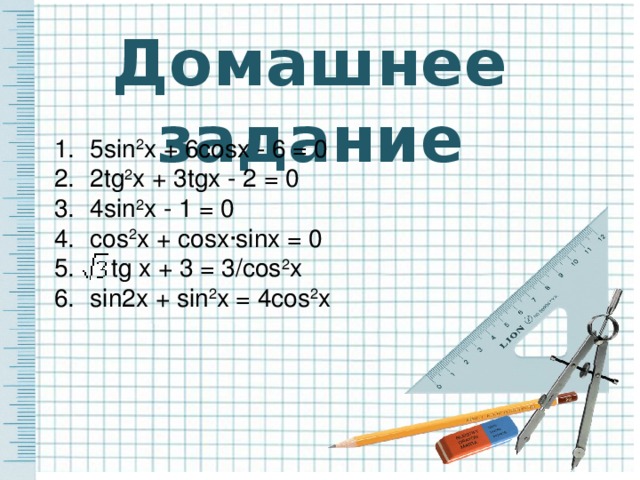
Решите уравнения:
5sin2x + 6cosx - 6 = 0
2tg2x + 3tgx - 2 = 0
4sin2x - 1 = 0
cos2x + cosx·sinx = 0
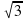 tg x + 3 = 3/cos2x
tg x + 3 = 3/cos2x
sin2x + sin2x = 4cos2x
Вопрос классу: «Оцените своё самочувствие на уроке, поставив какой-либо значок на графике функции у = sin х, изображенной на доске. Где вы себя ощущали: на гребне волны синусоиды или во впадине?
Хочется закончить урок словами Я.А.Коменского: “ Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию ”.

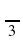
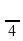

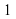 /2
/2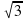
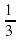 + πn, n
+ πn, n Z
Z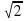 .
.