Сценарий урока геометрии в 8 классе по теме «Описанная окружность»
Цель урока: создание целостного представления о том, как описать окружность вокруг многоугольника.
Задачи: 1) рассмотреть определение окружности, описанной около
многоугольника;
2) доказать теорему об окружности, описанной около треугольника;
3) определить, что является центром окружности, описанной около
треугольника;
4) выявить, около любого ли четырёхугольника можно описать
окружность
Ход урока:
- Подход к новой теме
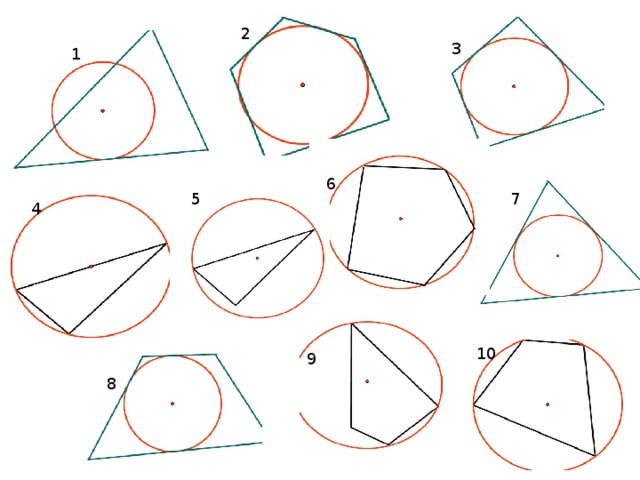
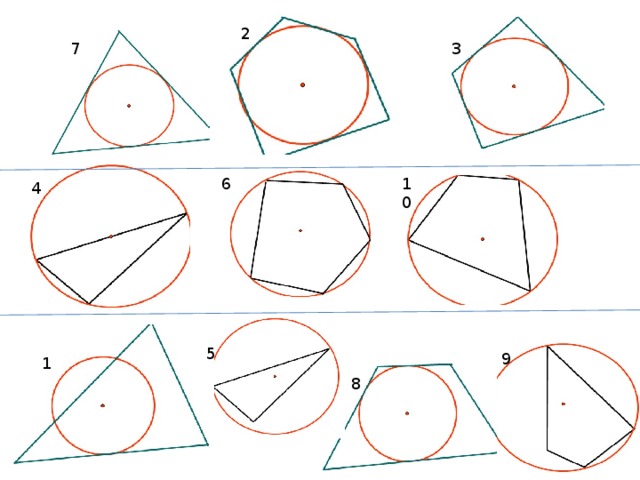
(слайд1) Разбейте на группы данные рисунки, дав каждой выделенной группе соответствующее название. (слайд2)Какую тему мы рассмотрели на предыдущем уроке? Какая нас ожидает сегодня?(слайд 3)
Что мы знаем о вписанной окружности?( определение, теорему о вписанной в треугольник окружности, что является центром вписанной в треугольник окружности и когда в четырёхугольник можно вписать окружность)-слайды4-6. Всё это можно узнать и об описанной окружности. А значит, какие задачи мы ставим перед собой на этом уроке?
(записать их на доске)
- Основная часть урока.
Итак, начинаем реализовывать наши задачи. Первая из них – определение окружности, описанной около многоугольника.
Сначала выполним задание такое( слайд 7)Выбираете свой уровень сложности. Даю минуту на обдумывание, после чего делимся надуманным(спросить представителей всех уровней, начиная с слабого. После всех ответов определение вынести на доску-слайд 8).
(слайд9-вопрос). Попробуйте ответить на него. Это наше предположение. Но мы же в геометрии не верим на слово, а должны это доказать. Задание следующее(слайд 9).Каков ваш выбор? На это задание время даю больше, итогом вашей самостоятельной работы должно быть выполненноезадание.
(слайд 10)-используем рисунок для доказательства теоремы. Итак, что мы доказываем?
(слайд 11). предлагаю вам очередное задание-слайд 12. Кому требуется подсказка, поднимайте руку.
После выполненного задания отвечаем на поставленный вопрос. Итак, вывод?.(подтверждение этого-слайд 13).
(слайд 14 –вопрос) Для ответа на этот вопрос выполним задание(слайд 14). Итак, кто готов отвечать?
- Итог урока: Мы почти закончили работу на уроке. Осталось подвести итоги. Обратимся к тем задачам, которые мы сформулировали в начале урока. Ответьте на них письменно в тетради. Кто желает прочитать, что у него получилось?.
- Домашнее задание: Кто ответил правильно на все вопросы, поставленные в начале урока - №702(а),№708,
остальным- повторить весь материалурока по учебнику(стр.175,176) и составить вопросы по теме одноклассникам.
Просмотр содержимого документа
«Кроссворд»
Просмотр содержимого документа
«Сценарий урока геометрии в 8 классе по теме»
Сценарий урока геометрии в 8 классе по теме «Описанная окружность»
Цель урока: создание целостного представления о том, как описать окружность вокруг многоугольника.
Задачи: 1) рассмотреть определение окружности, описанной около
многоугольника;
2) доказать теорему об окружности, описанной около треугольника;
3) определить, что является центром окружности, описанной около
треугольника;
4) выявить, около любого ли четырёхугольника можно описать
окружность
Ход урока:
Подход к новой теме
(слайд1) Разбейте на группы данные рисунки, дав каждой выделенной группе соответствующее название. (слайд2)Какую тему мы рассмотрели на предыдущем уроке? Какая нас ожидает сегодня?(слайд 3)
Что мы знаем о вписанной окружности?( определение, теорему о вписанной в треугольник окружности, что является центром вписанной в треугольник окружности и когда в четырёхугольник можно вписать окружность)-слайды4-6. Всё это можно узнать и об описанной окружности. А значит, какие задачи мы ставим перед собой на этом уроке?
(записать их на доске)
Основная часть урока.
Итак, начинаем реализовывать наши задачи. Первая из них – определение окружности, описанной около многоугольника.
Сначала выполним задание такое( слайд 7)Выбираете свой уровень сложности. Даю минуту на обдумывание, после чего делимся надуманным(спросить представителей всех уровней, начиная с слабого. После всех ответов определение вынести на доску-слайд 8).
(слайд9-вопрос). Попробуйте ответить на него. Это наше предположение. Но мы же в геометрии не верим на слово, а должны это доказать. Задание следующее(слайд 9).Каков ваш выбор? На это задание время даю больше, итогом вашей самостоятельной работы должно быть выполненное задание.
(слайд 10)-используем рисунок для доказательства теоремы. Итак, что мы доказываем?
(слайд 11). предлагаю вам очередное задание-слайд 12. Кому требуется подсказка, поднимайте руку.
После выполненного задания отвечаем на поставленный вопрос. Итак, вывод?....(подтверждение этого-слайд 13).
(слайд 14 –вопрос) Для ответа на этот вопрос выполним задание(слайд 14). Итак, кто готов отвечать?
Итог урока: Мы почти закончили работу на уроке. Осталось подвести итоги. Обратимся к тем задачам, которые мы сформулировали в начале урока. Ответьте на них письменно в тетради. Кто желает прочитать, что у него получилось?.
Домашнее задание: Кто ответил правильно на все вопросы, поставленные в начале урока - №702(а),№708,
остальным- повторить весь материал урока по учебнику(стр.175,176) и составить вопросы по теме одноклассникам.
Просмотр содержимого презентации
«описанная окружность»
2
3
1
6
5
7
4
10
9
8
2
3
7
10
6
4
5
9
1
8

Тема :
Описанная окружность
Цель урока : создание целостного представления о том, как описать окружность около многоугольника
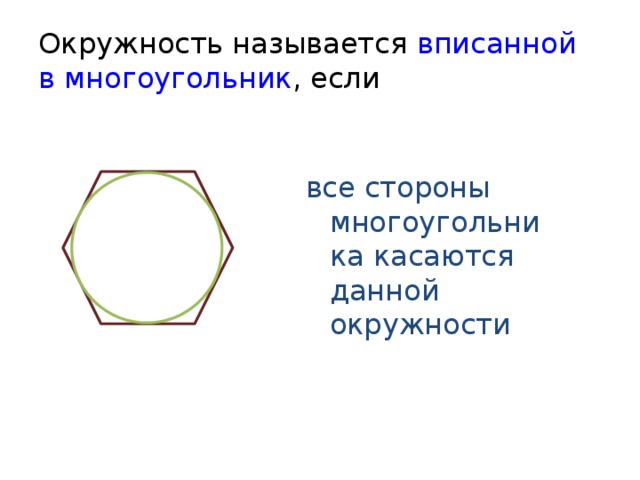
Окружность называется вписанной в многоугольник , если
все стороны многоугольника касаются данной окружности
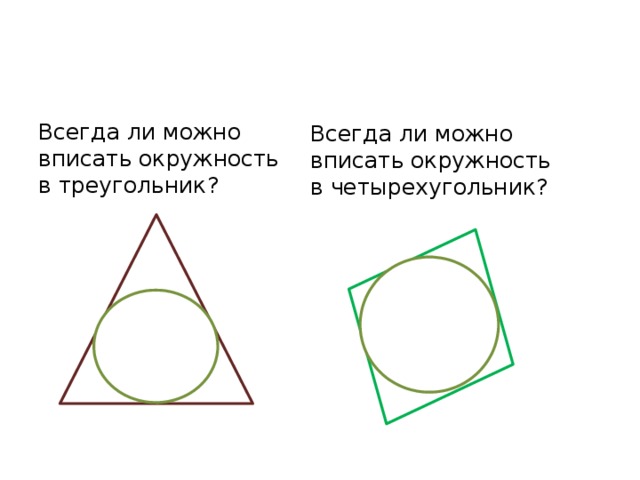
Всегда ли можно вписать окружность в треугольник?
Всегда ли можно вписать окружность в четырехугольник?
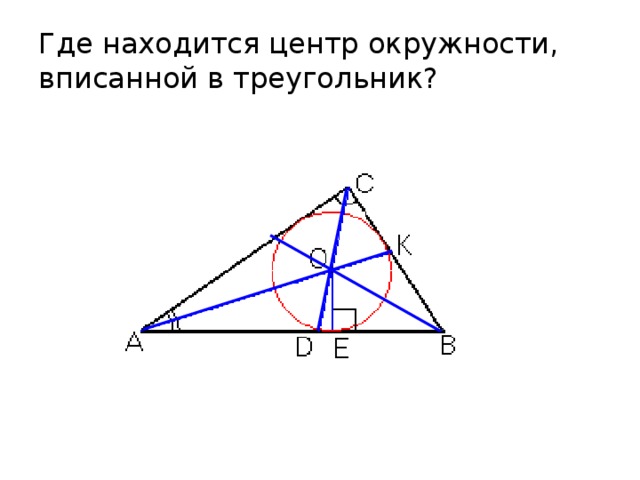
Где находится центр окружности, вписанной в треугольник?

Задание 1.
- кроссворд по теме «Окружность»( заполнить и найти в нём определение описанной окружности)
- Дать определение окружности, описанной около многоугольника
- Найти ошибку в определении:
Окружность называется описанной около многоугольника, если она соединяет все его вершины.
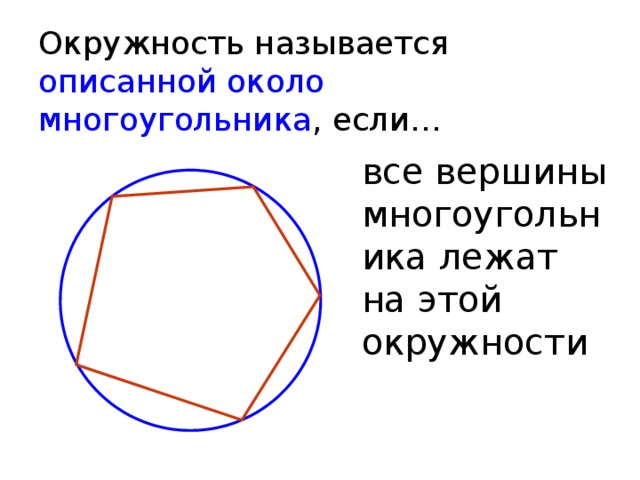
Окружность называется описанной около многоугольника , если…
все вершины многоугольника лежат на этой окружности

Около любого ли треугольника можно описать окружность?
Предположение- теорема: Около любого треугольника можно описать окружность.
Задание 2 : доказать это предположение.
- подсказка: наводящие вопросы с соответствующими рисунками(от учителя)
подсказка-план доказательства (от учителя)
Разобраться с доказательством в учебнике на стр.176
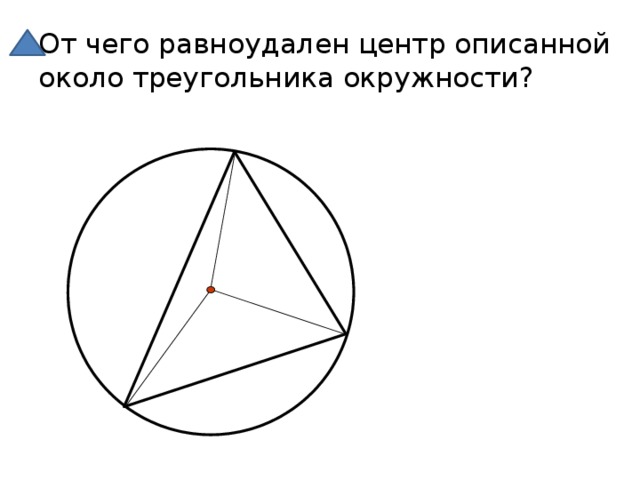
От чего равноудален центр описанной около треугольника окружности?
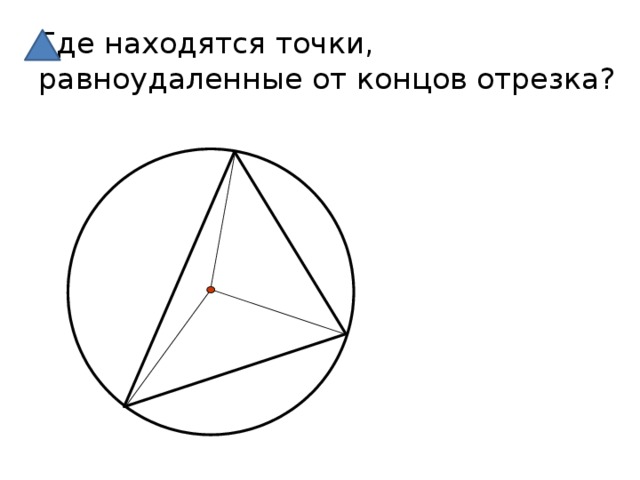
Где находятся точки, равноудаленные от концов отрезка?
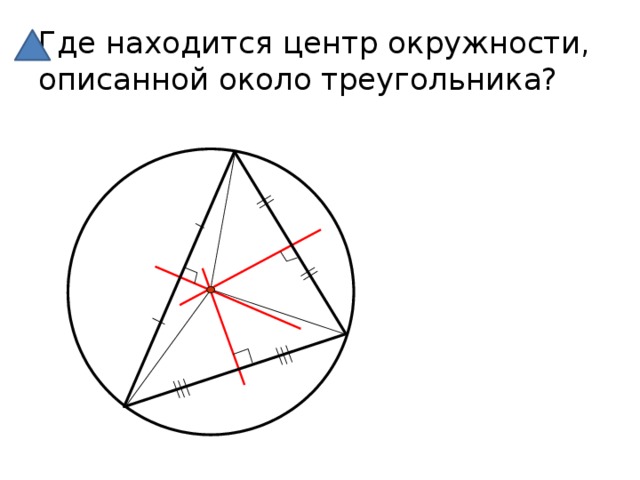
Где находится центр окружности, описанной около треугольника?
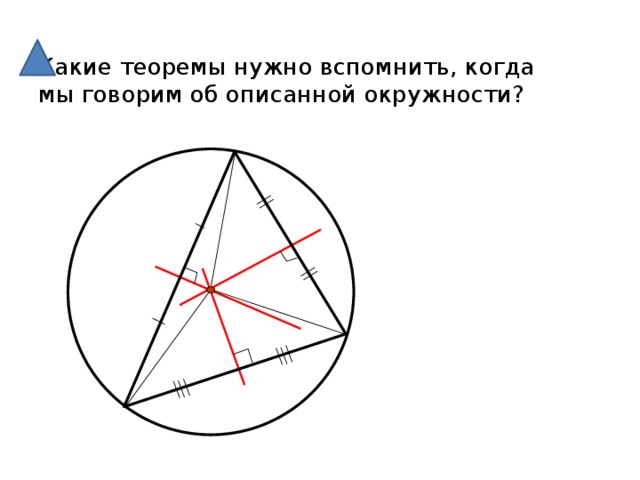
Какие теоремы нужно вспомнить, когда мы говорим об описанной окружности?

- Постройте прямоугольный треугольник
- Постройте остроугольный треугольник
- Постройте тупоугольный треугольник
Задание 3:
Опишите около построенного треугольника окружность. Сделайте вывод: где находится центр окружности, описанной около вашего треугольника?
-подсказка от учителя
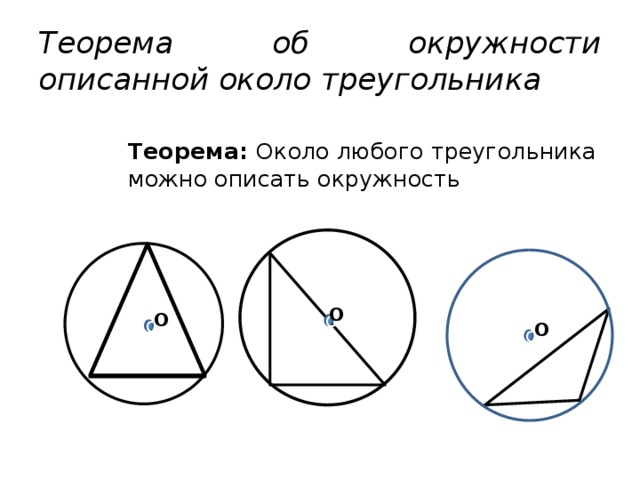
Теорема об окружности описанной около треугольника
Теорема: Около любого треугольника можно описать окружность
О
О
О
О
О
О
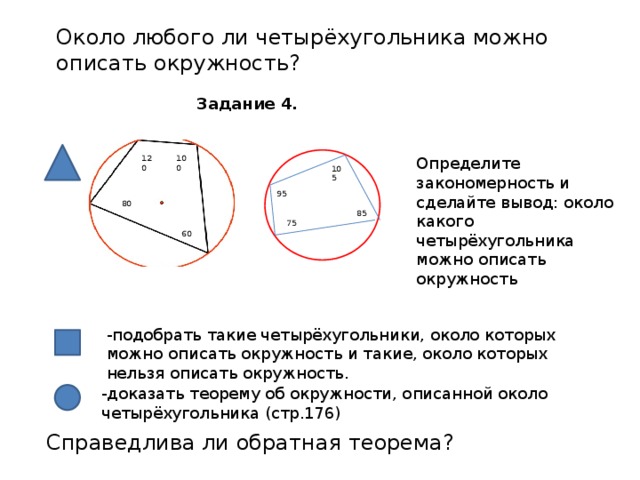
Около любого ли четырёхугольника можно описать окружность?
Задание 4.
120
100
Определите закономерность и сделайте вывод: около какого четырёхугольника можно описать окружность
105
95
80
-
85
75
60
-подобрать такие четырёхугольники, около которых можно описать окружность и такие, около которых нельзя описать окружность.
-доказать теорему об окружности, описанной около четырёхугольника (стр.176)
Справедлива ли обратная теорема?

Спасибо за работу!
 10
10

 В
В









 О
О 




































