КГУ ОШ № 117
Согласовано
Зам.директора по УВР__________Жорабаева Г.А.
Открытый урок по геометрии
в 11 «В» классе на тему:
«Объемы тел вращения»
учитель математики
Ермекбаева Г.А.
Г.Алматы, 2023г
Цель обучения –
11.3.14-знать формулу нахождения объема цилиндра и применять при решении задач
11.3.15-знать формулы нахождения объемов конуса и усеченного конуса и применять при решении задач
11.3.16-знать формулы нахождения объема шара и его частей и применять их при решении задач
Цель урока - развивать у учащихся навыки применения теоретических знаний по теме «Объём цилиндра, конуса, шара» для решения задач, выявить отношение объёмов вписанных и описанных тел вращения.
Задачи:
Образовательные: совершенствовать умения учащихся применять накопленные знания в измененной ситуации, делать выводы и обобщения; показать практическую значимость данной темы в жизни человека.
Развивающие: способствовать формированию у учащихся ключевых компетенций (сравнение, сопоставление, классификация объектов, определение адекватных способов решения учебной задачи на основе заданных алгоритмов); развитию памяти, внимания, мышления и пространственного воображения учащихся, навыков самооценки и самоконтроля; навыков творческого подхода к решению задач, исследовательской работы над задачей.
Воспитательные: способствовать развитию устойчивого интереса и созданию положительной внутренней мотивации к изучению математики; воспитанию ответственного отношения к учению.
Планируемые результаты: уметь вычислять объемы тел вращения; зная объемы вписанных фигур,найти объемы описанных фигур; не бояться решать задачи ЕГЭ, связанные с вычислением объемов тел.
Тип урока: урок применения знаний и умений учащихся.
Технологии: личностно-ориентированная, проблемно-исследовательская, индивидуально–дифференцированного обучения.
Методы обучения: словесный, наглядный, практический, частично-поисковый, проблемный.
Формы работы: индивидуальная, фронтальная, работа в парах, групповая.
Оборудование и материалы для урока: компьютер, интерактивная доска, презентация, раздаточный материал, геометрические фигуры.
Девиз урока: «Дорогу осилит идущий, а математику – мыслящий».
Ход урока.
1.Организационный момент : Приветствие. Проверка готовности к уроку.
2.Вызвать к доске 3 учеников, чтоб подготовиться ответить на вопросы : 1) конус
2)цилиндр
3) шар
Пока они готовятся, провести математический диктант.
Математический диктант:
-Выберите лишнее
а) квадрат, прямоугольник, цилиндр;
б) призма,конус, параллелепипед;
в) шар, треугольник, параллелограмм.
ответ: цилиндр, конус, шар.
Учитель: Как вы догадались, тема нашего урока будет связана с этими фигурами.
-как по другому их можно назвать?
( тела вращения)
-вращением каких фигур получаем цилиндр, конус, шар?
(прямоугольника, треугольника, окружности)
-тема нашего урока «Объемы тел вращения»
- откройте тетради и напишите число и тему нашего урока.
-но вначале вспомним, что это за фигуры.
(слушаем ответы детей у доски)
3. На доске написать 3 формулы : 1) V =13 Sоснн
2) V =Sоснн
3) V =43π R3
И названия фигур :пирамида, прямая призма,конус, цилиндр,, наклонная призма, шар,прямоугольный параллелепипед, куб.
-написать в тетрадях объемы каких фигур можно вычислить по первой, второй и третьей формулам?
Ответ: 1) пирамида, конус;
2) цилиндр, прямая призма, наклонная призма, прямоугольный параллелепипед, куб;
3) шар
Разбиваем класс на 4 группы и решаем задачи по группам.
Задание 1:
-Найдите объем конуса с высотой 3 см и диаметром 8 см.
-Найдите объём цилиндра, если диаметр его основания равен 10 см., а высота цилиндра 12 см.
- Найдите объём шара, диаметр которого равен 12 см.
Задание 2:
1 группа: В цилиндр вписан шар радиуса 2. Найдите отношение объёмов цилиндра и шара
2 группа: В цилиндр вписан шар радиуса 3. Найдите отношение объёмов цилиндра и шара
3 группа: В цилиндр вписан шар радиуса 4. Найдите отношение объёмов цилиндра и шара.
4 группа: В цилиндр вписан шар радиуса 5. Найдите отношение объёмов цилиндра и шара.
( пока все решают,вызвать одного ученика к доске решить задачу : найти отношение объёма цилиндра к объёму вписанного в него шара)
-Давайте посмотрим, что у вас получилось?
Учитель записывает на доске результаты.
-Чему равно отношение объёма цилиндра к объёму вписанного в него шара?
Гипотеза: отношение объёма цилиндра к объёму вписанного в него шара равно3:2.
-А теперь проверим так ли это на самом деле.( Проверить доказательство утверждения в общем виде записать в тетрадях).
- В любой цилиндр можно вписать окружность?
Вывод: Мы доказали теорему Архимеда: «Объём равностороннего цилиндра в полтора раза превышает объём вписанного в него шара».
Устно.
-Объём шара вписанного в цилиндр равен 40см3. Чему равен объём цилиндра? (Ответ: 60 см3)
-Объём цилиндра равен 120. Найдите объём вписанного в него шара.( Ответ: 80.)
Задание 3:
-Рассмотрим ещё одну зависимость объёмов тел вращения.
1 группа. Цилиндр и конус имеют общее основание и высоту. Вычислите объем цилиндра, если объем конуса равен 32.
2 группа. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем конуса, если объем цилиндра равен 60куб см.
3 группа. Цилиндр и конус имеют общее основание и общую высоту. Найдите объем конуса, если объем цилиндра равен 84.
4 группа. Цилиндр и конус имеют общее основание и общую высоту. Найдите объем конуса, если объем цилиндра равен 96.
.( пока все решают,вызвать одного ученика к доске решить задачу : найти отношение объёма цилиндра к объёму вписанного в него конуса)
Учитель записывает на доске результаты
Гипотеза: Если цилиндр и конус имеют общее основание и высоту, то объём цилиндра в 3 раза больше объёма конуса.
Доказательство утверждения в общем виде(записать на доске и в тетрадях)
Устно.
1.Объём цилиндра равен 30. Чему равен объём конуса с таким же основанием и высотой?
Ответ: 10.
2. Цилиндр и конус имеют общее основание и высоту. Вычислите объем цилиндра, если объем конуса равен 21.
Физминутка
1.Наклон головы вперёд-назад.
2.Наклон головы влево- вправо.
3.Описать головой полукруг.
4.Руки вперёд, кисти «замком», повороты сцепленными руками влево- вправо.
5.Руки вниз, поднимаем и опускаем плечи
Задание 4( задания ЕГЭ):
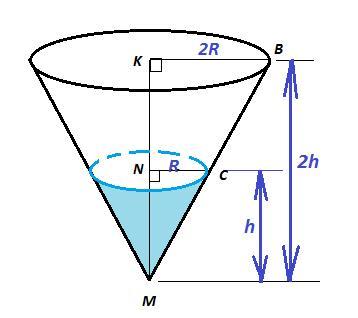
1 группа: В сосуд, имеющий форму конуса, налили 20 мл жидкости до половины высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
2 группа: В бак, имеющий форму прямой призмы, налито 10 литров воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,3 раза. Найдите объем детали. Ответ дайте в кубических дециметрах.
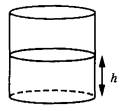
3 группа: Вода в сосуде цилиндрической формы находится на уровне h = 60 см. На каком уровне окажется вода, если её перелить в другой цилиндрический сосуд, у которого радиус основания вдвое больше, чем у данного? Ответ дайте в сантиметрах.
4 группа
“.Читал я где-то,
Что царь однажды воинам своим
Велел снести земли по горсти в кучу,
И гордый холм возвысился, - и царь
Мог с вышины с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли.”
(А.С. Пушкин “Скупой рыцарь”)
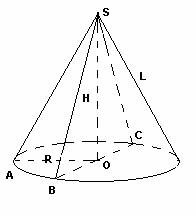
. Предположив, что численность войска составляет 100 000 человек, объем горсти равен 0,2 дм3, а угол при основании холма 450, найдите объем и высоту конуса.
Ответ: 2,7 м
-Надо обладать очень богатым воображением, чтобы земляную кучу в 2,7 м ( 1,5 человеческих роста) назвать «гордым холмом». Сделав расчет для меньшего угла, мы получили бы еще более скромный результат.
Подведение итогов. Рефлексия.
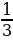 Sоснн
Sоснн R3
R3