Открытый урок по теме "Квадратные уравнения. Виды и способы решения"

Тема: Квадратные уравнения. Виды и способы решения. (Урок путешествие).

Подготовила: Фисенко Т.В. - учитель математики МБОУ «СОШ № 92», г. Кемерово.

Эпиграф к уроку: "Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным".

Паскаль

Цели:

1. Усвоить понятие квадратного уравнения, неполного квадратного уравнения.
   Получить приемы решения неполных квадратных уравнений.
   Уметь находить корни неполных квадратных уравнений.

2. Развитие вычислительных навыков: навыков решения квадратных уравнений с помощью формул, навыки нахождения дискриминанта квадратного уравнения, развитие логического мышления,

3. Способствовать рациональной организации труда, внимательность, активное участие в учебно-познавательном процессе, самостоятельность, самокритичность.

Оборудование к уроку: компьютер, проектор, карточки.

План урока

1. Организационный момент "Настроимся на урок!" (Знакомство с планом работы на уроке)

2. Теоретический опрос на понятие квадратного уравнения. Самостоятельные выводы на вопрос «Каким может быть неполное кв. уравнение?»

3. Работа в парах по карточкам: самостоятельно решить предложенные неполные уравнения, с дальнейшей проверкой на доске.

4. Историческая справка.

5. Фронтальная работа с классом.

6. Самостоятельная работа.

7. Итог.

Ход урока

1. Организационный момент "Настроимся на урок!" (Слайд 1,2)

Здравствуйте, ребята и гости нашего урока! Математику не зря называют "царицей наук", ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики - любознательность. Постараемся доказать это на уроке. Мы с вами начали изучать новый большой раздел «Квадратные уравнения».

Эпиграфом к уроку я взяла слова великого математика Паскаля "Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным". Что перед вами? О каком событии говорят коэффициенты уравнения? (Дата, когда олимпийский огонь будет в нешем городе). ( Слайд 3,4,5)

2. Давайте вспомним. Станция теоретическая. (Слайд 6)

Какой вид имеет квадратное уравнение?

Сколько решений имеет полное квадратное уравнение? От чего это зависит? (Слайд 7)

1. Работа в парах.

Ребята, а теперь давайте вместе с вами придем окончательно к выводу: «Какой вид могут иметь неполные квадратные уравнения?» Выслушать мнение ребят, подвести итог. (Слайд 8)

Ученики получают карточки с заданиями. Решают предложенные уравнения, первые называют ответ, далее проверка на экране. (Слайд 9- 11)

1. Историческая справка. Станция историческая. (Слайд 12-15)

По словам математика Лейбница, "кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет".

Ученик заранее готовит сообщение об истории квадратных уравнений, с презентацией.

Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение при решении различных тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств, большого количества разных типов задач.

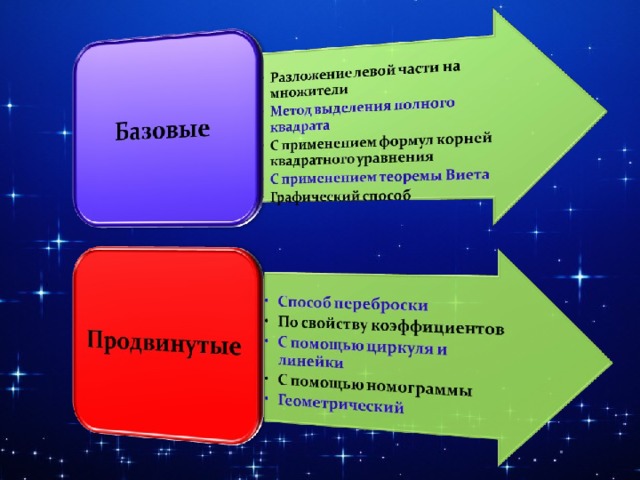
В школьном курсе математики подробно изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. В математической науке есть десять способов решения квадратных уравнений.

Способы решения квадратных уравнений, изучаемые в школе:

• Разложение левой части на множители

• Метод выделения полного квадрата

• С применением формул корней квадратного уравнения

• С применением теоремы Виета

• Графический способ

Продвинутые способы решения квадратных уравнений:

• Способ переброски

• По свойству коэффициентов

• С помощью циркуля и линейки

• С помощью номограммы

• Геометрический

5 Фронтальная работа.

Итак ребята, вы добрались до станции «Тренажерной». Перед тем как приступить к самостоятельной работе поработаем все вместе. (Слайд 16).

1. Самостоятельная работа по карточкам.

Учащимся выдаются карточки на два варианта. После выполнения, ответы вводятся на экране. (Слайд 17)

7. Итог урока. Станция «Конечная». (Слайд 18)

Учитель:

Что нового мы узнали на уроке?

Какое уравнение называется квадратным?

Какие виды квадратных уравнений вы знаете?

Момент рефлексии: учащимся предлагается ответить на вопросы:

Что понравилось мне сегодня на уроке?

В чем я испытывал затруднения?

Сегодня мне удалось…

И закончить сегодняшний урок хотелось бы словами великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»

Оценивание учащихся. Сообщение домашнего задания. (Слайд 19).

Домашнее задание и номера выполняемые в классе соответствуют учебнику «Алгебра 8», автор С.М. Никольский, М.К. Потапов и др.

Тема урока:

Квадратные уравнения. Виды и способы решения.

Цель урока:

Изучить и обобщить знания и умения учащихся в решении квадратных уравнений, выработать умения выбрать рациональный способ решения, способствовать развитию умения видеть и применять изученные закономерности в нестандартных ситуациях.

Что перед вами? О каком событии говорят коэффициенты уравнения? 30x ²+11x+2013=0

Урок посвящен одному из ярких и выдающихся событий нашей страны - Сочинской олимпиаде в феврале 2014г. Это особенное событие, долгожданное для всех жителей России. В относительно короткие сроки были возведены олимпийские объекты. Разработаны и построены олимпийские трассы. Но прежде чем все это было воплащенно в жизнь строителями и современной техникой, инженеры должны были произвести грамотные расчеты, основываясь на математических знаниях.

Сегодня мы так же как и олимпийский огонь совершим путешествие прямо в кабинете математики в различные уголки нашей «Школьной страны». Цель нашего путешествия как можно больше узнать о видах квадратных уравнений и о способах их решений.

И так, лично я уже готова отправиться в путешествие, но перед этим вы должны познакомиться с маршрутным листом.

1. Станция «Теоретическая»

4. Станция «Конечная»

2. Станция «Историческая»

3. Станция «Тренажёрная»

Станция «Теоретическая»

• Сформулируйте определение квадратного уравнения.

2. Объясните, в чём заключается смысл ограничения в определении квадратного уравнения (а ≠ 0).

3. Какое уравнение будет называться неполным?

Определение: квадратное уравнение называется не полным, если у него коэффициенты b=0 или c=0.

0 D = 0 D Два корня Один корень Уравнение не имеет Х 1 , 2 = - b ± действительных Х = - b корней 2а 2а Коль минус с тобою мы замечаем, То это радует даже лентяя. Тогда уравненье корней не имеет, И прекращается сразу решенье." width="640"

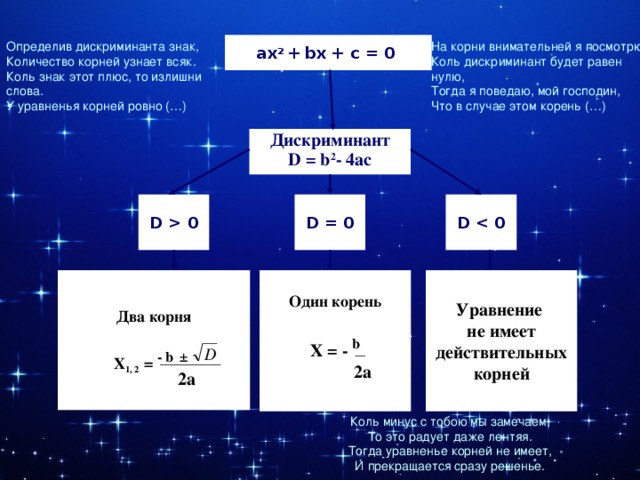
На корни внимательней я посмотрю,

Определив дискриминанта знак,

ах 2 + bх + с = 0

Коль дискриминант будет равен нулю,

Количество корней узнает всяк.

Тогда я поведаю, мой господин,

Коль знак этот плюс, то излишни слова.

Что в случае этом корень (…)

У уравненья корней ровно (…)

Дискриминант

D = b 2 - 4ac

D 0

D = 0

D

Два корня

Один корень

Уравнение

не имеет

Х 1 , 2 = - b ±

действительных

Х = - b

корней

2а

2а

Коль минус с тобою мы замечаем,

То это радует даже лентяя.

Тогда уравненье корней не имеет,

И прекращается сразу решенье.

Неполные квадратные уравнения:

Если , то корней нет.

Если ,то

Например:

Вывод: данное уравнение решений не имеет.

Например:

Составьте правильный ход решения каждого уравнения:

• x 2 -25=0,
• x 2 -3x=0,
• x 2 +16=0.

а) x(x-3)=0,

б) x 2 = -16,

в) (x-5)(x+5)=0,

г) x-5=0,

д) x-3=0,

е ) x+5=0 .

Что будет являться решением каждого из уравнений:

а) решений нет,

б) x = -5,

в) x = 3,

г)x = 5,

д) x = 0.

Станция «Историческая»

.

-

Впервые ввёл термин «квадратное уравнение» немецкий философ

Кристиан Вольф.

Вывод формулы решения квадратного уравнения  в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 в. благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид. 

.

Сильвестр Джеймс

Джозеф

Михаэль Штифель.

В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов произвел в 1544 году немецкий математик – Штифель

Это было настоящее событие в математике.

английский математик, который ввёл термин «дискриминант».

Станция «Тренажёрная»

• Работа со всем классом:

№ 210 а-з; № 211а,б,г,д; № 224 л.ст.

• Самостоятельная работа, с последующей самопроверкой.

Правильные ответы:

• В-1

• В-2

• 1. -1
• 2. 0
• 3. 1
• 4. -47
• 5. 2
• 6. -1

• 1. 1
• 2. 0
• 3. 2
• 4. 256
• 5. 2
• 6. -1,5

Станция «Конечная»

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н.э. вавилоняне.

В наше время невозможно представить себе решение как простейших , так и сложных задач не только в математике, но и в других точных науках , без применения решения квадратных уравнений.

Надеюсь наш урок принес для каждого из Вас свои результаты.

Домашнее задание

Пункт: 4.3; 4.4. №: 213; 214; 225;231.

До новых встреч!

Желаю творческих успехов.