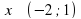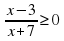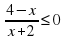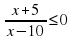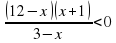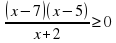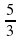І Неполные квадратные уравнения вида х2 =d.
Решение: x= ±√d;
Примеры:
X2 =4, x=±√4 =±2;
Y2 = 16, y=±√16=±4;
Z2 = 49 /64, z= ±√49/64 = ±7/8;
X2 = 5, x= ±√5;
m2= -1, не имеет решения, так как квадрат любого числа, отличного от нуля, есть число положительное.
Реши самостоятельно:
n2 = 0
_______________________________________________________________________________
-3x2 =0
________________________________________________________________________________
5x2 = 0
_________________________________________________________________________________
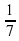 x2 = 0
x2 = 0
_________________________________________________________________________________
x2 = 1
_________________________________________________________________________________
y2=81
_________________________________________________________________________________
z2 = 7
_________________________________________________________________________________
m2 =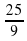
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
|
|
|
ІІ Неполные квадратные уравнения
Вида ax2 +c =0, c≠0.
Решение:1) ax2= -c /:a
X2= -c/a
X =±√-c/a, с
Примеры:
8x2 – 72 =0 2) 2y2 +32 = 0
8x2 =72 /:8 2y2 =- 32/ :2
X2 = 9 y2 = -16
X = ±√9 =±3 не имеет решения
Реши самостоятельно:
X2 – 64 =0
________________________________________________________________________
аблица для ответов:_____________________________________________________________X2 – 36 =0
_____________________________________________________________________________________________________
X2 + 81 =0
________________________________________________________________________
3X2 – 15 =0
________________________________________________________________________
4X2 – 64 =0
________________________________________________________________________
4X2 –1 69 =0
________________________________________________________________________
25X2 – 1 =0
________________________________________________________________________
3X2 =15
________________________________________________________________________
2X2 = 1/8
________________________________________________________________________
2X2 + 18 =0
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
|
|
|
ІІІ Неполные квадратные уравнения вида ax2 + bx = 0, b≠ 0.
Решение: x (ax + b) =0,
x= 0, ax +b =0
ax = -b,
x = -b /a
Ответ: 0; -b /a
Примеры:
x2 -7x =0 2)5x + x2 = 0 3)6 x2 -x =0
x(x-7) =0 x(5+x) = 0 x (6x -1) =0
x=0, x-7 = 0 x=0, 5+x =0 x=0, 6x-1 =0
x=7 x = -5 6x =1/ :6
Ответ: 0; 7. Ответ: 0; -5. x = 1/6
Ответ: 0; 1/6.
Реши самостоятельно:
x2 -9x =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
y2 -7y =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
z2 +6z =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9x2 -x =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7y2 -y =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6z2 +z =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2x2 +5x =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
8x2 -16x =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9)3x2 -3/5 x =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
10)-8x2 + 16x =0
для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
|
|
|
|
|
Iᴠ Решение квадратных уравнений вида ax2 + bx +c =0,
Определить количество корней:
Найдём значение дискриминанта по формуле: D = b2 – 4ac;
Если D 0, то уравнение имеет два различных корня;
Если D
Если D = 0, один корень.
Примеры:
x2 -4x -5 =0
a = 1, b = -4, c = -5,
D = (-4)2 – 4*1*(-5) = 16 + 20 = 36 0, уравнение имеет два различных корня;
5x2 -2x + 4 =0
a= 5, b = -2, c= 4
D = (-2)2 -4*5*4 =4 – 80 = -76 не имеет корней
x2 -4x + 4 =0
a =1, b=-4, c = 4,
D= (-4)2 -4*1*4 =16 -16 = 0, один корень, или (x-2)2 =0, x=2
Реши самостоятельно:
2x2 -7x + 3 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2x2 -3x + 11 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
x2 -10x + 25 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4)3 x2 + x -10 =0
___________________________________________________________________________________________________________________________________________________________________________________________________________ _______________________________________________________________________________________________________
5)-2 x2 -3x + 1 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6)-x2 + 2x - 10 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7)x2 + 6x + 9 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
8)5x2 - x - 6 =0
______________________________________________________________________________________________________________________________________________________________________________________________________________
9)-5x + x2 + 6, 25=0
__________________________________________________________________________________________________________________________________________________________________________________________________
10)-x2 -7x -15 =0
_______________________________________________________________________________________________________________________________________________________________________________________________________________
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
|
|
|
|
|
V Решение квадратных уравнений вида ax2 + bx +c =0,
Найти корни квадратного уравнения.
D = b2 – 4ac;
X1,2 =(-b ±√D): 2a или 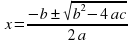
Примеры:
2x2 -5 x - 3 =0
A =2, b=-5, c= -3,
D =………………………………………….. =49 0,
X1,2 =(-(-5) ±√49) :2*2 = (5±7): 4; x1 =12:4 =3, x2 = -2 :4 = -0,5;
Ответ:-0,5; 3.
Реши самостоятельно:
1)3x2 -2 x - 8 =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________
2) 9x2 -6 x + 2 =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________
3) 2x2 -7 x - 15 =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________
4) 3x2 +5 x + 2 =0
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
____________________________________________________________________________________________________
5) 5x2 -12 x + 4 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6) 3x2 -5 x + 2 =0
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
7) 4x2 -6 x + 2 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
8) 17x2 + 3 x - 20 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
9) 1000x2 -2 x - 998 =0
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
10) 15x2 -19 x + 4 =0
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
|
|
|
|
|
VI. Приведённое квадратное уравнение
X2 +px + q =0
По обратной теореме Виета: пусть x1, x2 - корни квадратного уравнения,
x1 +x2 = -p,
x1 * x2 = q
Пример:
1) x2 - 5x + 6 =0
x1 +x2 = 5,(1) Так как x1 * x2 0, то x1 0, x2 0 или x1 x2
x1 * x2 = 6,(2) Так как x1 +x2 0, то x1 0, x2 0
Подбираем: 6= 1*6, но 1+6 =7 не удовлетворяет x1 +x2 = 5
6 = 2*3 и 2 +3= 5, удовлетворяет x1 +x2 = 5
Ответ:2; 3.
Реши самостоятельно:
1) x2 + 4x - 12 =0
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2) x2 + 2x -15 =0
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3)x2 + 8x + 12 =0
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4) x2 - 7x + 12 =0
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
5) x2 - 11x + 24 =0
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
VІI. Решение квадратных уравнений.
Пример:
x2 + 2x = 2x2 – 7x,
x2 + 2x - 2x2 + 7x = 0
-x2 + 9x = 0
-X(x -9) = 0
X= 0, x-9 =0
X=9
Ответ:0; 9.
Реши самостоятельно:
-x - 2x = 3x2 + 5x2,
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
x2 - 4x = 2(5– 2x),
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
15+ 3(x+1) = x2 + 3x,
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
12 - 2(x+ 4) = x2 – 2x,
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
X2+ (x- 1) = 9 – x2,
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
VІІI. Решение квадратных неравенств с помощью графика квадратичной функции
ax2 + bx +c 2 + bx +c 0,(≥0);
Решение: ax2 + bx +c =0,
D
X1, x2
Наносим корни квадратного трёхчлена на координатную прямую:

+
+
+
+
+
x1
x2



__-
x2

_
x1
x2
Если старший коэффициент a0, то ветви параболы направлены вверх.

 Пример: решить неравенство: x2 - 7x + 12
Пример: решить неравенство: x2 - 7x + 12
Решение: x2 - 7x + 12 =0 +
+



 1)D =1; 2) x1 =4;x2 =3; 3)
1)D =1; 2) x1 =4;x2 =3; 3) __
a0, ветви вверх; знак неравенства 3
4
знаку «
Ответ: (3;4). Так как точки выколотые, то скобки круглые.
Реши самостоятельно:
3x2 - 4x + 1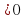
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2) - 9x2 - 7x + 16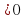
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3) -x2 + 15x - 14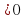
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4) 2x2 - 7x + 3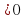 __________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
5)x2 + 6x + 9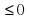
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
ІX. Решение неравенств методом интервалов
Пример 1
(x+ 5)(x-4) 0
1)Найти значения х, при которых левая часть равна нулю:
Х1 = -5, х2 =4, т. е. (-5 +5)(4-4)
2) полученные значения отметить на координатной прямой:

1
2
3
3)Выбрать число из каждого промежутка (интервала) и подставить в исходное неравенство, определяя знак «+» или «-».
Например, из первого интервала выберем число 5,
Подставим вместо х в неравенство, получим:(5+5)(5-4) =10 0, значит, в первом интервале ставим знак «+»
Из второго – можно выбрать 0, получим: (0+5)(0-4) = -20
Аналогично работаем с третьим интервалом.
4) Так как знак неравенства , то решению неравенства соответствуют промежутки со знаком «+»
5) Ответ: х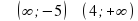
Форма скобок зависит от знака неравенства.(смотри ранее)
Пример 2
(3х+8)(х-7)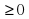
Решение:
1) 3х+8 =0 х-7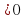
3х =-8/: 3 х = 7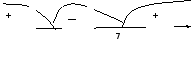
Х =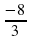
Ответ: х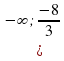 ]
]
Реши самостоятельно:
1)(2-х)(х-3)________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2)(7x-4)(4+7x)≤0
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3)(3x+2)(5-x)0
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4)(2x-1)(2x+1)≤0
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
Х Решение дробно – рациональных неравенств
Алгоритм решения:
1) нули числителя;
2) нули знаменателя;
3)полученные значения нанести на координатную прямую;
4)установить знак на полученных промежутках (интервалах)
5) записать ответ.
Пример 1:
1)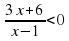 1) нули числителя: 3х+6 = 0, 3х= -6/:3, х= -2;
1) нули числителя: 3х+6 = 0, 3х= -6/:3, х= -2;
2) нули знаменателя : х-1 =0, х=1 +
+
-
 3)
3) -2
1
Ответ: 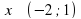
Реши самостоятельно:
1)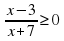
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2)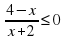
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3) 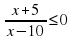
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4)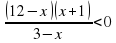
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
5)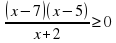
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Таблица для ответов:
Самооценка ученика:
| № зад | 1 | 2 | 3 | 4 | 5 |
| Удалось получить результат (решение, ответ)? |
|
|
|
|
|
| Правильно или с ошибкой? |
|
|
|
|
|
| Самостоятельно или с чьей-то помощью? |
|
|
|
|
|
Уважаемый, ученик!
Обобщи свои результаты в заключительной таблице, проставляя знаки «+» или «-» в каждой строке. На основании заполненной таблицы, подсчитай количество положительных и отрицательных ответов и сделай самостоятельно вывод, насколько ты владеешь теперь умением решать квадратные уравнения и неравенства. Безусловно, чем больше «+», тем в большей степени ты владеешь умениями.
Правильно выполненные задания разделов 1-7- проявления базового (минимального необходимого) уровня.
Правильно выполненные упражнения разделов 8-10 – проявление того, что овладел более сложными умениями.
Итоговая самооценка ученика:
| № раздела | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Какова была цель задания? |
|
|
|
|
|
|
|
|
|
|
| Знание алгоритма решения. |
|
|
|
|
|
|
|
|
|
|
| Знание формул. |
|
|
|
|
|
|
|
|
|
|
| Вычислительные навыки. |
|
|
|
|
|
|
|
|
|
|
27
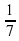
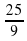
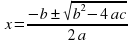
 Если знак неравенства то точки выколотые;
Если знак неравенства то точки выколотые;







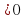
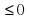


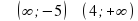
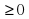
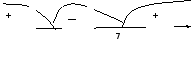
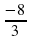
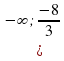 ]
]
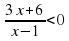 1) нули числителя: 3х+6 = 0, 3х= -6/:3, х= -2;
1) нули числителя: 3х+6 = 0, 3х= -6/:3, х= -2; 3)
3)