| 3 курс
| лекционный материал |
Лекция №10
Тема: Первообразная
План:
Определение первообразной
Основное свойство первообразной
Три правила нахождения первообразных
Определение первообразной
Вспомним пример из механики. Если в начальный момент времени 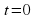 скорость тела равна 0, то есть
скорость тела равна 0, то есть 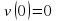 , то при свободном падении тело к моменту времени
, то при свободном падении тело к моменту времени 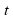 пройдет путь
пройдет путь
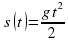
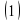
Формула 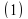 была найдена Галилеем экспериментально. Дифференцированием находим скорость:
была найдена Галилеем экспериментально. Дифференцированием находим скорость:
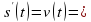
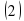
Второе дифференцирование дает ускорение:
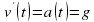
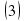
то есть ускорение постоянно.
Более типично для механики иное положение: известно ускорение точки 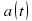 (в нашем случае оно постоянно), требуется найти закон изменения скорости
(в нашем случае оно постоянно), требуется найти закон изменения скорости 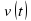 , а также найти координату
, а также найти координату 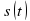 . Иными словами, по заданной производной
. Иными словами, по заданной производной 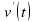 , равной
, равной 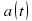 , надо найти
, надо найти 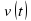 , а затем по производной
, а затем по производной 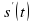 , равной
, равной 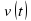 , найти
, найти 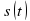 .
.
Для решения таких задач служит операция интегрирования, обратная операции дифференцирования.
Определение. Функция 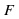 называется первообразной для функции
называется первообразной для функции 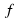 на заданном промежутке, если для всех
на заданном промежутке, если для всех 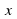 из этого промежутка выполняется равенство
из этого промежутка выполняется равенство
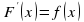
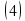
Пример 1. Функция 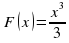 есть первообразная для функции
есть первообразная для функции 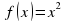 на интервале
на интервале 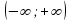 , так как
, так как
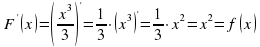
для всех 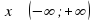 .
.
Легко заметить, что 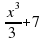 имеет ту же самую производную
имеет ту же самую производную 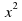 и поэтому также является первообразной для
и поэтому также является первообразной для 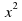 на
на 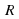 . Ясно, что вместо числа
. Ясно, что вместо числа 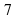 можно поставить любую постоянную. Таким образом, мы видим, что задача нахождения первообразной имеет бесконечно много решений. В следующем плановом вопросе мы увидим, как найти все эти решения.
можно поставить любую постоянную. Таким образом, мы видим, что задача нахождения первообразной имеет бесконечно много решений. В следующем плановом вопросе мы увидим, как найти все эти решения.
Пример 2. Для функции 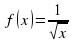 на интервале
на интервале 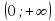 первообразной является функция
первообразной является функция
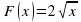 ,
,
так как
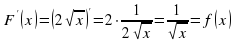
для всех 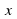 из этого интервала. Так же как и в примере 1, функция
из этого интервала. Так же как и в примере 1, функция 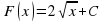 при любой постоянной
при любой постоянной 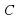 есть первообразная для функции
есть первообразная для функции 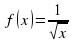 на том же интервале
на том же интервале 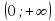 .
.
Пример 3. Функция 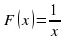 не является первообразной для функции
не является первообразной для функции 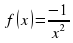 на промежутке
на промежутке 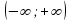 , так как равенство
, так как равенство 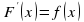 не выполнено в точке
не выполнено в точке 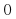 . Однако в каждом из промежутков
. Однако в каждом из промежутков 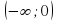 и
и 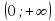 функция
функция 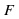 является первообразной для
является первообразной для 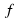 .
.
Основное свойство первообразной
Общий вид первообразных.
Задача интегрирования состоит в том, чтобы для заданной функции найти все ее первообразные. При решении этой задачи важную роль играет следующее утверждение:
Признак постоянства функции. Если  на некотором промежутке
на некотором промежутке  , то функция
, то функция 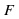 – постоянная на этом промежутке.
– постоянная на этом промежутке.
Доказательство. Зафиксируем некоторое  из промежутка
из промежутка  . Тогда для любого числа
. Тогда для любого числа 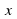 из такого промежутка в силу формулы Лагранжа можно указать такое число
из такого промежутка в силу формулы Лагранжа можно указать такое число  , заключенное между
, заключенное между 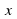 и
и  , что
, что
.
По условию  , так как
, так как  , следовательно,
, следовательно,
 .
.
Итак, для всех 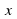 из промежутка
из промежутка 
 ,
,
то есть функция 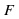 сохраняет постоянное значение.
сохраняет постоянное значение.
Все первообразные функции 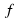 можно записать с помощью одной формулы, которую называют общим видом первообразных для функции
можно записать с помощью одной формулы, которую называют общим видом первообразных для функции 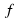 . Справедлива следующая теорема (основное свойство первообразных):
. Справедлива следующая теорема (основное свойство первообразных):
Теорема. Любая первообразная для функции 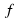 на промежутке
на промежутке  может быть записана в виде
может быть записана в виде

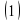
где – одна из первообразных для функции
– одна из первообразных для функции  на промежутке
на промежутке  , а
, а 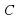 – произвольная постоянная.
– произвольная постоянная.
Поясним это утверждение, в котором кратко сформулированы два свойства первообразной:
1) какое бы число ни поставить в выражение 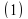 вместо
вместо 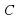 , получим первообразную для
, получим первообразную для 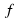 на промежутке
на промежутке  ;
;
2) какую бы первообразную  для
для 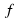 на промежутке
на промежутке  ни взять, можно подобрать такое число
ни взять, можно подобрать такое число 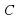 , что для всех
, что для всех 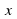 из промежутка
из промежутка  будет выполнено равенство
будет выполнено равенство
 .
.
Доказательство.
1) По условию функция 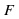
 первообразная для
первообразная для 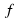 на промежутке
на промежутке  . Следовательно,
. Следовательно, 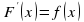 для любого
для любого  , поэтому
, поэтому
,
то есть – первообразная для функции
– первообразная для функции 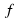 .
.
2) Пусть  – одна из первообразных для функции
– одна из первообразных для функции 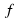 на том же промежутке
на том же промежутке  , то есть
, то есть

для всех  . Тогда
. Тогда
.
Отсюда следует в силу признака постоянства функции, что разность  есть функция, принимающая некоторое постоянное значение
есть функция, принимающая некоторое постоянное значение 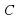 на промежутке
на промежутке  .
.
Таким образом, для всех 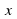 из промежутка
из промежутка  справедливо равенство
справедливо равенство  , что и требовалось доказать.
, что и требовалось доказать.
Основному свойству первообразной можно придать геометрический смысл: графики любых двух первообразных для функции 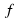 получаются друг из друга параллельным переносом вдоль оси
получаются друг из друга параллельным переносом вдоль оси  (рисунок 2.1,
(рисунок 2.1,  ).
).
Примеры нахождения первообразных.
Пример 1. Найдем общий вид первообразных для функции  на
на 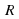 .
.
Заметим, что одной из первообразных функции 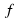 является функция
является функция  , так как
, так как  . В силу доказанной теоремы общий вид первообразных для функции
. В силу доказанной теоремы общий вид первообразных для функции 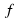 таков:
таков:
 .
.
Пример 2. Найдем первообразную  для функции
для функции  на промежутке
на промежутке 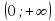 , принимающую при
, принимающую при  значение
значение  .
.
Легко проверить, что любая первообразная функции 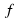 имеет вид
имеет вид  . Так как по условию
. Так как по условию  , приходим к уравнению (относительно
, приходим к уравнению (относительно 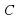 ) вида
) вида  , откуда
, откуда  , и, следовательно,
, и, следовательно,  .
.
Пример 3. Точка движется по прямой с постоянным ускорением  . В начальный момент
. В начальный момент  точка имеет начальную координату
точка имеет начальную координату  и начальную скорость
и начальную скорость  . Найдем координату
. Найдем координату  точки как функцию от времени.
точки как функцию от времени.
Так как  и
и  , из условия a
, из условия a получаем
получаем  . Отсюда следует, что
. Отсюда следует, что

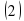
Подставляя  в формулу
в формулу  , находим
, находим  и
и
 .
.
Следовательно,
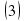
Чтобы найти  , подставим в
, подставим в  значение
значение  , откуда
, откуда  .
.
Итак,
.
Замечание. Для краткости при нахождении первообразной функции 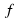 промежуток, на котором задана
промежуток, на котором задана 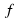 , обычно не указывают. Имеются в виду промежутки возможно большей длины. Так, в следующем примере естественно считать, что функция
, обычно не указывают. Имеются в виду промежутки возможно большей длины. Так, в следующем примере естественно считать, что функция 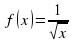 задана на интервале
задана на интервале 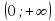 .
.
Пример 4. Найдем для функции 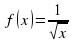 первообразную, график которой проходит через точку
первообразную, график которой проходит через точку  .
.
Любая первообразная функции 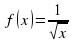 записывается в виде
записывается в виде  . Графики этих первообразных изображены на рисунке 2.1
. Графики этих первообразных изображены на рисунке 2.1  . Координаты точки
. Координаты точки  графика искомой первообразной должны удовлетворять уравнению
графика искомой первообразной должны удовлетворять уравнению  . Отсюда находим, что
. Отсюда находим, что  . Следовательно,
. Следовательно,
 .
.
Ниже приводится таблица первообразных для некоторых функций:
Проверьте правильность заполнения этой таблицы самостоятельно.
Примеры: Найти первообразную
 , тогда
, тогда 
 , тогда
, тогда
Три правила нахождения первообразных
Эти правила похожи на соответствующие правила дифференцирования.
Правило 1. Если 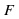 есть первообразная для
есть первообразная для 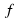 , a
, a  – первообразная для
– первообразная для  , то
, то  есть первообразная для
есть первообразная для  .
.
Действительно, так как  и
и  , по правилу вычисления производной суммы имеем:
, по правилу вычисления производной суммы имеем:
 .
.
Правило 2. Если 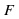 есть первообразная для
есть первообразная для 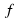 , a
, a  – постоянная, то функция
– постоянная, то функция  – первообразная для
– первообразная для  .
.
Действительно, постоянный множитель можно выносить за знак производной, поэтому
 .
.
Правило 3. Если  есть первообразная для
есть первообразная для  , a
, a  и
и  – постоянные, причем
– постоянные, причем  , то
, то  есть первообразная для
есть первообразная для  .
.
Действительно, по правилу вычисления производной сложной функции имеем:
.
Приведем примеры применения этих правил.
Пример 1. Найдем общий вид первообразных для функции
 .
.
Так как для  одна из первообразных есть
одна из первообразных есть  , а для
, а для  одной из первообразных является
одной из первообразных является  , по правилу 1 находим: одной из первообразных для функции
, по правилу 1 находим: одной из первообразных для функции  будет
будет  .
.
Ответ: .
Пример 2. Найдем одну из первообразных для функции  .
.
Так как для  одна из первообразных есть
одна из первообразных есть  , применяя правило 2, получаем ответ:
, применяя правило 2, получаем ответ:
 .
.
Пример 3. Найдем одну из первообразных для функции  .
.
Для  одной из первообразных является
одной из первообразных является  , поэтому по правилу 3 искомая первообразная равна .
, поэтому по правилу 3 искомая первообразная равна .
Пример 4. Найдем одну из первообразных для функции
.
Так как для  первообразной является
первообразной является  , по правилу 3 искомая первообразная равна
, по правилу 3 искомая первообразная равна
.
Пример 5. Материальная точка массой  килограмма движется по оси
килограмма движется по оси  под действием силы, направленной вдоль этой оси. В момент времени
под действием силы, направленной вдоль этой оси. В момент времени 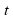 эта сила равна
эта сила равна  . Найдите закон
. Найдите закон  движения точки, если известно, что при
движения точки, если известно, что при  скорость точки равна
скорость точки равна  , а координата равна
, а координата равна  (
(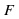 – сила в ньютонах,
– сила в ньютонах, 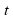 – время в секундах,
– время в секундах, 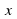 – путь в метрах).
– путь в метрах).
Согласно второму закону Ньютона  , где
, где 
 ускорение. Имеем
ускорение. Имеем
.
Скорость 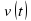 точки есть первообразная для ее ускорения
точки есть первообразная для ее ускорения 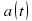 , поэтому
, поэтому
.
Постоянную  находим из условия
находим из условия  :
:
 ,
,
то есть

и
 .
.
Координата  есть первообразная для скорости
есть первообразная для скорости 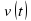 , поэтому
, поэтому
.
Постоянную  находим из условия
находим из условия  :
:
.
Итак, закон движения точки:
.
№ 345 (А. Н. Колмогоров, страница 178)
Найдите для функции 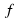 первообразную, график которой проходит через точку
первообразную, график которой проходит через точку  :
:


№ 1 1997 год 23
Укажите функцию  , если
, если  и
и  .
.
 .
.
Вопросы на закрепление темы
Дайте определение первообразной.
Определите основное свойство первообразной.
Чему равна первообразная для функции  ?
?
Чему равна первообразная для функции  ?
?
Чему равна первообразная для функции  ?
?
Чему равна первообразная для функции  ?
?
Чему равна первообразная для функции  ?
?
Чему равна первообразная для функции  ?
?
Определите три правила нахождения первообразных.
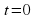 скорость тела равна 0, то есть
скорость тела равна 0, то есть 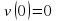 , то при свободном падении тело к моменту времени
, то при свободном падении тело к моменту времени 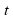 пройдет путь
пройдет путь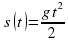
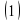
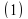 была найдена Галилеем экспериментально. Дифференцированием находим скорость:
была найдена Галилеем экспериментально. Дифференцированием находим скорость: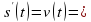
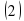
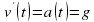
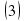
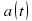 (в нашем случае оно постоянно), требуется найти закон изменения скорости
(в нашем случае оно постоянно), требуется найти закон изменения скорости 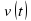 , а также найти координату
, а также найти координату 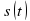 . Иными словами, по заданной производной
. Иными словами, по заданной производной 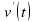 , равной
, равной 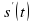 , равной
, равной 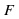 называется первообразной для функции
называется первообразной для функции 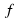 на заданном промежутке, если для всех
на заданном промежутке, если для всех 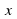 из этого промежутка выполняется равенство
из этого промежутка выполняется равенство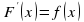
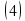
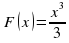 есть первообразная для функции
есть первообразная для функции 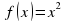 на интервале
на интервале 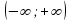 , так как
, так как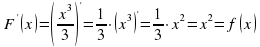
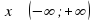 .
.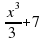 имеет ту же самую производную
имеет ту же самую производную 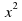 и поэтому также является первообразной для
и поэтому также является первообразной для 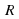 . Ясно, что вместо числа
. Ясно, что вместо числа 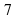 можно поставить любую постоянную. Таким образом, мы видим, что задача нахождения первообразной имеет бесконечно много решений. В следующем плановом вопросе мы увидим, как найти все эти решения.
можно поставить любую постоянную. Таким образом, мы видим, что задача нахождения первообразной имеет бесконечно много решений. В следующем плановом вопросе мы увидим, как найти все эти решения.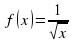 на интервале
на интервале 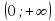 первообразной является функция
первообразной является функция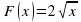 ,
, 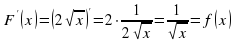
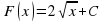 при любой постоянной
при любой постоянной 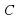 есть первообразная для функции
есть первообразная для функции 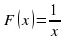 не является первообразной для функции
не является первообразной для функции 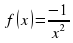 на промежутке
на промежутке 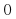 . Однако в каждом из промежутков
. Однако в каждом из промежутков 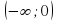 и
и 















