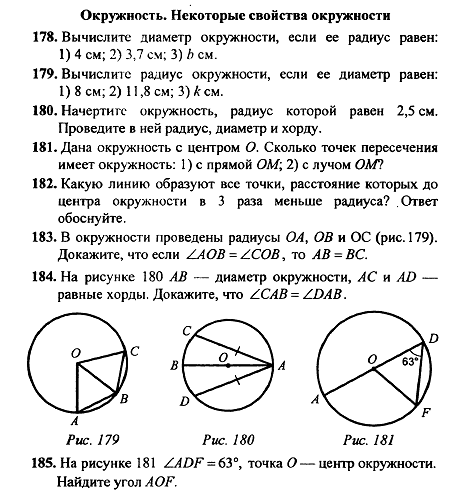
| Открываем тетради, записываем число, сегодня 19 февраля. Тема урока: «Окружность и ее элементы» Понятие окружности и ее элементов является для вас не новым. Вы с ним уже знакомились в математики 5-6 класса.
Какие элементы окружности вы знаете? У окружности еще есть такие элементы как хорда, дуга окружности.
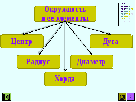
Давайте запишем определение окружности. Определение 1. Окружностью называется геометрическая фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Точка О – называется центром окружности. Какой следующий элемент окружности? Определение 2. Любой отрезок, соединяющий точку окружности с ее центром, называется радиусом. Радиусом данной окружности будет отрезок 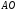 . . Окружность обозначают Обозначают буквой 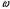 – омега. – омега. 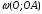 эта запись читается так: окружность с центром в точке эта запись читается так: окружность с центром в точке 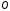 и радиусом и радиусом 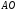 . . Что вы можете сказать про радиусы одной и той же окружности? Учитель наглядно показывает используя программу Живая геометрия, что все радиусы одно и той же окружности равны.
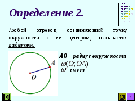
Какой у нас следующий элемент окружности? Определение 3. Отрезок, соединяющий две точки окружности, называется хордой. На данной окружности 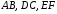 – хорды. – хорды.
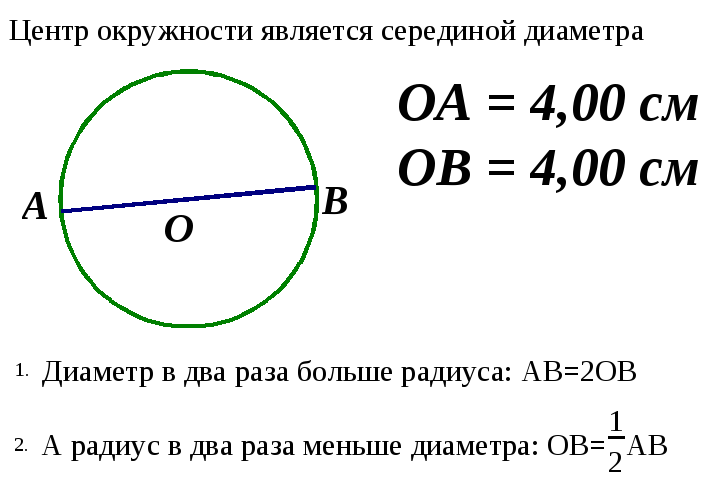
Какой у нас следующий элемент окружности? Определение 4. Хорда, проходящая через центр окружности, называется диаметром. На данной окружности  – диаметр. – диаметр.
Центр окружности является серединой диаметра. Как вы думаете как взаимосвязаны диаметр и радиус? Диаметр в два раза больше радиуса:  А радиус в два раза меньше диаметра: 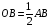 . . Учитель с помощью Живой геометрии наглядно показывает этот факт. Давайте закрепим все, что мы сейчас изучили. Назовите мне окружность. Назовите центр окружности. Назовите радиусы окружности. Назовите хорды окружности. Назовите диаметр окружности. Какой у нас следующий элемент окружности? Определение 5 Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. На данной окружности дуги 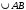 и и  . . Как вы понимаете полуокружность? Дуга называется полуокружностью, если отрезок, соединяющий ее концы является диаметром. 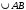 – полуокружность. – полуокружность.
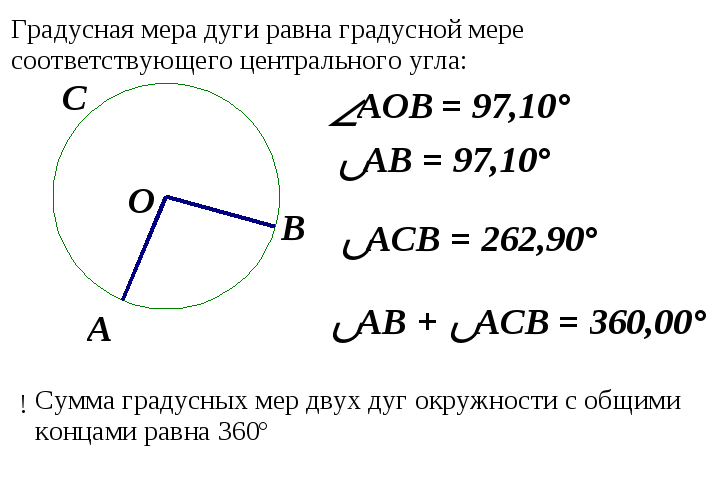
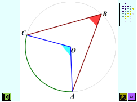
Сегодня мы еще познакомимся с центральным и вписанным углом Определение 6. Угол, с вершиной в центре окружности называется центральным углом. Градусная мера дуги равна градусной мере соответствующего центрального угла: На данном чертеже  – центральный угол – центральный угол
Учитель наглядно показывает этот факт, используя живую геометрию (Чертеж 4) Чему равна градусная мера полуокружности?
Если градусная мера полуокружности равна  , то чему равна градусная мера всей окружности? , то чему равна градусная мера всей окружности? Сумма градусных мер двух дуг окружности с общими концами равна 360°.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называют вписанным углом. На данной окружности  – вписанный угол – вписанный угол Учитель показывает какие бывают списанные углы с помощью живой геометрии
Вписанный угол измеряется половиной дуги, на которую он опирается. Эту теорему мы докажем на следующем уроке.
Учитель показывает эту теорему наглядно (Чертеж 6)
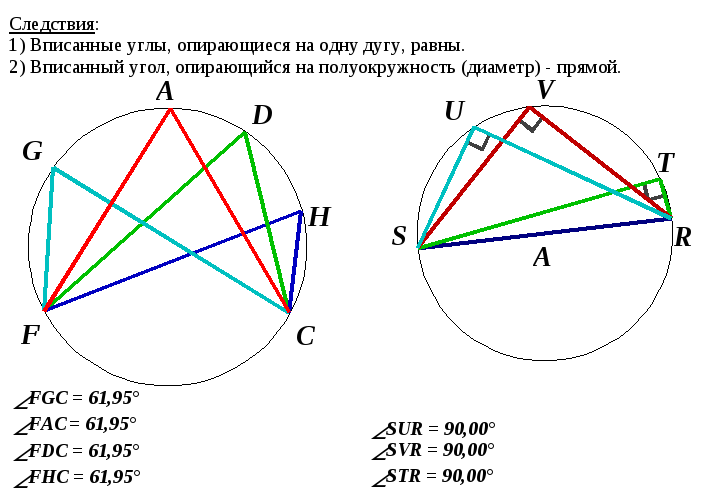
Запишем еще 2 следствие из этой теоремы (чертеж 7) Следствия: 1) Вписанные углы, опирающиеся на одну дугу, равны. 2) Вписанный угол, опирающийся на полуокружность (диаметр) - прямой. Давайте закрепим понятия центральный и вписаны угол. (Слайд 12) – Назовите центральный угол. – Чему равна его градусная мера? – Назовите вписанный угол. – Чему равна его градусная мера?
Сегодня еще вспомним что такое круг. Какую фигуру называют кругом? Давайте запишем точное определение круга. Определение 8. Часть плоскости, ограниченная окружностью, называется кругом. – Чему равна площадь круга? – Чему равно число 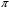 ? ?
| 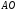 .
. 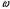 – омега.
– омега. 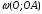 эта запись читается так: окружность с центром в точке
эта запись читается так: окружность с центром в точке 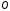 и радиусом
и радиусом 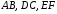 – хорды.
– хорды. – диаметр.
– диаметр.
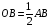 .
.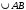 и
и  .
. – центральный угол
– центральный угол , то чему равна градусная мера всей окружности?
, то чему равна градусная мера всей окружности?  – вписанный угол
– вписанный угол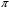 ?
?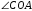 – центральный угол
– центральный угол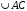
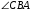 – центральны угол
– центральны угол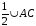
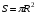










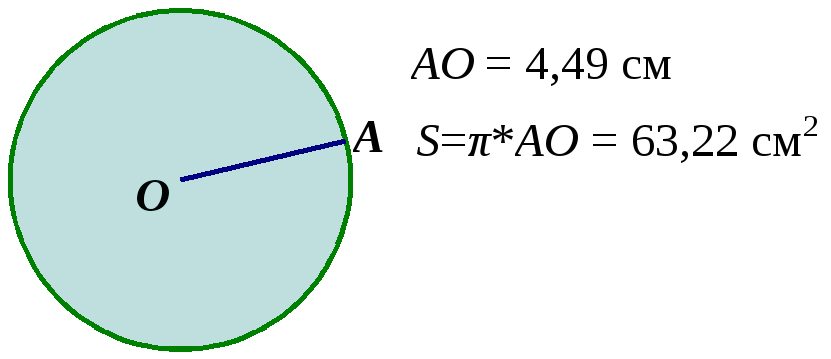
 – радиус.
– радиус.