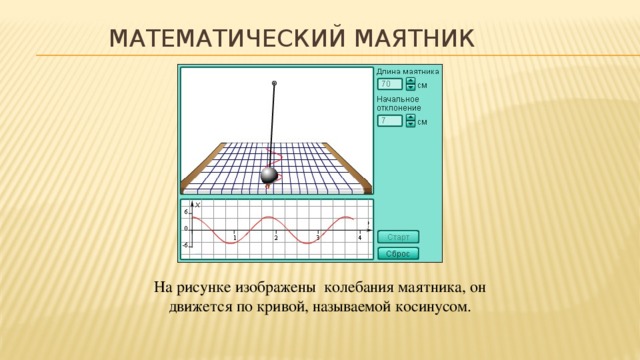
Цель урока - рассмотреть общие подходы решения тригонометрических уравнений, закрепить навыки и проверить умение решать тригонометрические уравнения, кроме того, познакомиться с новыми способами решения некоторых известных тригонометрических уравнений, историей тригонометрии, а также использованием тригонометрии в повседневной жизни.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Ох уж, эта тригонометрия!
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Ох уж, эта тригонометрия! »
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1690 руб.
2820 руб.
1720 руб.
2860 руб.
1430 руб.
2380 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства





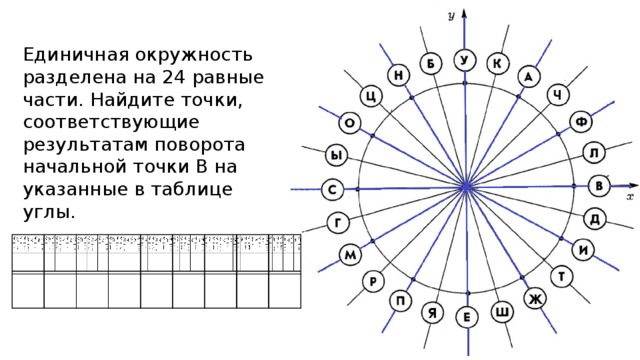
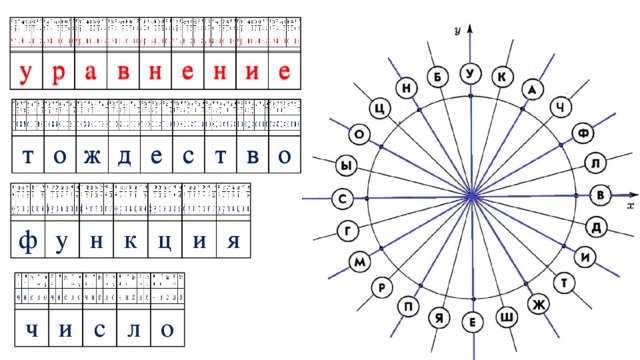


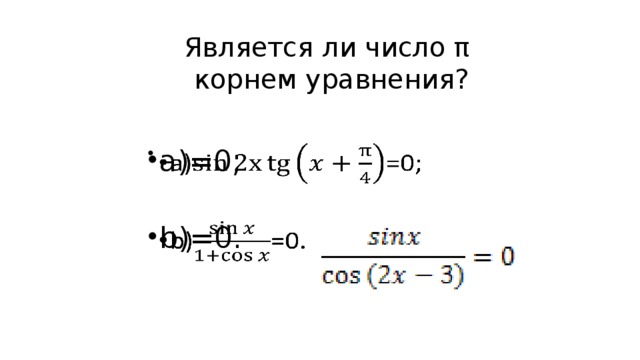

![Решите уравнение соs2x=sin(x+π/2). б) Найдите корни этого уравнения, принадлежащие промежутку [-2π; -π]](https://fsd.kopilkaurokov.ru/uploads/user_file_5554ae4de8014/img_user_file_5554ae4de8014_12.jpg)