Обоснование актуальности проекта.
Тригонометрия - это раздел математики, изучающий тригонометрические функции. Сложно представить, но с этой наукой мы сталкиваемся не только на уроках математики, но и в нашей повседневной жизни. Вы могли не подозревать об этом, но тригонометрия встречается в таких науках, как физика, биология, не последнюю роль она играет и в медицине, и, что самое интересное, без нее не обошлось даже в музыке и архитектуре.
Слово тригонометрия впервые появляется в 1505 году в заглавии книги немецкого математика Питискуса.
Тригонометрия – слово греческое, и в буквальном переводе означает измерение треугольников ( trigonan – треугольник, metreo - измеряю).
Возникновение тригонометрии было тесно связано с землемерием, астрономией и строительным делом.…
Школьник в 14-15 лет не всегда знает, куда пойдет учиться и где будет работать.
Для некоторых профессий ее знание необходимо, т.к. позволяет измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Принципы тригонометрии, используются и в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
- Определение предмета исследования
Почему знания тригонометрии необходимы для современного человека?
3. Цели проекта.
Связь тригонометрии с реальной жизнью.
- Проблемный вопрос
1. Какие понятия тригонометрии чаще всего используются в реальной жизни?
2. Какую роль играет тригонометрия в астрономии, физике, биологии и медицине?
3. Как связаны архитектура, музыка и тригонометрия? - Гипотеза
Большинство физических явлений природы, физиологический процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.
- Проверка гипотезы
Тригонометрия (от греч. trigonon – треугольник, metro – метрия) – микрораздел математики , в котором изучаются зависимости между величинами углов и длинами сторон треугольников, а также алгебраические тождества тригонометрических функций.
Зачатки тригонометрических познаний зародились в древности. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вспомогательным разделом.
История тригонометрии:
Истоки тригонометрии берут начало в древнем Египте, Вавилонии и долине Инда более 3000 лет назад.
Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом и Птолемеем.
Древние люди вычисляли высоту дерева, сравнивая длину его тени с длиной тени от шеста, высота которого была известна. По звездам вычисляли местонахождение корабля в море.
Следующий шаг в развитии тригонометрии был сделан индийцами в период с V по XII в.
Сам термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в.из так называемого «синуса дополнения», т.е. синуса угла, дополняющего данный угол до 90°. «Синус дополнения» или ( по латыни) sinus complementi стали сокращенно записывать как sinus co или co-sinus.
В XVII – XIX вв. тригонометрия становится одной из глав математического анализа.
Она находит большое применение в механике, физике и технике, особенно при изучении колебательных движений и других периодических процессов.
Жан Фурье доказал, что всякое периодическое движение может быть представлено (с любой степенью точности) в виде суммы простых гармонических колебаний.
Стадии развития тригонометрии:
- Тригонометрия была вызвана к жизни необходимостью производить измерения углов.
- Первыми шагами тригонометрии было установление связей между величиной угла и отношением специально построенных отрезков прямых. Результат - возможность решать плоские треугольники.
- Необходимость табулировать значения вводимых тригонометрических функций.
- Тригонометрические функции превращались в самостоятельные объекты исследований.
- В XVIII в. тригонометрические функции были включены
в систему математического анализа.
Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.
Тригонометрия в астрономии:
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)
Достижения Виета в тригонометрии
Полное решение задачи об определении всех элементов плоского или сферического треугольников по трем данным элементам, важные разложения sin пх и cos пх по степеням cos х и sinx. Знание формулы синусов и косинусов кратных дуг дало возможность Виету решить уравнение 45-й степени, предложенное математиком А. Рооменом; Виет показал, что решение этого уравнения сводится к разделению угла на 45 равных частей и что существуют 23 положительных корня этого уравнения. Виет решил задачу Аполлония с помощью линейки и циркуля.
Решение сферических треугольников- одна из задач астрономии Вычислять стороны и углы любого сферического треугольника по трем подходящим образом заданным сторонам или углам позволяют следующие теоремы: (теорема синусов) (теорема косинусов для углов) (теорема косинусов для сторон).
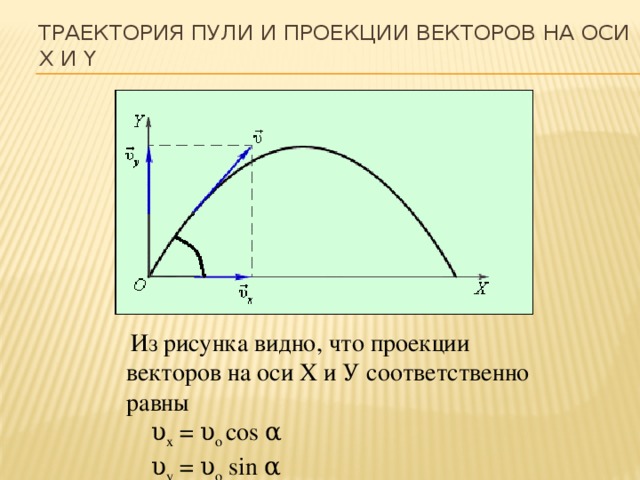
Тригонометрия в физике:
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.
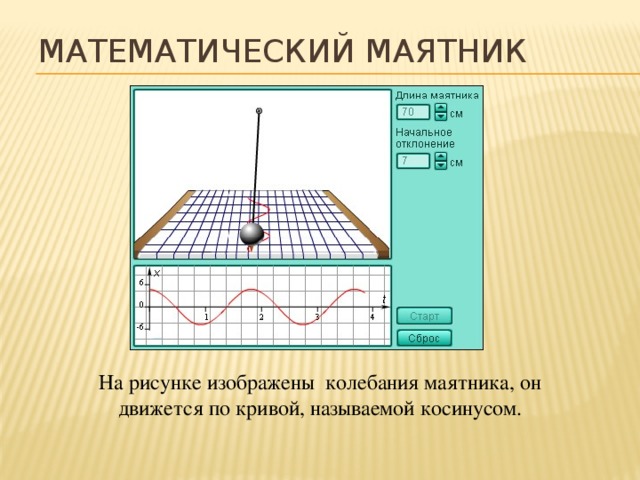
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, r — начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде x’’ + ω²x = 0.
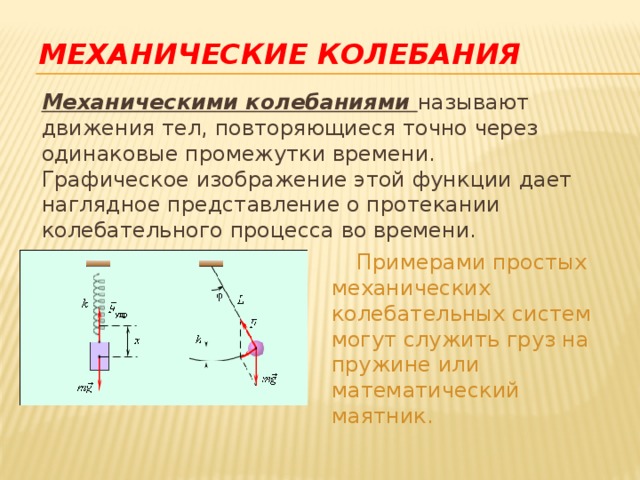
Механические колебания . Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.
Тригонометрия в природе.
Мы часто задаем вопрос «Почему мы иногда видим то, чего нет на самом деле?». Для исследования предложены следующие вопросы: «Как возникает радуга? Северное сияние?», «Что такое оптические иллюзии?» ,«Как тригонометрия может помочь найти ответы на эти вопросы?».
Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.
Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
Многофункциональная тригонометрия
- Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
- К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
- Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Тригонометрия и тригонометрические функции в медицине и биологии.
- Одно из фундаментальных свойств живой природы - это цикличность большинства происходящих в ней процессов.
- Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
- Основной земной ритм – суточный.
- Модель биоритмов можно построить с помощью тригонометрических функций.
Тригонометрия в биологии
Какие биологические процессы связаны с тригонометрией?
- Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
- Биологические ритмы, биоритмы связаны с тригонометрией
Связь биоритмов с тригонометрией
- Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Возникновение музыкальной гармонии
- Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.
- Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
- диатоническая гамма 2:3:5
Тригонометрия в архитектуре
- Детская школа Гауди в Барселоне
- Страховая корпорация Swiss Re в Лондоне
- Феликс Кандела Ресторан в Лос-Манантиалесе
- Интерпретация
Мы привели лишь малую часть того, где можно встретить тригонометрические функции.. Мы выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
Мы доказали, что тригонометрия тесно связана с физикой, встречается в природе, медицине. Можно приводить бесконечно много примеров периодических процессов живой и неживой природы. Все периодические процессы можно описать с помощью тригонометрических функций и изобразить на графиках
Мы думаем, что тригонометрия нашла отражение в нашей жизни, и сферы,
в которых она играет важную роль, будут расширяться.
Заключение
- Выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
- Доказали, что тригонометрия тесно связана с физикой, встречается в природе, музыке, астрономии и медицине.
- Думаем, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.

































![Феликс Кандела Ресторан в Лос-Манантиалесе [a d cos(t) + d d t , b d sin(t), c d t + e d t 2 ]](https://fsd.kopilkaurokov.ru/uploads/user_file_543377869d43e/img_user_file_543377869d43e_1_37.jpg)



















