"Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции"

Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции

Ревенко А.А.

Методы решения уравнений и неравенств, содержащих обратные тригонометрические функции, опираются на их свойства, а также на формулы, их связывающие. Свойства ограниченности и монотонности являются ключевыми при решении уравнений и неравенств с обратными тригонометрическими функциями. В данной статье рассматривается 4 основных метода решения таких уравнений и неравенств, приводятся образцы этих заданий.

1. Уравнения и неравенства, левая и правая части которых являются одноименными обратными тригонометрическими функциями. Данный метод основывается на свойстве монотонности этих функций. Примером могут служить следующие уравнения и неравенства.

Пример. Решить уравнение

Решение. Уравнение равносильно системе

Ответ:.

Пример. Решить неравенство

Решение. Приведем неравенство к переходу 1 б). Для этого вспомним формулу

Ответ: [-

1. Уравнения и неравенства, левая и правая части которых являются разноименными обратными тригонометрическими функциями.

При решении уравнений и неравенств, левая и правая части которых являются разноименными обратными тригонометрическими функциями, пользуются известными тригонометрическими тождествами.

Пример. Решить неравенство

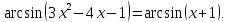
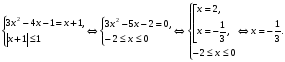
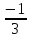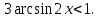
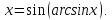
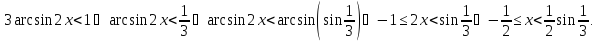
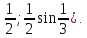
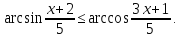
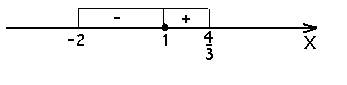
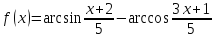Решение. Рассмотрим функцию и решим неравенство 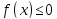методом интервалов.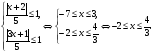

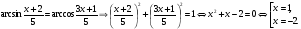
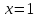1. Найдем D(f). Для этого решим систему

2. Найдем нули функции f(x) . Для этого решим уравнение

Проверка.

получим 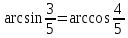- верно

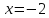получим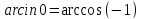 неверно, следовательно, х=-2 является посторонним корнем.

3. Решим неравенство методом интервалов.

Рис.1

Ответ:[-2;1].

1. Метод замены переменной.

Некоторые уравнения и неравенства, которые содержат обратные тригонометрические функции, можно сводить к алгебраическим, для этого необходимо сделать соответствующую замену переменной.

Пример. Решите уравнение

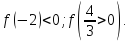
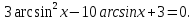
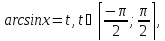Решение. Обозначим получим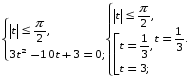

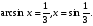
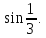
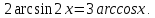
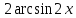Вернемся к переменной х.

Ответ:

1. Использование свойств монотонности и ограниченности обратных тригонометрических функций.

Решения некоторых уравнений неравенств, которые содержат обратные тригонометрические функции, основываются на определенных свойствах этих функций.

Пример. Решить уравнение

Решение. Функция y= является монотонно возрастающей, а функция y= 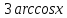- монотонно убывающей, следовательно, уравнение имеет не более одного корня. Методом подбора найдем корень уравнения. Число х = 0,5 является корнем этого уравнения.

Ответ: 0,5.

В данной работе мы рассмотрели свойства обратных тригонометрических функций и составили классификацию методов решения уравнений и неравенств, содержащих аркфункции. Статья содержит не только теоретический материал, но и практический (к каждому методу приводится пример с решением).Этот материал может быть полезен учителям, работающим в общеобразовательных и математических классах, а так же ученикам, поступающим в ВУЗы.

БИБЛИОГРАФИЯ

1. Карп А.П. Сборник задач по алгебре и началам анализа: учебное пособие для учащихся шк. и классов с углубл. изуч. математики. – М.: Просвещение, 1995.

2. Мирошин, В.В. Обратные тригонометрические функции [Текст] / В.В. Мирошин. – М.: Чистые пруды, 2007– 32 с.

3. Фалин, Г.И. Обратные тригонометрические функции. 10-11 классы — М.: Издательство «Экзамен», 2012. — 221с.