Учитель математики высшей квалификационной категории
Ужачкина Надежда Павловна.
Урок №3 по теме «Модуль действительного числа».
Цели:
повторить понятие модуля, его свойства, геометрический смысл модуля, правила построения графика функции у = |х| и случаи примениния графического способа решения; проверить умение обучающихся применять определение модуля при упрощении выражений и решении уравнений, содержащих модули; проверить умение обучающихся строить график функции у = |х| и решать графическим способом уравнения, системы уравнений, неравенства, содержащие модуль;
развивать речевую культуру обучающихся; продолжать развивать умение систематизировать полученные знания, описывать ситуацию математическим языком, переводить математический язык на обыкновенный; развивать навыки самоконтроля и взаимоконтроля, учиться оценивать результаты выполненных действий;
воспитывать организованность, дисциплинированность, самостоятельность, внимательность, воспитание мотивов добросовестного отношения к труду.
1. Организационный момент.
Приветствие, оформление тетрадей, урока (привлечь учеников к постановке цели урока), повторение правил к уроку (работа в парах).
2. Актуализация знаний.
1. Что называют модулем действительного числа?
2. Как упростить выражение 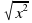 ?
?
3. Какими свойствами обладает модуль?
4. При выполнении каких заданий можно применять свойства модуля?
5. В чем заключается геометрический смысл модуля?
6. Как найти расстояние между точками А(а) и В(в) на числовой прямой?
7. Сколько корней может иметь уравнение вида |х| = а?
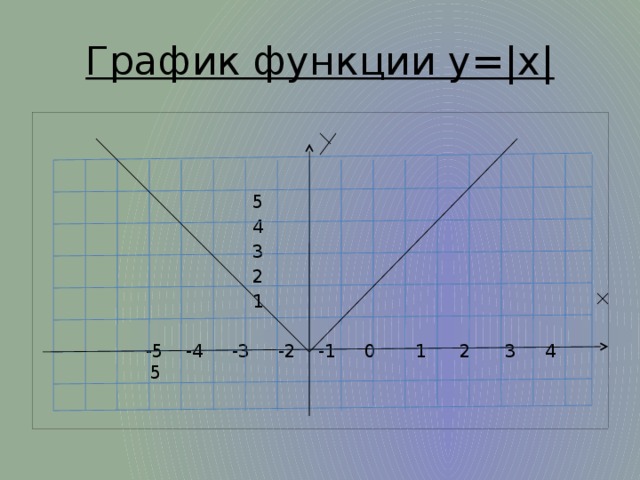
8. Какого вида функция у = |х|?
9. Какая линия является графиком этой функции?
10. При выполнении каких заданий применяют построение графиков?
3. Самостоятельная работа.
Давайте проверим, как на прошлых уроках и дома вы научились упрощать выражения, содержащие модуль.
Выполняем задание 1) из карточек. На эту работу отводится 4 минуты.
Самостоятельная работа по теме «Модуль действительного числа».
Вариант 1.
1) Найдите значение выражения:
а) |-5|; б) |7,2|; в) |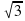 |- 2; г)
|- 2; г) 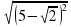 ; д)
; д) 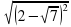 -
- 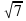 + 4.
+ 4.
2) Решите уравнение: а) |х| = 3; б) |х + 2| = 4; в) |х - 7| = 0;
г) |4х + 1| = 5; д) 2|х| + |- х| = 15.
3) Постройте графики функций у = |х| и у = 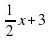 .
.
С помощью графиков решите : а) уравнение |х| = 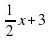 ;
;
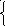 б) систему уравнений у = |х|,
б) систему уравнений у = |х|,
у = 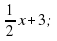
в) неравенство |х| ≥ 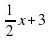 ;
;
г) неравенство |х| 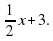
Самостоятельная работа по теме «Модуль действительного числа».
Вариант 2.
1) Найдите значение выражения:
а) |5|; б) |-7,2|; в) |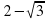 |; г)
|; г) 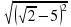 ; д)
; д) 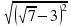 +
+ 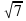 - 1.
- 1.
2) Решите уравнение: а) |х| = 4; б) |х - 2| = 3; в) |х + 7| = -1;
г) |2х + 2| = 6; д) 3|х| - |- х| = 16.
3) Постройте графики функций у = |х| и у = - 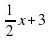 .
.
С помощью графиков решите : а) уравнение |х| = - 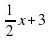 ;
;
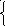 б) систему уравнений у = |х|,
б) систему уравнений у = |х|,
у = - 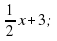
в) неравенство |х| ≤ - 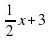 ;
;
г) неравенство |х| - 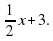
Поменяйтесь работами с соседом по парте, оцените работу и поставьте оценку за этот этап работы. Готовые ответы смотрите на экране.
Верно выполнены все 5 случаев – «5»,
4 – «4»,
3 – «3»,
2-1 – «2».
Ответы: а) 5; б) 7,2; в) 2 - 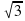 ; г) 5 -
; г) 5 - 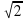 ; д) 2.
; д) 2.
4. Самостоятельная работа.
Проверим, как научились решать простейшие уравнения с модулем. Выполняем задание 2), для этой работы у вас есть 7 минут.
Поменяйтесь тетрадями с соседом позади себя, проверьте получившиеся корни уравнений по готовым ответам на экране. Оцените работу.
Верно выполнены все 5 случаев – «5»,
4 – «4»,
3 – «3»,
2-1 – «2».
Ответы:
Вариант 1. Вариант 2.
а) – 3; 3; а) – 4; 4;
б) – 6; 2; б) – 1; 5;
в) 7; в) корней нет;
г) – 1,5; 1; г) – 4; 2;
д) – 5; 5; д) – 8; 8.
5. Только ли в математике мы встречаемся с понятием модуля?
Посмотрите, что еще означает этот термин в других сферах деятельности.
- Модуль упругости (в физике) – величина, характеризующая упругие свойства твердых тел, коэффициент деформации.
- Модуль (в архитектуре и строительстве) – исходная мера, принятая для выражения кратных соотношений размеров комплексов, сооружений и их частей.
- Модуль (в радиоэлектронике) – унифицированный функциональный узел радиоэлектронной аппаратуры, выполненный в виде самостоятельного изделия.
- Модуль зубчатого колеса (в технике) – геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса.
6. Самостоятельная работа.
Осталось проверить умение строить графики и умения решать графически уравнения, системы уравнений, неравенства. На обороте доски работают два человека по вариантам, остальные в тетрадях. Выполняем задание 3), для этого у вас 10 минут.
Поменяйтесь тетрадями с соседом впереди себя, проверьте построение графиков и ответы на поставленные вопросы, оцените работу.
Если все верно, то заработана оценка «5»,
допущена одна ошибка – «4»,
допущены две ошибки – «3»,
допущены три ошибки при ответах – «2»,
неверно построены графики – «1».
7. Итоги урока, домашнее задание.
Подсчитайте среднее арифметическое трех оценок. Это ваша предварительная оценка за самостоятельную работу сегодня.
- Кто получил «5»? «4»? «3»? «2»?
- Довольны ли вы своей оценкой?
- Те, кто желает улучшить результат, или чувствует, что недостаточно хорошо отработал навыки, выполняют следующие задания.
Уровень «3 – 4»: №16.1 – 4 вг, 16.27 вг, 16.13, 16.38 б, 16.21 – 24 б.
Уровень «4 – 5»: №16.33 вг, 16.27 вг, 16.41 бг, 16.38 б, 16.29 – 30 аб.
На дополнительную оценку: 16.36, 16.42.
- Какие вопросы у вас возникли при выполнении самостоятельной работы?
- Просмотрите домашнее задание. Все ли понятно?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 - 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| - 5; б) |х| - 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 - 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| - 5; б) |х| - 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 - 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| - 5; б) |х| - 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 - 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| - 5; б) |х| - 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 - 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| - 5; б) |х| - 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 - 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| - 5; б) |х| - 5?
Дополнительные задания для самостоятельной работы.
Решите уравнение: а) х2 - 4|х| = 0; б) а) х2 + 4|х| = 0.
Сколько решений имеет неравенство: а) |х| - 5; б) |х| - 5?
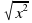 ?
? 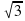 |- 2; г)
|- 2; г) 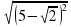 ; д)
; д) 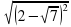 -
- 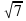 + 4.
+ 4.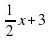 .
.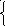 б) систему уравнений у = |х|,
б) систему уравнений у = |х|,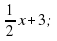
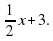
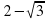 |; г)
|; г) 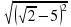 ; д)
; д) 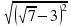 +
+ 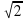 ; д) 2.
; д) 2.



 0, то х 1 = а; х 2 = - а 2) Если а = 0, то х = 0 3) Если а" width="640"
0, то х 1 = а; х 2 = - а 2) Если а = 0, то х = 0 3) Если а" width="640"


 0, то х 1 = а; х 2 = - а 2) Если а = 0, то х = 0 3) Если а" width="640"
0, то х 1 = а; х 2 = - а 2) Если а = 0, то х = 0 3) Если а" width="640"


![Ответы к заданию 3 Вариант 1. Вариант 2. а) - 2;6; а) – 6; 2; б) ( - 2; 2), (6; 6); б) ( - 6; 6), (2; 2); в) (- ∞; -2]U[6; + ∞); в) [-6;2]; г) ( – 2; 6); г) (- ∞; -6)U(2; + ∞) Если все верно, то заработана оценка «5», допущена одна ошибка – «4», допущены две ошибки – «3», допущены три ошибки – «2», неверно построены графики – «1».](https://fsd.kopilkaurokov.ru/uploads/user_file_57ed4deeeb758/img_user_file_57ed4deeeb758_1_11.jpg)

















