Современные ученики должны иметь глубокие знания по широкому кругу вопросов и уметь результативно применять эти знания, делать выводы и обосновывать результаты собственных исследований. Для этого необходима глубокая математическая подготовка и хорошая мотивация к изучению предмета.В классе с углубленным изучением математики наиболее полно можно осуществить переход от учения как функции запоминания к учению как процессу умственного развития, позволяющему использовать усвоенное. Задания, используемые на данном уроке входят во вторую часть ОГЭ и позволяют учащимся в полной мере овладеть приемами решения уравнений с модулями.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок в 9 классе с углублённым изучением математики по теме: Модуль действительного числа. Решение уравнений и неравенств с модулем
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«konspekt5»
Просмотр содержимого презентации
«21_L8v»
Просмотр содержимого презентации
«21_L8v»
Полезное для учителя
Распродажа видеоуроков!
2220 руб.
3170 руб.
2020 руб.
2880 руб.
2000 руб.
2860 руб.
1570 руб.
2240 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства










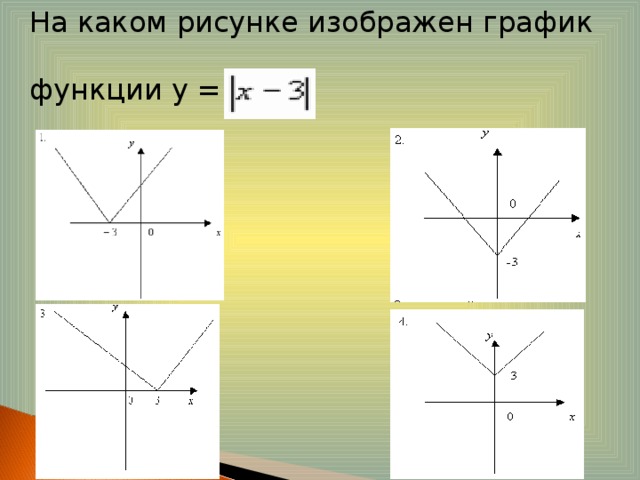



 3 , то /а / 3 2) если a 4 , то /а / 4 3) если a -2 , то /а / 2 4) если -5 5 5) если a - 3, то /а / 3" width="640"
3 , то /а / 3 2) если a 4 , то /а / 4 3) если a -2 , то /а / 2 4) если -5 5 5) если a - 3, то /а / 3" width="640"



 1" width="640"
1" width="640"






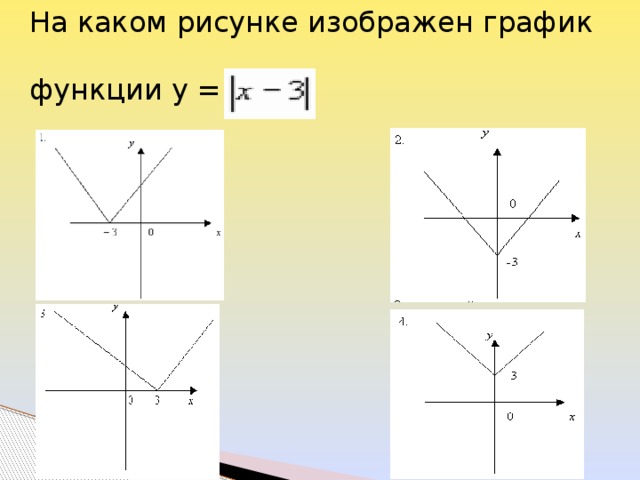


 3, то /а / 3 2) если a 4, то /а / 4 3)если a -2, то /а / 2 4) если -5 5 5) если a -3, то /а / 3" width="640"
3, то /а / 3 2) если a 4, то /а / 4 3)если a -2, то /а / 2 4) если -5 5 5) если a -3, то /а / 3" width="640"



 1" width="640"
1" width="640"
















