Урок по теме «Решение тригонометрических уравнений»
М. В. Ледрова (ГБОУ СПО НО «НМБК»)
ТИП УРОКА: изучение нового материала
ЦЕЛИ УРОКА:
Образовательная: образовать понятие однородных тригонометрических уравнений, сформировать у студентов умение решать однородные тригонометрические, отработать навыки решения всех видов изученных ранее тригонометрических уравнений.
Развивающая: развивать и совершенствовать умения применять имеющиеся у студентов знания в измененной ситуации, развивать логическое мышление, умение делать выводы и обобщения.
Воспитательная: воспитывать у студентов аккуратность, культуру поведения, чувство ответственности, стремление к расширению кругозора.
Урок проводится в форме игры. Группа делится на 3 команды-по рядам.
Содержание урока
1.Организационный этап
Взаимное приветствие, проверка подготовленности учащихся к уроку.
2.Этап актуализации опорных знаний.
Конкурс «Проверка быстроты реакции» (устный диктант по формулам и основным понятиям)
Вопросы:
- Что называется арксинусом числа а?
- Чему равен arcsin(-a)?
- Назовите формулу для нахождения корней уравнения вида sin x=a
- Что называется арккосинусом числа а?
- Чему равен arccos(-a)
- Назовите формулу для нахождения корней уравнения вида cos х = а
- Всегда ли уравнения вида sin х = а и
- x = а имеют корни?
- Что называется арктангенсом числа а?
- Чему равен арктангенс (-а)?
- Назовите формулу для нахождения корней уравнения tg x=a
- Каким должно быть число а, чтобы уравнение tg x=a и ctg x = а имело корни?
- Верно ли, что: 1) arcsin 1=П/2
2) arcsin (-1)=3П/2
3) arccos1=2П
Конкурс «Ложные показания»
Сейчас от каждой команды к доске выйдут по 1 представителю и решат по 1 уравнению из домашней работы, намеренно делая ошибки в ходе решения:
1.sin x/2 + 1=0
2.3 cos ^2 x- sin x - 1 = 0
3. 2 cos (п/3 + 3x) -1 =0
Во время подготовки студентов у доски с командами проводится конкурс на умение вести «Перекрестный допрос»
Дополнительное задание для команд. На слайде записаны уравнения:
1. 2sinx*cosx=1
2. cos^2 x - sin ^2 x = 1
3. ctg x =1
Проверка работы, выполненной на доске
Студенты поднимают руки и дают ответы.
За каждый правильный ответ команда получает жетон
Трое студентов из разных команд выходят к доске по вызову и решают уравнения, делая в решении по несколько ошибок
Один студент из каждой команды выбирается в качестве свидетеля. Команды противников решают простейшие тригонометрические уравнения, свидетель должен назвать корни этих уравнений (по 2-3 вопроса от каждой команды)
Студенты устно решают эти уравнения
Студенты команд противников ищут ошибки, допущенные в решении, и предлагают правильное решение
3. этап подготовки к усвоению нового материала и усвоение нового материала. Конкурс «Умение проводить экспертизу»
На доске записаны тригонометрические уравнения.
Студенты называют те уравнения, способ решения которых вы знаете
1) sin ( 4x-2 ) =1/2
2) 2sinx-3cosx=0
3) cos ^ 2 x - sin ^2 x =-1
4) 3 sin ^2 x - 4sinx cosx +cos^2x=0
В результате проделанной работы на доске остались уравнения, которые студенты затрудняются решить.
- На доске оставались уравнения, которые называются однородными тригонометрическими уравнениями относительно синуса и косинуса.
- Запишите тему урока «Однородные тригонометрические уравнения».
- Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным.
- Какую степень имеют слагаемые в уравнении
- Какое уравнение называется однородным уравнением первой степени?
- Какую степень имеют слагаемые в уравнении
- Это однородное уравнение второй степени.
- Рассмотрим способы решения таких уравнений
Доска и лист делятся на две одинаковые колонки
Однородные уравнения 1-ой степени
Примеры
asinx+bcosx=0 |:cosx<>0, a<>0, b<>0
atgx+b=0
Студенты называют уравнения и говорят, как его решать. После сказанного, если нет замечаний, слайд с записью названного уравнения убирается с экрана.
Студенты записывают дату, тему и определение однородного уравнения.
В ходе беседы студенты отвечают на вопросы
Студенты выполняют записи в тетради, в ходе объяснения задают вопросы.
4.Этап проверки понимания студентами нового материала и его закрепление.
Конкурс «Умение применять результат».
- Определите вид уравнения и укажите способ его решения:
- sin x + cos x =0
- Sin x = 2cos x
- 4cos 3x – 5sin3x = 0
- Sin2x -5 sin x cos x +6 cos2x = 0
- 1 - 4 sin x cos x + 2 cos2x = 0
- 4 Sin2 2x + 3 sin 4x + 2 cos2 2x = 0
Самостоятельная работа обучающего характера.
1 команда выполняет b,c
2 команда выполняет e
3 команда выполняет f
Студенты поднимают руку, называют вид уравнения и объясняют, как его можно решить.
Студенты решают уравнения в тетрадях. Первый выполнивший задание воспроизводит его на доске, все проверяют.
5. Подведение итогов и информация о задании на дом.
Преподаватель подводит итог урока с помощью вопросов:
- С каким видом тригонометрических уравнений мы сегодня познакомились?
- Каким способом решаются эти уравнения?
Домашнее задание
Sin x – cos x = 0
4 Sin2 x + 2 cos2 x – 3 sin 2x = 0
Sin x + cos x =1
sin x - cos x =0
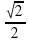
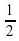 )
)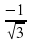 )
)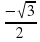 )
)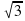
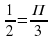 ДА
ДА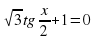
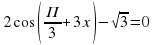
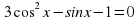
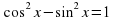
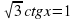
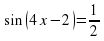

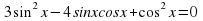
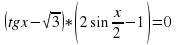
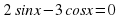
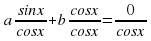
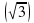 sin x + cos x =0
sin x + cos x =0















