Департамент внутренней и кадровой политики Белгородской области
областное государственное автономное образовательное учреждение
среднего профессионального образования
«Белгородский строительный колледж»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА
математики
по теме «ФУНКЦИЯ»
Разработала:
преподаватель математики
Н.А. Гроза
ТЕМА: «ФУНКЦИЯ»
ЦЕЛЬ УРОКА:
Образовательная – организовать деятельность обучающихся по закреплению определения функции, области определения и области значения функции; рассмотреть способы задания функции; выработать практические навыки применения новых знаний к решению задач.
Развивающая - развивать опыт получения новых знаний на основе уже имеющихся теоретических знаний; содействовать развитию наглядно-образного мышления; способствовать развитию устойчивого интереса к учебному материалу (ОК).
Воспитательная - воспитывать умение и потребность учиться; работать в коллективе (ОК); организовывать собственную деятельность (самостоятельность) (ОК); показать связь математики с окружающим миром и другими науками; воспитывать графическую культуру учащихся.
ТИП УРОКА: изучение нового материала.
ОБОРУДОВАНИЕ:
1. Учебное пособие А. Н. Колмогоров “Алгебра и начала анализа 10-11 класс’’, тетрадь, карандаш, авторучка, линейка.
2. Персональный компьютер, мультимедийный проектор, интерактивная доска.
3.Презентация «Функции», содержащая материал для повторения и закрепления теоретических знаний, для отработки навыков практического применения теории к решению упражнений, создания проблемной ситуации, для самоконтроля.
4.Приложения (самостоятельная работа).
Время проведения: 90 минут
Литература:1. Алгебра и начала анализа. Под ред. Колмогорова А.Н. М.: Просвещение, 1991г.
2. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В., Федорова Н.Е., Шабунин М.И. Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений. 6-е изд. М.:Просвещение, 1998.
3. Барыбин К. С. Методика преподавания алгебры. Пособие для учителей средней школы. М., Просвещение, 1995.
4. Галицкий М. и др. Алгебра и мат.анализ 11 кл. Итоговое повторение. М.: Просвещение, 1998.
СТРУКТУРА УРОКА:
| № | Этап урока | Цель этапа | Время (мин) |
| 1 | Организационный момент | Приветствие, проверка отсутствующих и готовности к уроку | 1 мин. |
| 2 | Этап подготовки и активного изучения новых знаний |
|
| 2.1 | Актуализация | Сообщение новой темы, постановки целей и задач урока. | 2 мин |
| 2.2 | Вводная беседа | Раскрыть важность и актуальность темы. | 2 мин |
| 3 | Изучение нового материала |
|
| 3.1 | Определение функции | Первичное закрепление определения. | 5 |
| 3.2 | Область определения функции | Ввести понятие, первичное закрепление. | 5 |
| 3.3 | Область значения функции | Ввести понятие, первичное закрепление. | 5 |
| 3.4 | Способы задания функции | Рассмотреть основные способы | 5 |
| 3.5 | График функции | Ввести понятие, первичное закрепление. | 5 |
| 4 | Закрепление изученного материала | Обобщение и систематизация новых знаний | 55 |
| 5 | Итоговая беседа. Домашнее задание | Систематизация знаний, полученных на уроке. Инструктаж по домашнему заданию. | 5 мин. |
ХОД УРОКА:
1. Орг. момент. (слайд 1)
Приветствие, проверка присутствующих.
2. Этап подготовки и активного изучения новых знаний
2.1 Актуализация знаний.
Впервые функция вошла в математику под именем «переменная величина» в труде французского математика и философа Рене Декарта «Геометрия» (1637).
Сегодня на уроке мы вспомним такие понятия как функция, область определения и область значения функции; рассмотрим способы задания функции и решим соответствующие задачи.
2.2 Вводная беседа.
Понятие функция одно из важнейших в математике, с их помощью мы описываем реальную жизнь. Например: полет ракеты или изменение прибыли предприятия. Именно свойства функции связывают во едино казалось бы разные методы решения уравнений, неравенств и их систем. Мы будем изучать только числовые функции. Чтобы успешно разобраться с этим понятием нам необходимо овладеть следующими знаниями. (слайд 2)
Задачи урока:
Научиться читать графики функций;
«Узнавать» графики числовых функций;
Рассмотреть способы задания функций;
Научиться находить область определения и значения функции.
3. Этап изучения новых знаний
3.1 Определение функции
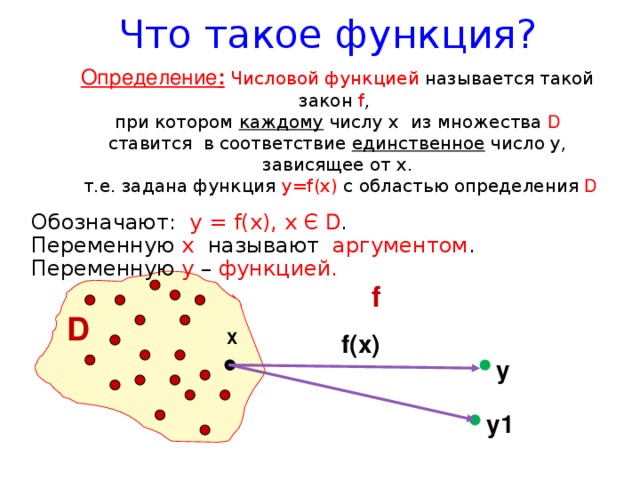
С понятием функции вы знакомы со школы. Итак, вспомним, что такое функция? (ответы учащихся). (слайд 3)
Определение: Числовой функцией называется такой закон f, при котором каждому числу х, из множества D, ставится в соответствие единственное число у, зависящее от х. т.е. задана функция y=f(x) с областью определения D.
Обозначают: у = f(x), x Є D.
Переменную х называют аргументом.
Переменную у – функцией.
Вывод: таким образом, между элементом множества D(х) и у устанавливается единственное соответствие.
(Слайд 4)
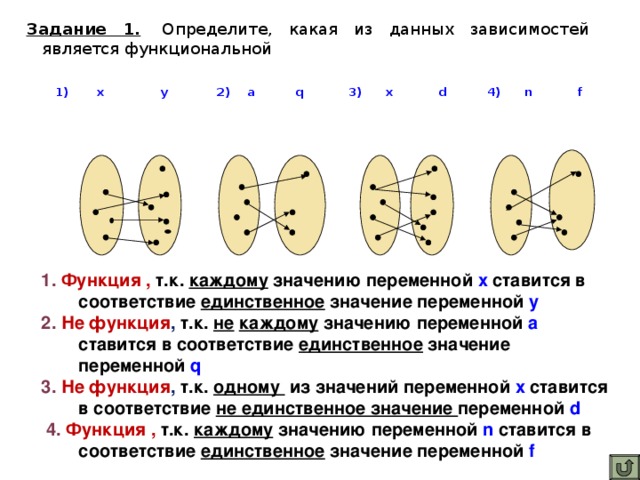
Задание 1. Определите, какая из данных зависимостей является функциональной
1) х у 2) a q 3) x d 4) n f
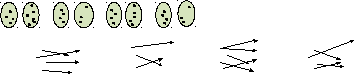
Ответы:
1. Функция, т.к. каждому значению переменной х ставится в соответствие единственное значение переменной у
2. Не функция, т.к. не каждому значению переменной а ставится в соответствие единственное значение переменной q
3. Не функция, т.к. одному из значений переменной х ставится в соответствие не единственное значение переменной d
4. Функция, т.к. каждому значению переменной n ставится в соответствие единственное значение переменной f
3.2 Область определения функции
Для того чтобы работать с функцией одного определения не достаточно. Необходимо знать еще и ее свойства. Вспомним с вами важные свойства функции.
(Слайд 5)
Что называется областью определения функции? (ответы учащихся)
Определение: Областью определения называются все значения, которые принимает аргумент х.
Обозначается: D (f) = Х или D(y).
Пример 1. Найдите область определения функций.
у = 4х – 3. Ответ: D(f)=(-∞;+∞)= R
у = 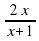 . Ответ: х + 1 ≠ 0, D(f)=(-∞;0) ᴜ (0;+∞) ≠ 1
. Ответ: х + 1 ≠ 0, D(f)=(-∞;0) ᴜ (0;+∞) ≠ 1
у = 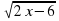 . Ответ: 2х - 6≥ 0, D(f)= [3;+∞).
. Ответ: 2х - 6≥ 0, D(f)= [3;+∞).
3.3 Область значения функции
Следующим важным свойством функции является область значений функции.
(Слайд 6)
Что называется областью значений функции?
Определение: Область значений функции – это множество всех значений функции у.
Обозначают: E(y) или E(f).
Пример 2. Найдите область значений функций.
1) у = х2. Ответ: Е(f)= [0;+∞)= R+
2) у = 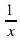 . Ответ: х ≠ 0, Е(f)=(-∞;0) ᴜ (0;+∞)
. Ответ: х ≠ 0, Е(f)=(-∞;0) ᴜ (0;+∞)
3) у = 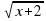 . Ответ: Е(f)= [0;+∞)= R+.
. Ответ: Е(f)= [0;+∞)= R+.
Вывод: область определения и область значения, основные характеристики функции.
3.4 Способы задания функции
Чтобы охарактеризовать функцию (описать все ее свойства), ее необходимо задать. Что значит задать функцию? (ответы учащихся)
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующие значения функции. Существует три основных способа задания функции.
(Слайд 7)
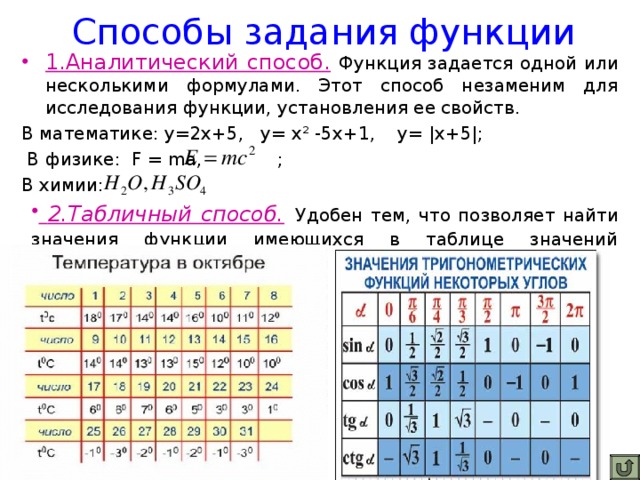
Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
В математике: у=2х+5, у= х² -5х+1, у= |х+5|;
В физике: F = ma, Е = mc2; (называют зависимостью)
В химии: H2O, H2SO4. (носит информационный характер)
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.
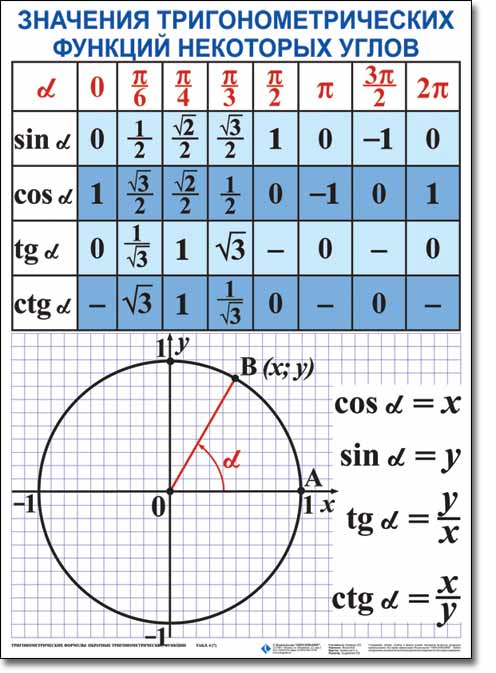

Данный метод очень распространен в науке, технике и т.д. Этот способ определяет функцию не полностью и не дает наглядного изображения характера изменения функции с изменением аргумента.
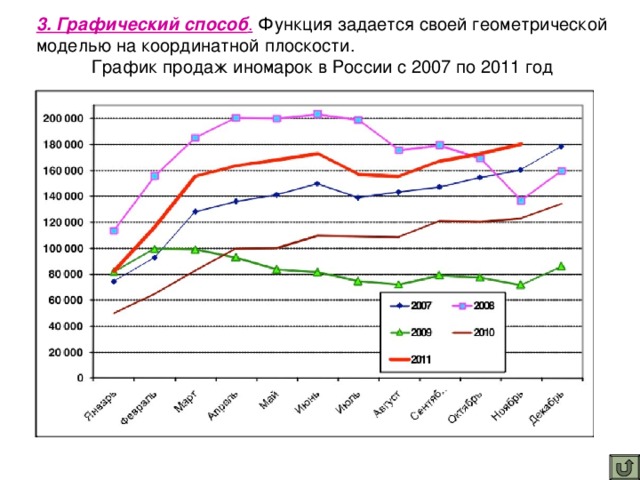
Бывают случаи, когда функциональную зависимость трудно представить с помощью формулы или таблицы. Есть и другой способ задания функции, с которым мы очень часто встречались на уроках алгебры, физики. Это графический способ задания функции. Он является самым наглядным способом представления функции.
(Слайд 8)
График продаж иномарок в России с 2007 по 2011 год
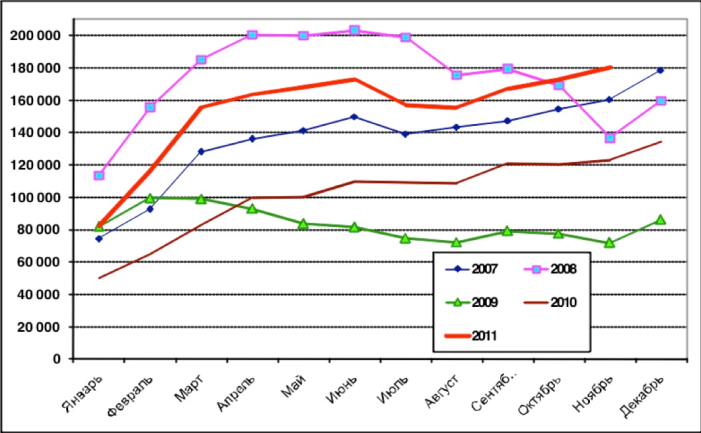
3.5 График функции
Задание функции с помощью графика, используется в неуке и технике, причём иногда график бывает единственно доступным способом задания функции, например при пользовании приборами, автоматически записывающими изменение одной величины в зависимости от изменения другой (барограф, термограф, кардиограф и др.) Так же с помощью графика можно определять свойства функции. Прежде чем рассмотреть такие примеры, давайте вспомним определение графика.
(слайд 9)
Что такое график функции? (Ответы учащихся)
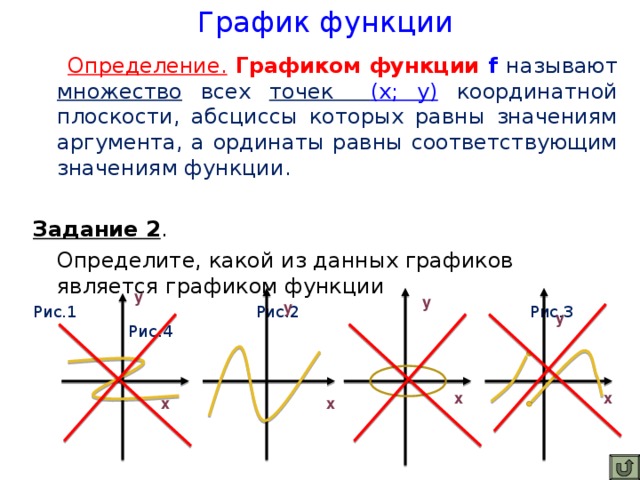
Определение: Графиком функции f называют множество всех точек (х;у) координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты равны соответствующим значениям функции.
Таким образом, аналогично как и в определении функции в определении графика устанавливается единственное соответствие между координатой х и у.
 Задание 2. Определите, какой из данных графиков является графиком функции
Задание 2. Определите, какой из данных графиков является графиком функции
Рис.1 Рис.2 Рис.3 Рис.4
Теперь рассмотрим, как по графику находить область определения и область значения функции.
(Слайд 10)
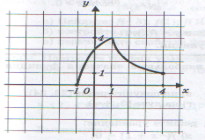
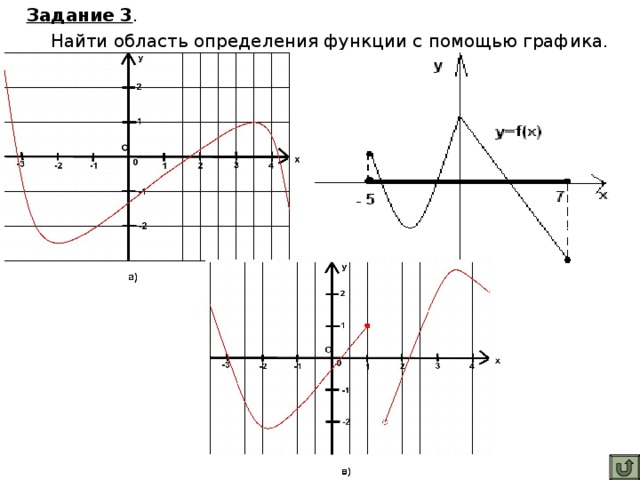
Задание 3. Найти область определения функции с помощью графика.
За область определения отвечают все значения х, поэтому находим по проекции графика на ось Ох. Обсудить с учащимися потом, один записывает у доски ответы.
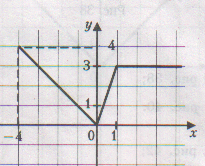
1) 2) 3)
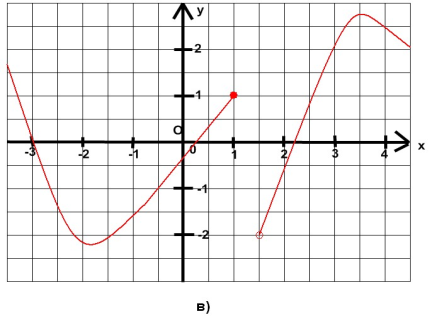
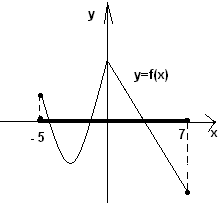
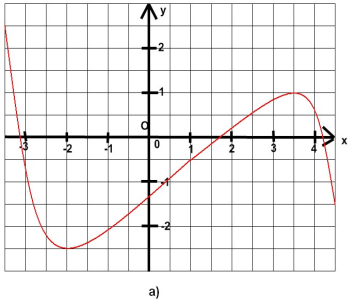
Ответы: 1) D(f)=(-∞;+∞)= R , 2) D(f)= [-5;7], 3) D(f)= (-∞;1]ᴜ(1,5; +∞).
(Слайд 11)
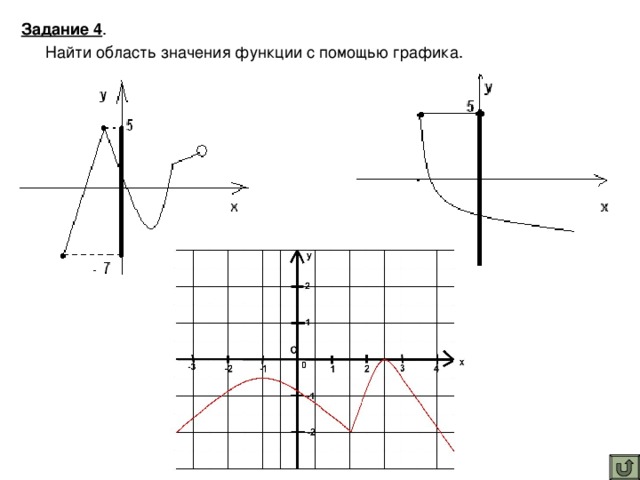
Задание 4. Найти область значения функции с помощью графика.
За область значения отвечают все значения функции у, поэтому находим по проекции графика на ось Оу. Обсудить с учащимися потом, один записывает у доски ответы.
1) 2) 3)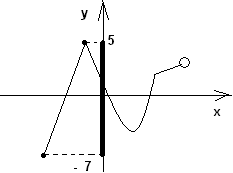
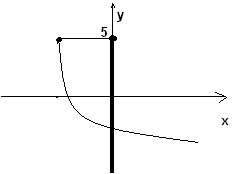
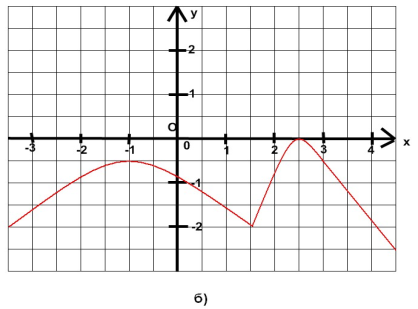
Ответы: 1) Е(f)= [-7;5], 2) D(f)= (-∞;5], 3) D(f)= (-∞;0).
4. Закрепление нового материала
Очень часто на практике приходиться определять значение функции в некоторых точках. Как необходимо это вычислять?
(Слайд 12)
Колмогоров №40. Найдите значение функции:
а) f(x) = x+ 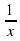 в точках -1, ½, 10. в) f(x) =
в точках -1, ½, 10. в) f(x) = 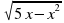 в точках 0, 1, 2.
в точках 0, 1, 2.
Решение: а) f(-1) = -1+ 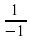 = -2; f(1/2) = 1/2+
= -2; f(1/2) = 1/2+ 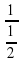 = 2,5; f(10) = 10+
= 2,5; f(10) = 10+ 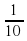 = 10,1.
= 10,1.
в) f(0) = 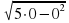 = 0; в) f(1) =
= 0; в) f(1) = 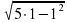 = 2; в) f(2) =
= 2; в) f(2) =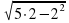 =
= 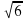 .
.
Самостоятельная работа.
Самостоятельная работа проводится по раздаточным карточкам в 3 вариантах. При необходимости учащиеся пользуются конспектом. (15 минут)
Вариант 1.
Какой из графиков является функцией?
а) б) в)
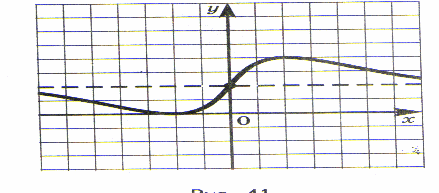
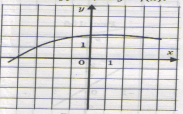
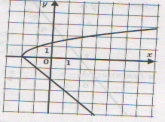
Найдите область определения функций.
а) б) 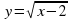
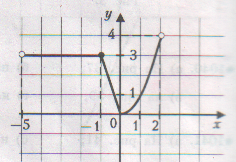
Найдите область значений функций.
а) б) у = х2 + 1
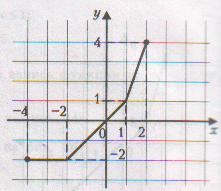
Найти значение функции f (x) = x + 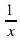 в точках - 1 и 3.
в точках - 1 и 3.
Вариант 2.
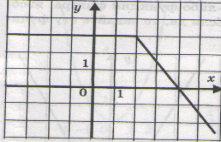
Какой из графиков является функцией?
а) б) в)
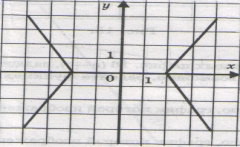
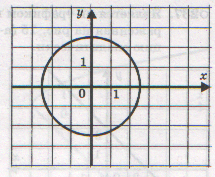
Найдите область определения функций.
а) б) 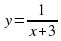
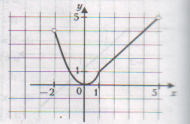
Найдите область значений функций.
а) б)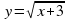
Найти значение функции f (x) = - x + 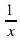 в точках 6 и – 0,5.
в точках 6 и – 0,5.
Вариант 3.
Какой из графиков является функцией?
а) б) в)
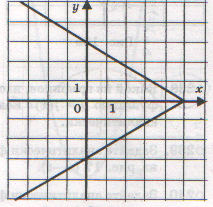
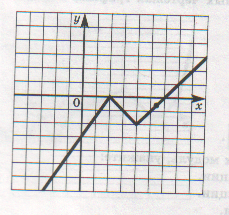
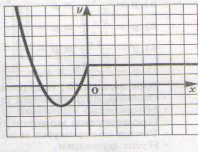
Найдите область определения функций.
а) б)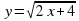
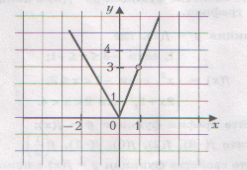
3. Найдите область значений функций.
а) б) у = 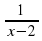
4. Найти значение функции f (x) = x - 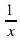 в точках - 5 и 1/4.
в точках - 5 и 1/4.
Игра-конкурс.
Делимся на три команды по рядам выбираем капитанов команд.
В русском языке есть поговорка «Не зная броду, не суйся в воду», как ее можно истолковать применительно к теме «функция»?
(Ответ: нельзя вести разговор о функции, не зная ее области определения) – команды давшие варианты ответов получают дополнительный 1 балл.
А теперь смотрим все на следующий слайд. Функции заданы аналитически, т.е. формулой. Вам необходимо сначала в тетради найти D(f), а затем выйти к доске и записать ответы.
Условия конкурса. Получив верный ответ, член команды выходит к доске и записывает верный ответ рядом с заданием. Экспертами являются капитаны команд. У каждого задания своя цена. После командного состязания конкурс капитанов. Дополнительные баллы тем командам, где участвовало большее количество учащихся.
(Слайд 14) Найти D(f)?
| 1 ряд | 2 ряд | 3 ряд |
| Номер | ответы | Номер | ответы | Номер | ответы |
| 1) у = х2 + 4х – 3 |
| 1) у = 3х2 – 5х -2 |
| 1) у = –х2 + 2х – 10 |
|
| 2) у = 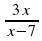 |
| 2) у = 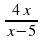 |
| 2) у = 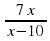 |
|
| 3) у = 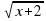 |
| 3) у =  |
| 3) у =  |
|
| 4) у =  |
| 4) у =  |
| 4) у =  |
|
| Для капитанов | Для капитанов | Для капитанов |
| у =  |
| у =  |
| у =  |
|
Также на доске заготовлена таблица для записи результатов и подведения итогов игры.
Стенд результатов игры: максимально 23 балла + дополнительные баллы.
Капитаны команд имеют таблицы с фамилиями членов своей команды, в которой проставляют членам команды отметки за участие и передают учителю (это либо «4», либо «5», либо отметка не ставится вообще).
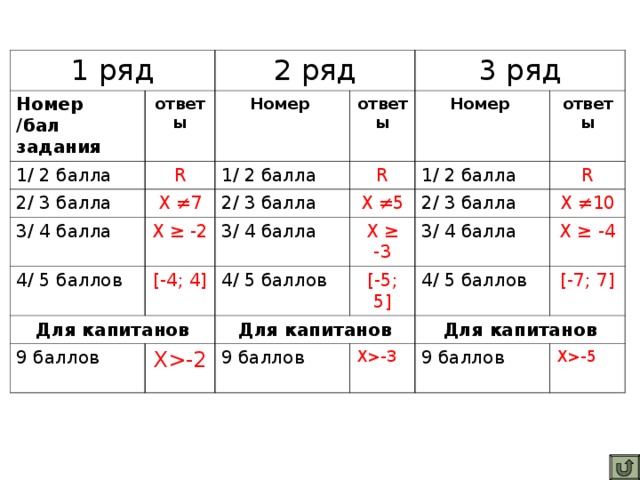
( Слайд 15) Ответы.
| 1 ряд | 2 ряд | 3 ряд |
| Номер /бал задания | ответы | Номер | ответы | Номер | ответы |
| 1/ 2 балла | R | 1/ 2 балла | R | 1/ 2 балла | R |
| 2/ 3 балла | X ≠7 | 2/ 3 балла | X ≠5 | 2/ 3 балла | X ≠10 |
| 3/ 4 балла | X ≥ -2 | 3/ 4 балла | X ≥ -3 | 3/ 4 балла | X ≥ -4 |
| 4/ 5 баллов | [-4; 4] | 4/ 5 баллов | [-5; 5] | 4/ 5 баллов | [-7; 7] |
| Для капитанов | Для капитанов | Для капитанов |
| 9 баллов | X-2 | 9 баллов | X-3 | 9 баллов | X-5 |
Продолжим дальше нашу работу и рассмотрим более сложные задания.
(Слайд 13)
Колмогоров №43. Найдите область определения каждой из функций:
а) f (x) = x –  ; б) f (x) =
; б) f (x) = .
.
Колмогоров №47. Начертите график какой-нибудь функции f, для которой:
а) D(f)= [-2;4], E(f)=[-3;3]; б) D(f)= (-5;3), E(f)=[2;6].
5. Итоговая беседа. Домашнее задание
Сегодня на уроке мы вспомнили:
* Какое соответствие называется функцией?
*Что такое область определения Х и область значения У функции?
*Дайте определение графика функции.
Рефлексия.
Учащиеся заполняют карточки самоанализа изученного материала и сдают учителю.
| | Усвоил(а) хорошо | Иногда ошибаюсь | Пока усвоил плохо |
| Понятие «функция» | | | |
| Область определения функции | | | |
| Область значений функции | | | |
| Что такое график функции? | | | |
Выставление оценок.
Домашнее задание: учебник Колмогоров §2 п.3 №45(б), №51(б)
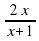 . Ответ: х + 1 ≠ 0, D(f)=(-∞;0) ᴜ (0;+∞) ≠ 1
. Ответ: х + 1 ≠ 0, D(f)=(-∞;0) ᴜ (0;+∞) ≠ 1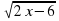 . Ответ: 2х - 6≥ 0, D(f)= [3;+∞).
. Ответ: 2х - 6≥ 0, D(f)= [3;+∞). 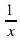 . Ответ: х ≠ 0, Е(f)=(-∞;0) ᴜ (0;+∞)
. Ответ: х ≠ 0, Е(f)=(-∞;0) ᴜ (0;+∞)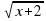 . Ответ: Е(f)= [0;+∞)= R+.
. Ответ: Е(f)= [0;+∞)= R+.


 Задание 2. Определите, какой из данных графиков является графиком функции
Задание 2. Определите, какой из данных графиков является графиком функции


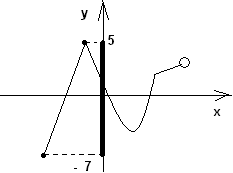


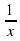 в точках -1, ½, 10. в)
в точках -1, ½, 10. в) 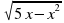 в точках 0, 1, 2.
в точках 0, 1, 2.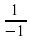 = -2;
= -2; 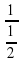 = 2,5;
= 2,5; 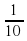 = 10,1.
= 10,1.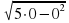 = 0; в)
= 0; в) 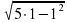 = 2; в)
= 2; в) 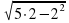 =
= 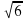 .
.

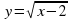

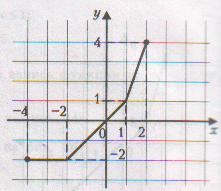



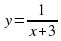

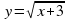




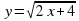

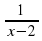

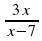
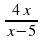
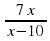







 -2 X ≠10 4/ 5 баллов 9 баллов X ≥ -4 Для капитанов X-3 [-7; 7] 9 баллов X-5" width="640"
-2 X ≠10 4/ 5 баллов 9 баллов X ≥ -4 Для капитанов X-3 [-7; 7] 9 баллов X-5" width="640"