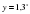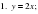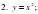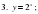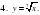Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Методическая разработка урока математики на тему «Показательные уравнения»
Ход урока:
I.Организационный момент: подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей, проверка готовности рабочих мест студентов и учителя, готовности учащихся к работе.)
На первом этапе учитель приветствует студентов, проверяет готовность группы к работе.
II Актуализация знаний обучающихся
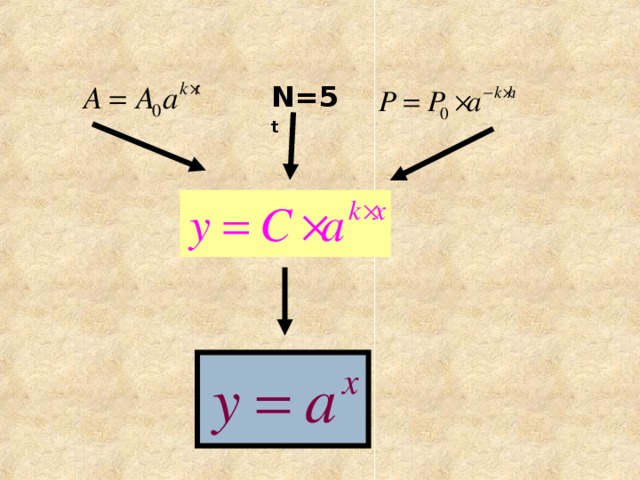
Тема урока « Показательные уравнения» (слайд 1)
А эпиграфом к нашему уроку станут слова С. Коваля: «Уравнения – это золотой ключ, открывающий все математические сезамы». Т. е. другими словами можно сказать, что если вы будете уметь решать уравнения, то экзамена по математике вам не стоит бояться.
А какие вообще виды уравнений вы знаете? (Рациональные, дробно – рациональные, тригонометрические, иррациональные, показательные)
Давайте сыграем с вами в следующую игру.
Игра «Кто быстрее»
Эта игра проводится с целью актуализации знаний студентов.
Студенту предлагается в течение 60 секунд отвечать на вопросы. (листочки розданы заранее)
Звание «знатока на уроке» присваивается тому, кто ответил на большее количество вопросов. (итог в конце урока).
---------
Пример 1.
22х - 8х+1 = 0
Рассмотрим основания. Они разные! Два и восемь. Вспомним, что
8 = 23
Можно записать:
8х+1 = (23)х+1
Вспомним
(аn)m = anm,
получается:
8х+1 = (23)х+1 = 23(х+1)
Исходный пример стал выглядеть вот так:
22х - 23(х+1) = 0
Переносим 23(х+1) вправо получаем:
22х = 23(х+1)
Убираем основания:
2х = 3(х+1)
Решаем и получаем
х = -3
Ответ: х = -3
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Метод разраб показательные уравнения»
Просмотр содержимого презентации
«Презент к показательные уравнения»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2020 руб.
2880 руб.
1900 руб.
2710 руб.
2020 руб.
2880 руб.
1760 руб.
2510 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
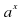 =b, где а0, а≠1 .
=b, где а0, а≠1 .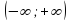 функция возрастает при а1и убывает при 00,а0, а≠1 уравнение
функция возрастает при а1и убывает при 00,а0, а≠1 уравнение 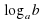 . Решение показательного уравнения основано на том, что это уравнение равносильно уравнению f(x)=g(x).
. Решение показательного уравнения основано на том, что это уравнение равносильно уравнению f(x)=g(x).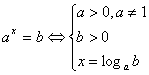
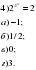
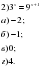
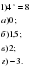
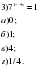 5.Устная работа. Давайте устно решим уравнения
5.Устная работа. Давайте устно решим уравнения новой переменной.
новой переменной.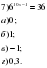
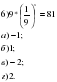
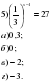 t2 -8t -9 =0
t2 -8t -9 =0
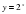 ;
; 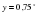 ;
; 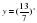 ;
; 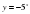 ;
; 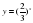 ;
; 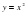 ;
; 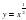 ;
; 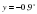 ;
; 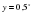 ;
;