| Постановка проблемы | Добрый день, ребята. Забор нашего учебно-опытного участка обветшал и нам необходимо его обновить. Строили участок давно, и никто не помнит его размеров. Рабочий вспомнил, что ограждение трех сторон, поскольку наш участок с западной стороны примыкает к участку местных жителей и не огораживается, составило 240 м. Помогите оценить размеры нашего участка, если его площадь не меньше 4000 м кв., а ширина минимальна РЕШЕНИЕ: Понятно, что участок будет огорожен с трех сторон. Пусть ширина равна х м, тогда длина будет равна (240-2х) м. Отсюда площадь: S = х ( 240-2х)= -2х2+ 240х (м2). По условию S ≥ 4000 м2, поэтому -2х2 + 240х - 4000 ≥ 0. | Отвечают
|
| Определение темы урока, Цели, задач урока | Посмотрите на него. Как вы думаете, как оно называется? Тогда сформулируйте тему урока. Верно тема урока квадратные неравенства. Впишите тему урока в рабочий лист, с которым мы сегодня работаем. В ваших рабочих листах напротив заданий имеется колонка для самооценки, выполняя задания на уроке, вам предстоит оценить свою работу по заданным критериям, в конце урока посчитаем количество набранных баллов и определим отметку по шкале в конце рабочего листа. Кто знает, как решить квадратное неравенство? Тогда сформулируйте цель урока. Что для этого необходимо сделать? Сформулируйте задачи урока: - сформулировать определение квадратного неравенства, - познакомиться с алгоритмом решения квадратного неравенства, - научиться применять алгоритм при решении неравенств. |
Формулируют тему урока
Цель – научиться решать квадратные неравенства.
|
| Определение квадратного неравенства | Используя памятку «Определение» и прочитав 1 абзац п 34, определите ключевые слова и сформулируйте определение квадратного неравенства, впишите его в рабочий лист. Проверим, что получилось, подчеркивая ключевые слова. Если вы верно определили ключевые слова, поставьте себе 1 балл в колонку самооценка, иначе 0 баллов Используя определение, найдите на слайде квадратные неравенства, запишите в рабочие листы буквы, рядом с которыми квадратные неравенства. Проверяем: квадратные неравенства под буквами а - и. поставьте себе в рабочий лист 1 балл, если задание выполнили верно, иначе 0 баллов. |
Формулируют определение |
| Поиск решения неравенств | 1 Задача решена, переходим к решению второй задачи. Всем необходимым для решения таких неравенств мы с вами располагаем, в чем сейчас убедимся. Рассмотрим неравенство х2 + 2х – 3 0 Что видим в левой части неравенства? - квадратный трехчлен. Верно, если рассмотреть функцию у= х2 + 2х – 3, то что является ее графим? Парабола. Знаком ли нам алгоритм построения параболы? Да. Давайте построим график этой функции по данному алгоритму. Вершина х0=-в/2а=-2/2=-1 У0=1-2-3=-4 Ось симметрии х=-1 Ветви направлены вверх Таблица | х | 0 | 1 | 2 | -2 | -3 | -4 | | у | -3 | 0 | 4 | -3 | 0 | 4 | Определите, на каких промежутках оси х ординаты графика то есть у больше нуля, то есть положительны, и на каких меньше нуля, то есть отрицательны. Решим неравенства. Подведем итог. Что важно для нас в графике для того чтобы решить неравенство? Вершина нам потребовалась? Нет Точки пересечения графика с осью х? Да Направление ветвей параболы? Да Поработайте в паре и сформулируем алгоритм решения квадратного неравенства, используя чтение с пометками стр 217. Запишите алгоритм в рабочие листы. Не забываете правила работы в группе, паре. Проверим, что у вас получилось. Если вы определили основные этапы алгоритма, поставьте себе 1 балл, иначе– 0 баллов |
1 учащийся у доски строит параболу
|
| Применение алгоритма | Мы решили 2 задачу, сформулировали алгоритм решения квадратных неравенств графическим методом, на последующих уроках мы познакомимся еще с одним методом, а пока мы переходим к решению 3. Используя алгоритм, решим неравенство х2 + 2х – 3 Если вы выполнили задание верно, поставьте 1 балл, иначе – 0 баллов. |
1 учащийся у доски решает неравенство по алгоритму |
| Исследование решений в зависимости от направления ветвей параболы и дискриминанта | Мы уже вспомнили, что в зависимость от коэффициента а ветви параболы могут быть направлены вверх или вниз. А какие случаи возможны при решении квадратного уравнения в зависимости от дискриминанта? Исследуем квадратные неравенства в зависимости от коэффициента а и D В ваших рабочих листах сделайте наброски графиков в зависимости от значений а и D. И запишите ответ для решения неравенства со знаком 0.
| По одному выходят к доске и рисуют набросок графика, определяют ответ неравенства |
| Решение задач | Используя алгоритм решения неравенства и нашу схему, решите самостоятельно №34.3 (а,б), №34.4 (а,б) учебника. У части ребят уже имеются частичные записи решения и вам необходимо заполнить пропуски, остальные решают только с опорой на алгоритм. Обменяйтесь рабочими листами с соседом по парте. Проверим решение по эталону: За каждый правильный ответ поставьте 1 балл. То есть всего за выполнение этого задания вы можете набрать максимально 4 балла. |
Решают.
Взаимооценка |
| Решают задачу ОГЭ | Кто закончил, выясните в сети Интернет, есть ли квадратные неравенства на ОГЭ?
| Да, в задании № 14 |
| Рефлексия | Вернемся к нашей задаче об учебно-опытном участке. Можем ли сейчас решить задачу, с которой столкнулись в начале урока? Решите неравенство. -2х2 + 240х - 4000 ≥ 0. Решив неравенство, имеем : 20 ≤ x ≤ 100. Так как ширина должна быть минимальна, то она равна 20 м, значит, длина должна быть не менее 200 м. Если вы справились с этой задачей, поставьте себе 1 балл |
1 решает у доски |
| Д/З | Запишите домашнее задание. Заполните нашу таблицу с исследованием для неравенства со знаком П34., № 34.3 (в,г), №34.4 (в,г). Дополнительное задание: найти из открытого банка ОГЭ квадратное неравенство, которое вы бы смогли решить, используя теоретический материал, изученный сегодня на уроке и решите его. |
|
| Оценивание работы | Посчитайте количество баллов в столбце самооценка и по шкале в конце рабочего листа выставите себе оценку. С учетом ваших оценок я выставлю вам отметку за урок. Оцените свою работу на уроке: поднимите  - цель достигнута - цель достигнута
 - справляюсь, но есть ошибки - справляюсь, но есть ошибки
 - ещё нужно над этим работать - ещё нужно над этим работать |
|
| № | Задание | Решение | Самооценка |
| 1 | Прочитав 1 абзац п 34 (стр 214), определите ключевые слова, сформулируйте определение квадратного неравенства. | ОПРЕДЕЛЕНИЕ: Квадратное неравенство – это_______________ __________________________________________ __________________________________________ __________________________________________ __________________________________________ |
|
| 2 | Используя определение, найдите на рисунках а-л квадратные неравенства, запишите в рабочие листы буквы, над которыми изображены данные неравенства. | Квадратные неравенства: ________________________________________ |
|
| 3 | Постройте график функции у= х2 + 2х – 3
Алгоритм: Вершина х0 = 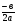 , у0. , у0. х0=
у0=
Ось симметрии х=х0 х= Направление ветвей _______________________ Таблица
| а) х2 + 2х – 3 0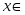 б) х2 + 2х – 3 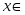 в) х2 + 2х – 3 ≤ 0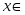 г) х2 + 2х – 3 ≥ 0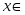 
|
|
| 4 | Сформулируйте алгоритм решения квадратного неравенства | 1.__________________________________________________________________________________________ ____________________________________________________________________________________________ 2_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 3_______________________________________________________________________________________________________________________________________________________________________________________ 4__________________________________________ |
|
| 5 | Используя алгоритм, решим неравенство х2 + 2х – 3
|
|
|
| 6 | 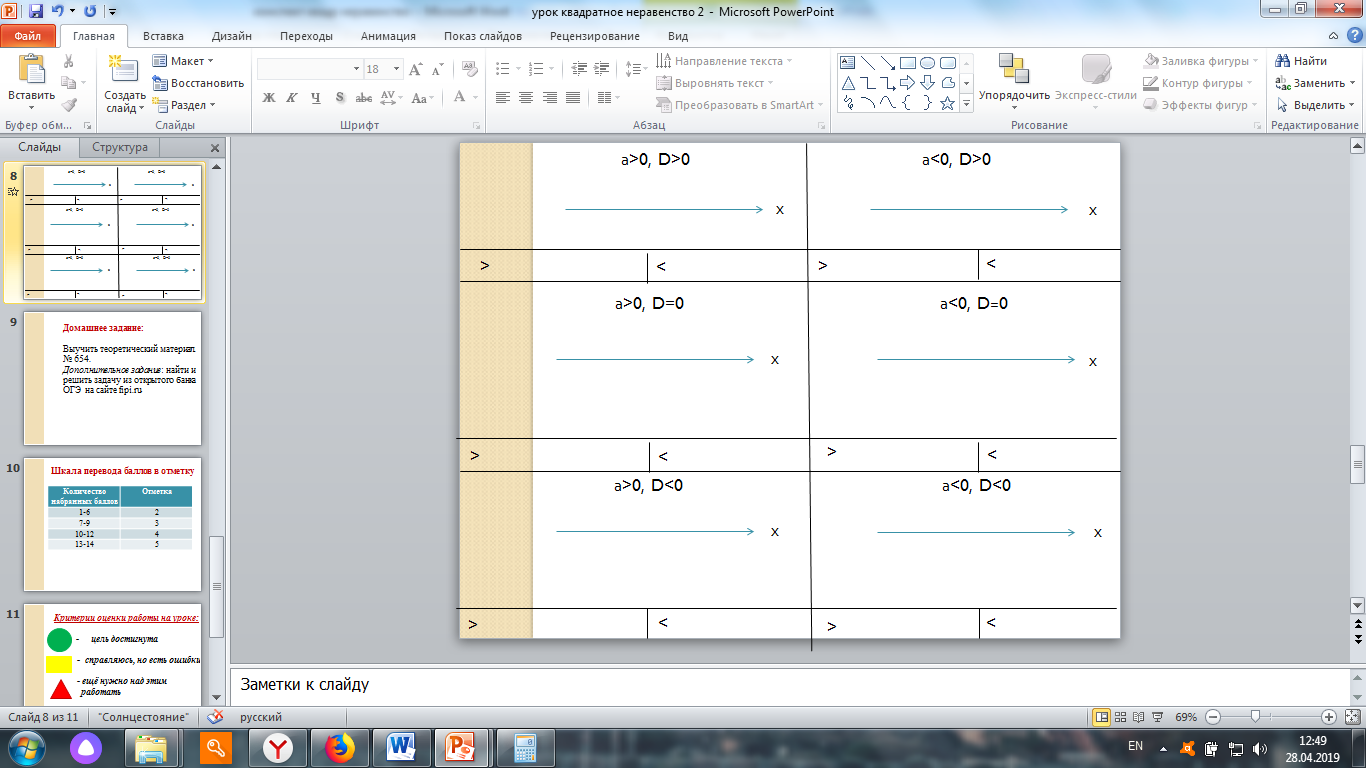
|
|
| 7 | Решить квадратные неравенства №34.3 (а,б), №34.4 (а,б) | №34.3 (а) -х2 + 6х – 5 Корни уравнения -х2 + 6х – 5 = 0
Ветви направлены _________________ Набросок:

Ответ. х №34.3 (б) -х2 - 2х +8 ≥ 0 Корни уравнения -х2 – 2х +8 = 0
Ветви направлены__________ Набросок:

Ответ. х №34.4 (а) 2х2 - х – 6 0 Корни уравнения -х2 + 6х – 3 = 0
Ветви направлены _______________ Набросок:

Ответ. х №34.4 (б) 3х2 – 7х +4 ≤ 0 Корни уравнения -х2 + 6х – 3 = 0
Ветви направлены ___________________ Набросок:

Ответ. х
|
|
| 7 | Решить квадратные неравенства №34.3 (а,б), №34.4 (а,б) | №34.3 (а) -х2 + 6х – 5 Корни уравнения -х2 + 6х – 5 = 0
Ветви направлены _________________ Набросок:

Ответ. х №34.3 (б) -х2 - 2х +8 ≥ 0
Ответ. х №34.4 (а) 2х2 - х – 6 0
Ответ. х №34.4 (б) 3х2 – 7х +4 ≤ 0
Ответ. х
|
|
| 8 | Решить задачу |
|
|
 - цель достигнута
- цель достигнута  , у0.
, у0.



















