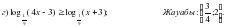Саба?ты? та?ырыбы: Логарифмдік те?сіздіктер.
К?ні: 19.02
Ма?саты: Логарифмдік те?сіздіктерді шешуді ме?герту
Аны?тама: Айнымалысы логарифм та?басыны? ішінде болатын те?сіздікті логарифмдік те?сіздік деп атайды.
или
Для решения таких неравенств, учитывая область определения логарифмической функции и ее свойства, применяют следующие утверждения:
- при а > 1 неравенство равносильно системе неравенств:
(1)
- при 0 < а < 1 1 неравенство равносильно системе неравенств:
(2)
Мысалы:
Шешуі:Логарифмні? ?асиетінен: .
( б?л м?мкін м?ндер жиынын табу ?шін керек.)
Жауабы:
1.Функцияны? аны?талу облысын табы?дар.
1. 2. 3.
4. 5. 6.
7. 8. 9.
10. 11. 12.
13.
14. Те?сіздікті шеші?дер:
Мысал №1:
Шешуі: а =,
(2): немесе
Жауабы :
№2.
а = 10 > 1,
Жауабы:
Дидактикалы? материалдар :
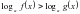 или
или 
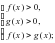 (1)
(1) (2)
(2)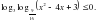
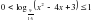 .
. 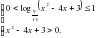
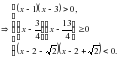
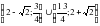
 2.
2.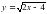 3.
3. 
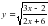 5.
5. 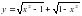 6.
6. 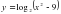
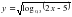 8.
8. 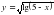 9.
9. 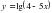
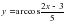 11.
11. 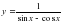 12 .
12 . 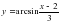



 а =
а =  ,
, 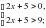 немесе
немесе 
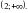 Жауабы :
Жауабы : 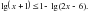

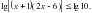
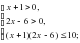

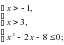

 Жауабы:
Жауабы: