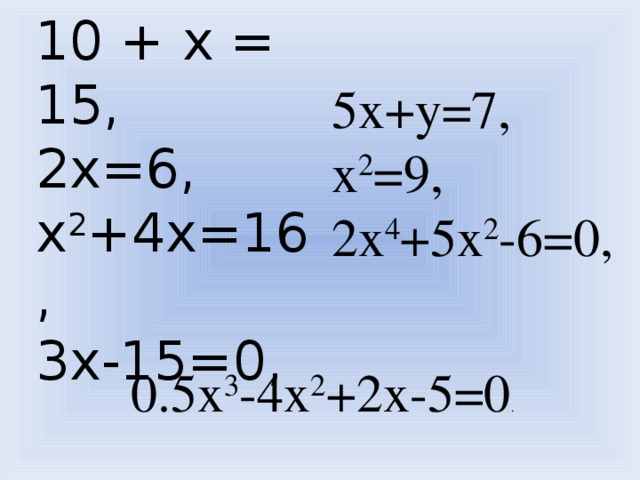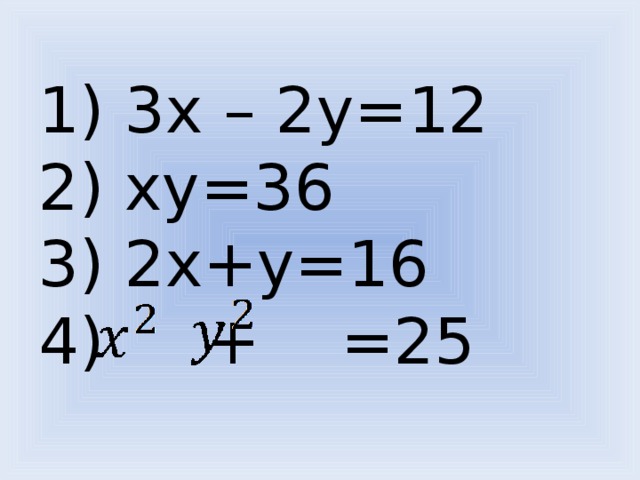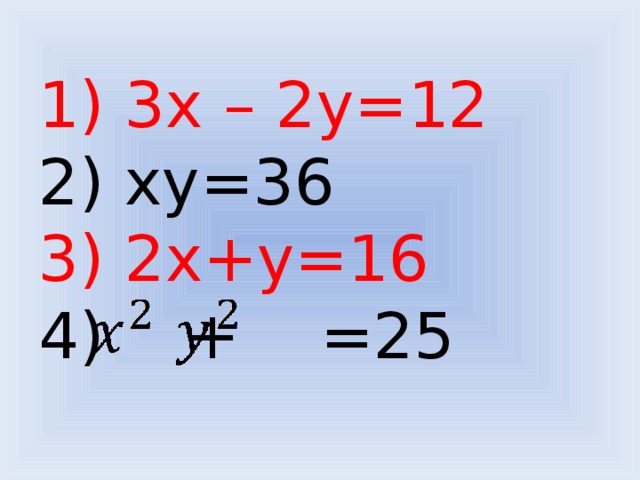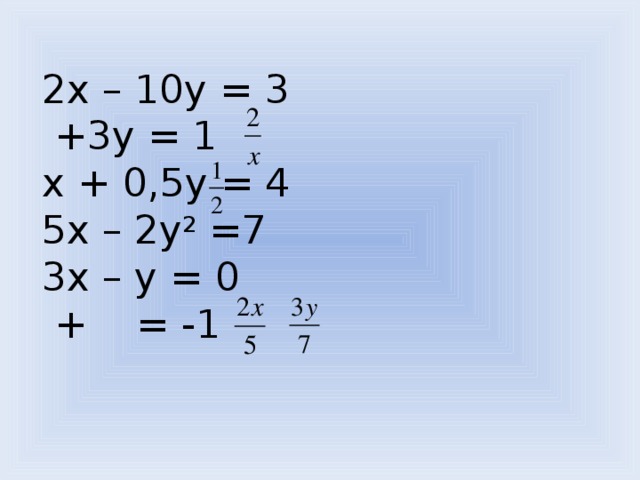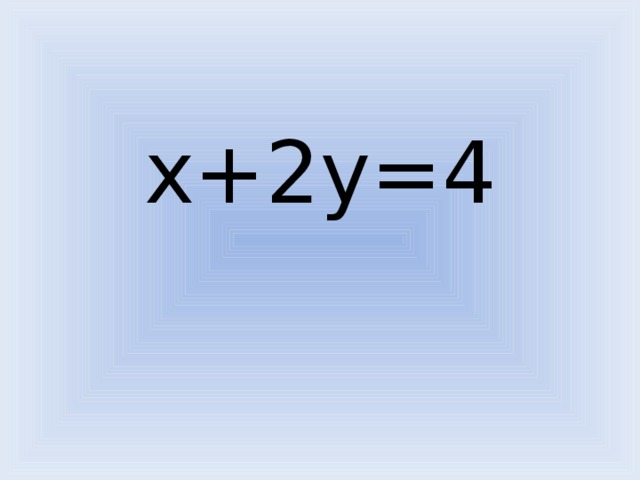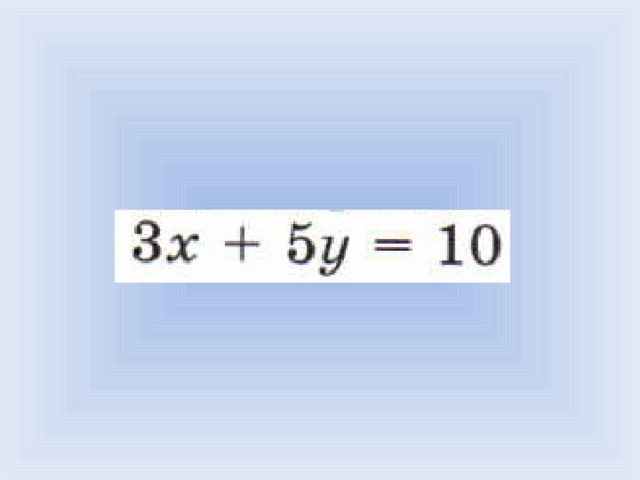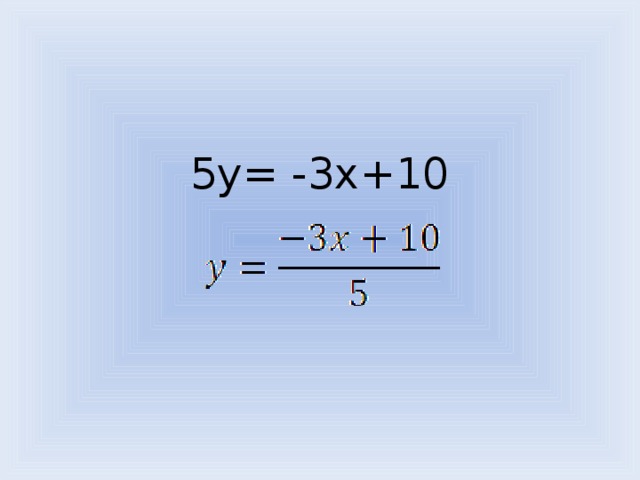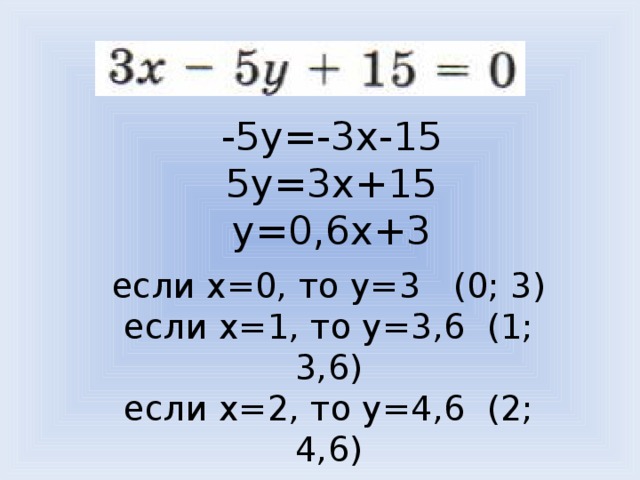Конспект урока математики в 8 классе «Линейные уравнения с двумя переменными»
Тип урока: урок ознакомления с новым материалом
Цель: расширить понятийную базу по теме «Линейное уравнение с двумя переменными», вывести алгоритм решения линейного уравнения с двумя переменными.
Задачи:
обучающие:
создать условия
- для формирования понятий: «уравнение с двумя переменными», «решение уравнения с двумя переменными», «линейное уравнение с двумя переменными»;
- для получения алгоритма решения линейного уравнения с двумя переменными.
развивающие:
- для развития умения работать с новой информацией;
- для развития умения делать выводы, рассуждения;
- для развития способности к рефлексии.
воспитательные:
- для воспитания познавательного интереса к открытию новых знаний и применения их в практической деятельности.
Методы обучения: наглядный (демонстрация презентации), словесный, проблемно-поисковый, практический.
Формы организации: фронтальная, индивидуальная.
Оборудование: интерактивная доска, мультимедийный проектор, компьютер.
Содержание урока:
Организационный момент: здравствуйте, ребята.
Получать новые знания то же самое, что покорять горные вершины. Сегодня мы будем покорять вершину математических знаний [слайд 1].
В путешествии нам потребуется журнал маршрута [слайд 2].
Актуализация прежних знаний
Откроем его [слайд 3]. Что мы видим?
10+x=15, 2x=6, x2+4x=16, 3x-15=0, 5x+y=7, x2=9, 2x4+5x2-6=0, 0.5x3-4x2+2x-5=0.
-Уравнения.
- А что такое уравнение?
- Уравнение – это равенство, содержащее переменную.
Какие уравнения вам известны? Назовите.
Называют. Какое это уравнение?
Линейные, квадратные, кубические, биквадратные, и т. д.
Какое уравнение осталось? 5x+y=7, чем оно отличается?
Оно содержит две переменных.
Определение темы и цели урока.
На этом уроке мы рассмотрим уравнения с двумя переменными.
Запишите в тетрадях число и тему урока: «Линейные уравнения с двумя переменными» [слайд 4]
А теперь сформулируем цель урока.
Цель: узнать, что такое линейное уравнение с двумя переменными, найти способы его решения [слайд 5]
Ознакомление с новым материалом:
Перед нами первая ступень горной вершины знаний
Пробные учебные действия, приводящие к понятию уравнения с двумя переменными, решения уравнения с двумя переменными и линейного уравнения с двумя переменными.
На доске представлены задачи [слайд 6]
1) Разность утроенного первого числа и удвоенного второго числа равна 12.
Найдите эти числа.
2) Площадь прямоугольника равна 36 см2. Каковы длины сторон?
3) Периметр равнобедренного треугольника равен 16 см. Чему равны длины его сторон?
4) Гипотенуза прямоугольного треугольника равна 5 см. Чему равны его катеты?
Нужно перевести их на математический язык. Обратите внимание на то, что для перевода этих задач на математический язык необходимо ввести две переменные, например, x и y. (пусть пробует дети без подсказки).
Разбор каждой задачи с записью на доске.
Сверим наши записи с журналом маршрута [слайд 7].
1) 3х – 2у=12
2) ху=36
3) 2х+у=16
4) x2+y2 =25
Если есть ошибки проанализировать и
Запишем в тетрадях результат.
Такие равенства называются уравнениями с двумя неизвестными.
Сформулируем определение уравнения с двумя переменными.
Формулировка определения учениками.
Запишем определение из журнала маршрута [слайд 8].
уравнением с двумя переменными называется равенство, содержащее две неизвестные величины.
Перед нами вторая ступень горной вершины и новое испытание.
Давайте к каждому из составленных уравнений подберём пару чисел, чтобы равенство было верным.
Учащиеся называют пары чисел, учитель записывает на доске.
Только ли положительные числа являются решением уравнений?
Записываем.
Полученные пары являются решениями данных уравнений с двумя переменными.
Сформулируем определение решения уравнения с двумя переменными.
Формулировка определения учениками.
Запишем определение из журнала нашего маршрута [слайд 9].
решением уравнения с двумя переменными называется всякая пара значений переменных, которая обращает это уравнение в верное числовое равенство
А сейчас перед нами третья ступень горной вершины.
Вспомним вторую задачу [слайд 10].
Обратите внимание на то, что отрицательные корни не являются решением этой задачи
[слайд 11]. Рассмотрим первое и третье уравнение, чем они похожи и чем отличаются от других.
Такие уравнения являются линейными.
Сформулируем определение линейного уравнения с двумя переменными.
Формулировка определения учениками.
Запишем определение из журнала маршрута [слайд 12].
линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где a,b,c произвольные числа.
А вот и четвёртая ступень горной вершины.
Построение алгоритма решения линейного уравнения с двумя переменными и его первичное закрепление
Определите, какие из следующих уравнений являются линейными с двумя переменными [слайд 13].
2х – 10у = 3
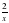 +3у = 1
+3у = 1
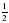 х + 0,5у = 4
х + 0,5у = 4
5х – 2у2 =7
3х – у = 0
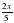 +
+ 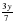 = -1
= -1
А сейчас попробуем решить линейное уравнение [слайд 14].
x+2y=4
Применим метод подбора.
Записать на доске.
Существует более простой способ решения линейных уравнений с двумя переменными. (варианты)
Посмотрим в журнал маршрута и запишем [слайд 15].
Для нахождения решений линейного уравнения с двумя переменными можно выражать одну переменную через другую.
Попробуем решить ещё одно уравнение [слайд 16]. 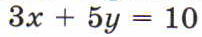 Решите уравнение относительно Y.
Решите уравнение относительно Y.
Проверим по журналу маршрута [слайд 17].
Подберите несколько пар чисел, которые являются решением данного уравнения.
Минутка релаксации с цветотерапией
Перед самыми трудными испытаниями сделаем привал, отдохнём. [слайд 18].
Осмысление и закрепление нового материала (самостоятельная работа с самопроверкой по эталону).
Мы подошли к самым трудным ступеням, которые вы должны пройти самостоятельно. Решают номера [слайд 19]. №571 (а,в), 574.
[слайд 20] №575
Сравним ваши решения с журналом маршрута [слайд 21]
Подведение итогов.
Вот мы с вами и добрались до вершины [слайд 22]. Вспомните цель нашего урока, достигли ли мы её? Что помогло нам добиться успеха? С каким новым понятием мы познакомились? Что для вас было самым сложным на уроке? Какие качества характера помогли нам справиться с этими трудностями.
Выставление оценок.
Рефлексия «Плюс, минус»
Ребята заполните анкеты, в которых подчеркните тот вариант, который вам подходит для оценки нашего урока.
| 1.На уроке я работал
2.Своей работой на уроке я
3.Узнал на уроке
4.За урок я
5.Мое настроение
6.Материал урока я | активно / пассивно
доволен / не доволен
много нового/ ничего нового не узнал
не устал / устал
стало лучше / стало хуже
понял / не понял |
Домашнее задание: А маршрут выполнения домашнего задания будет зависеть от того, какую оценку вы хотите получить. На 5, на 4 и на 3.
№ 572, 573, 577
На память о нашем восхождении к вершине примите в подарок фото, на котором есть определение линейного уравнения и алгоритм его решения. Вы можете им пользоваться при подготовке домашнего задания, а также заучить его в качестве основного правила.
Литература:
1. Дорофеев Г.В. и др. Алгебра, 8 класс: учебник для общеобразовательных организаций. – М. : Просвещение, 2010. – 288 с.
2. Дюмина Т. Ю. Алгебра. 8 класс: поурочные планы по учебнику под редакцией Г.В. Дорофеева. 2 полугодие. – Волгоград: Учитель, 2011. – 253 с.
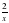 +3у = 1
+3у = 1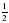 х + 0,5у = 4
х + 0,5у = 4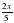 +
+ 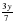 = -1
= -1