«Линейная функция и ее график»

Хчаян Ирина Николаевна алгебра 7 класс дата________________

Тема урока: «Линейная функция и ее график»

Тип урока: урок обобщения и систематизации знаний

Цель урока: осуществить повторение, обобщение и систематизацию материала темы, выявить уровень усвоения знаний и умений.

Задачи:

1) образовательная: выработка у учащихся умения обобщать изученный ранее материал, анализиро­вать, сопоставлять, делать выводы, переносить знания в измененную ситуацию;

2) воспитательная: повышение интереса к изучаемой теме, познавательного интереса к предмету, воспитание аккуратности при выполнении работы; формирование чувства ответственности за результат работы;

3) разви­вающая: развитие умения применять ранее полученные знания, формировать навыки самоконтроля, навыки работы в коллективе.

Ход урока

I.Организационный момент.

II. Проверка домашнего задания

№8.21(а,б)

№8.27(в,г)

III. Устная работа

1. Фронтальный опрос.

- Какой формулой задается график линейной функции? (у = kx + b)

- Что обозначает х в данной формуле? (Это независимая переменная.)

- Что такое k и b (Некоторые числа, причем к - угловой коэффициент)

- Дайте определение линейной функции. (Линейной функцией называется функция, которую можно задать формулой вида у = k х + b, где х - независимая переменная, k и b некоторые числа.)

- Является ли линейной функция, заданная формулой:

а) ; б) ;

в) ; г) ;

д) ?

Для этих формул укажите коэффициенты k и b. (Формулы, таблицы проецируются на экран)

- Что является графиком линейной функции? (Прямая)

- Сколько точек необходимо для построения прямой? (Две точки)

2. Заполните пустые графы таблицы, если известна функция у = 3х -2

х	-3	•	•	0	•	2	•
у	•	-8	-5	•	1	•	7

х	-3	-2	-1	0	1	2	3
у	-11	-8	-5	-2	1	4	7

3. Не строя графика, найдите координаты точек, через которые проходит график линейной функции у = -2х + 5, если известны абсциссы 3 и -2.

Решение: если х = 3,то у= -2•3 + 5 = -1. Значит, координаты точки с абсциссой 3 (3; -1). Если х = -2, то у = -2 • (-2) + 5 = 9. Значит, координаты точки с абсциссой -2 (-2; 9).

Ответы: (3; -1), (-2; 9).

IV. Выполнение заданий (выполняем задания на доске и в тетрадях)

1. Линейная функция задана формулой у = - 0,3х + 7. Найдите:

1) Значение у, если х = -2; 3; 1.

Решение:

Если х = -2, то у = -0,3• (-2) + 7 = 7,6.

Если х = 3, то у = -0,3 • 3 + 7 = 6,1.

Если х =1, то у = -0,3•1 + 7 = 6,7.

Ответы: 7,6; 6,1; 6,7.

2) Значение х, при котором у = - 9 ,8; 0.

Решение:

Если у = -9,8, то -9,8 = - 0,3х + 7. Решим полученное уравнение:

-0,Зх + 7 = -9,8;

-0,Зх = -9,8 -7;

-0,3х = -16,8;

х = 56.

Если у = 0, то 0 = - 0,Зх + 7.

Решим полученное уравнение: - 0,3 х + 7=0;

-0,Зх = -7;

х = 23 1/3

Ответы: 56; 231/3.

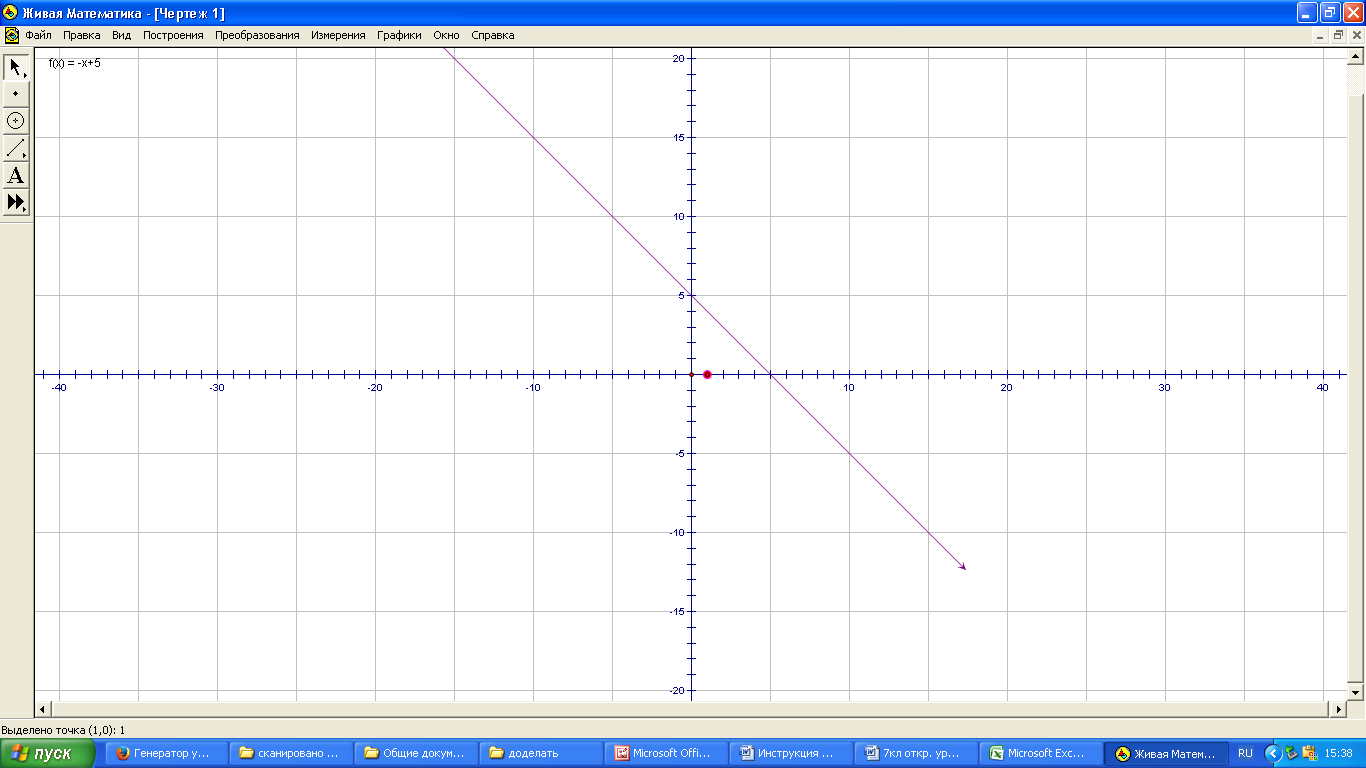
2. Постройте график функции у = - х + 5.

Решение: составим таблицу значений:

х	-2	4
у	7	1

Построим график функции:

3. Проходит ли график функции у = 2х + 4 через точки А (1;6), В (-5; 7)?

Решение:

Если А (1; 6), то х = 1, а у = 6. Подставим одно из значений в формулу линейной функции.

Если х =1,то у = 2• 1+4 = 6. Значит, точка А (1; 6) принадлежит графику функции у = 2х+4.

Если В (-5; 7), то х = -5, а у = 7. Подставим одно из значений в формулу линейной функции.

Если х = -5, то у = 2 • (-5) + 4 = -6. Значит, точка В (-5; 7) не принадлежит графику функции у = 2х + 4.

Следовательно, график функции у = 2х + 4 проходит через точку А(1;6).

Ответ: А (1; 6).

4. Не выполняя построения графика функции у = 2,5х - 3, найдите координаты точек пересечения с осями координат.

Решение:

Если график функции пересекает ось ординат, то абсцисса равна 0.

Если х = 0, то у = 2,5 • 0 - 3 = -3. Следовательно, график функции пересекает ось ординат в точке (0; -3).

Если график функции пересекает ось абсцисс, то ордината равна 0.

Если у = 0, то 0 = 2,5х-3.

Решим получившееся уравнение: 2,5х -3 = 0; 2,5х = 3; х = 1,2.

Следовательно, график функции пересекает ось абсцисс в то (1,2; 0).

Ответ: (0; -3), (1,2; 0).

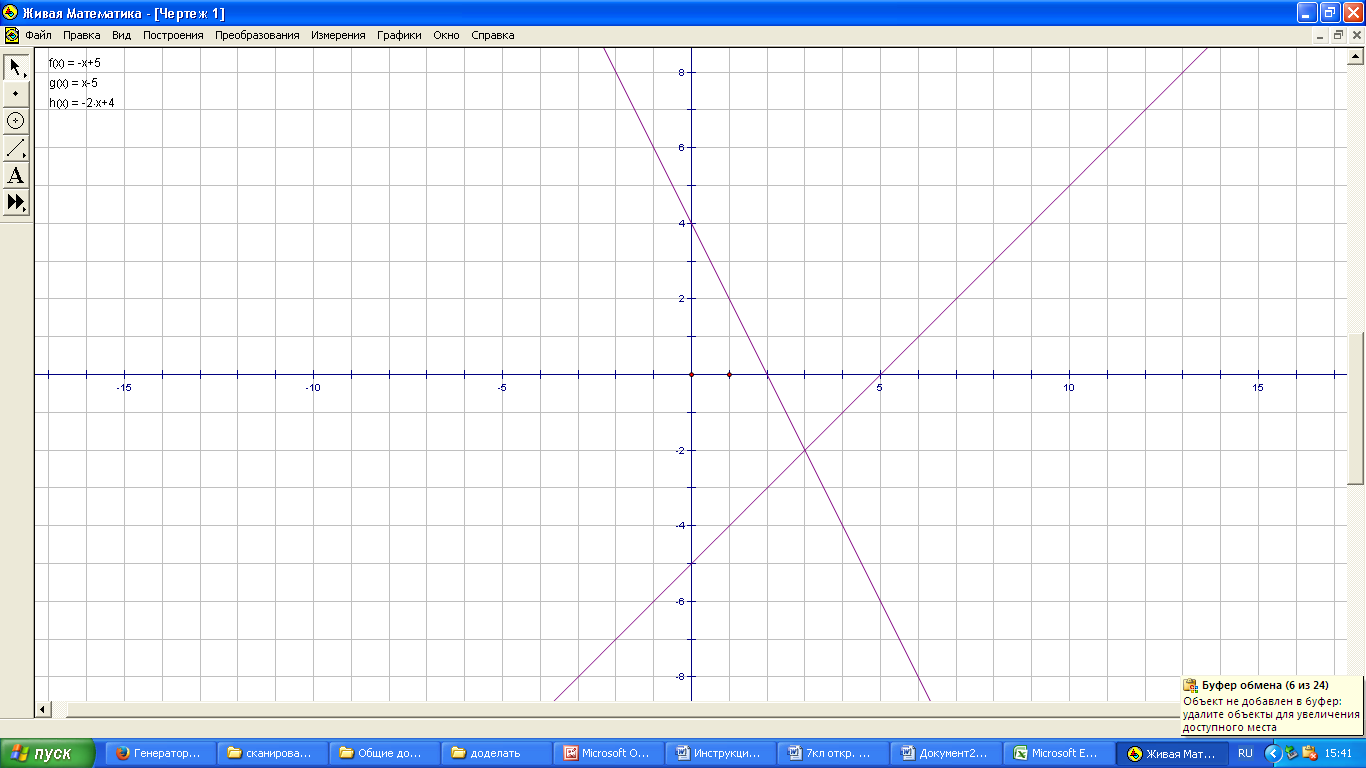
5. Определите графически, пересекаются ли графики функций у = —2х + 4 и у = х – 5 Решение:

составим таблицу значений для первого графика у = -2х + 4.

Х	-1	4
У	6	- 4

Составим таблицу значений для второго графика: у = х-5.

X	0	4
У	- 5	-1

Построим графики функций на одной координатной плоскости:

Графики пересекаются, точка пересечения имеет координаты (3; -2).

Ответ: (3; -2).

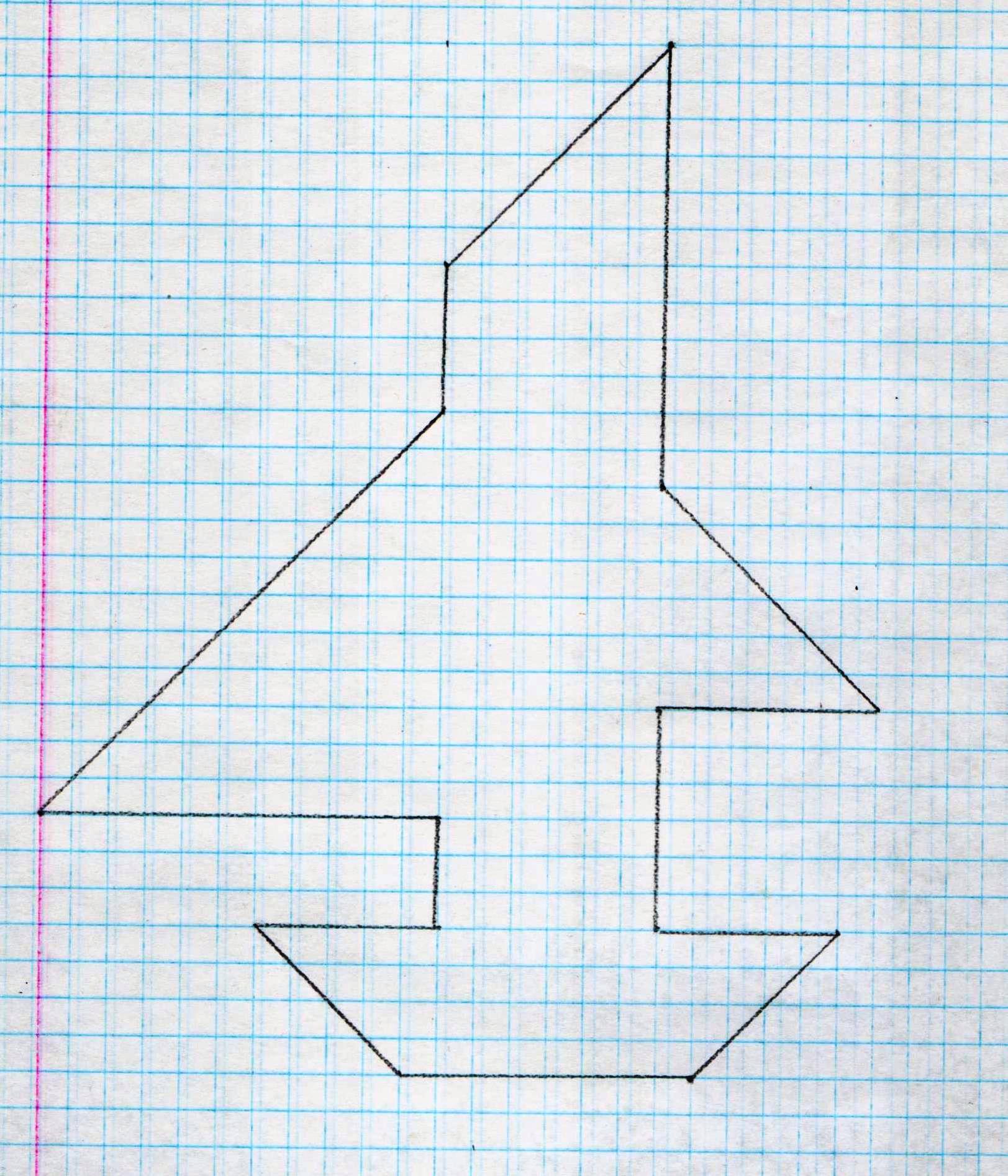
V. Выполнение заданий. Практическая работа (групповая)

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.

При построении графиков должны получиться контуры парусника.

VI. Подведение итогов.

VII. Домашнее задание: домашняя контрольная работа №2, выполнить номера 3,5,8 и доделать задание из V части.

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.

В одной системе координат построить графики функций.

1)у = х+16, 0 ≤ х ≤6;

2) х = 6, 10 ≤ у ≤ 22;

3) у = - х + 16, 6 ≤ х ≤ 12;

4) у = 4, 6 ≤ х ≤ 12;

5) х = 6, -2 ≤ у ≤ 4;

6) у = - 2, 6 ≤ х ≤ 11;

7) у = х – 13, 7 ≤ х ≤ 11;

8) у = - 6, - 1≤ х ≤ 7;

9) у = - х – 7, -5 ≤ х ≤ - 1;

10) у = - 2, -5 ≤ х ≤ 0;

11) х = 0, - 2 ≤ у ≤ 1;

12) у = 1, - 11 ≤ х ≤ 0;

13) у = х + 12, - 11 ≤ х ≤ 0;

14) х = 0, 12 ≤ у ≤ 16.