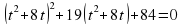| Сыныбы: 8 | |
| Сабақтың тақырыбы | Квадрат теңдеуге келтірілетін теңдеулер. Биквадрат теңдеулерге есептер шығару |
| Мақсаты | биквадрат теңдеу және квадрат теңдеуге келтірілген теңдеулерді шешуде жаңа айнымалы енгізу әдісімен шешу алгоритмін есептер шығаруда дұрыс қолдана алуға үйрене отырып, өтілген тақырып бойынша білімдерін тереңдетіп, жинақтау. |
| Күтілетін нәтиже | А. Биквадрат теңдеу және квадрат теңдеуге келтірілген теңдеулердің коэфиценттерін анықтайды. В. биквадрат теңдеу және квадрат теңдеуге келтірілген теңдеулердің шешуде жаңа айнымалы енгізу әдісімен шешу алгоритмін есептер шығаруда қолдана алуға үйренеді. С. Өтілген тақырып бойынша білімдерін тереңдетіп, жинақтайды.
|
| Әдіс- тәсілдер
| «Шатасқан баулар» стартегиясы, сәйкестендіру, деңгейлік тапсырма, тест, перфокартамен жұмыс, емтихан жинағынан тапсырмалар |
| Керекті жабдықтар | Оқулық Алгебра 8 сынып Ә. Н. Шыныбеков Алматы «Атамұра» 2012 Интербелсенді тақта, «Табыс» ағашы, алмалар, жапырақтар, бағалау парағы, |
| Сабақ барысы: |
| Сабақ кезеңдері | Мұғалім әрекеті | Оқушы әрекеті |
| Кіріспе 2 минут
3 минут: | Сыныпта ынтымақтастық атмосферасын қалыптастыру. Ұйымдастыру бөлімі: Амандасу, түгелдеу. Үй тапсырмасы «Ыстық орындық» әдісі арқылы тексеріледі. №189,190,191,192 жұптары №189,190,191,192 жұптары 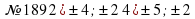
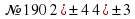
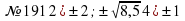
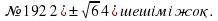
| Топ басшыларына бағалау критерийі беріледі.
Оқушылар үй жұмысын дәптерлерін алмаса отырып бірін бірі тексереді.
|
| Тұсаукесер 10 минут
| Мұғалім оқушыларға өткен тақырып бойынша сұрақтар қояды. Квадрат теңдеуді шешудің қандай әдіс-тәсілдері бар? Жауабы: Дискриминат, виет теоремасы, екімүшенің толық квадратын айыру, топтау тәсілі арқылы Жаңа айнымалы енгізу әдісін қарастырудың қандай қажеті бар? Жауабы: төртінші дәрежелі теідеулерді жаңа айнымалы енгізу арқылы квадрат теңдеуге келтіреміз. Квадрат теңдеуге келтірілетін теңдеулердің түбірлеріне неліктен тексеру жүргізу қажет? Жауабы: Тексеру арқылы шыққан мәндер берілген теңдеулердің түбірі болатынын анықтаймыз. Квадрат теңдеудің өмірде қайда қолданады? Вай-фай антенасын, теледидар антенасын жасауда, құрылыста, жерді өлшеуде қолданады?
«Шатасқан баулар» стратегиясы бойынша өткен тақырыптарды қайталау. (Мұғалім оқушыларға дұрыс және дұрыс емес тапсырмалар мен сұрақтар береді). Оқушылар жеке-жеке берілген тапсырманы оқып дұрыс емес тапсырманың қатесін тауып өз ойын тобында талқылап жауабын береді. (СТО,топтық талдау)
1-топтың тапсырмасы ах4+ bх2+с=0 бұл квадрат теңдеу. Квадрат теңдеудің дискрименанты нөлден үлкен болса екі түбірі бар. 5х4-6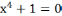 х2 +1=0 биквадрат теңдеудің коэффициентері a=5, b=-6, c=1. х2 +1=0 биквадрат теңдеудің коэффициентері a=5, b=-6, c=1. х2-7х+10=0 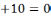 теңдеуінің түбірлерінің қосындысы х1+х2= 7, көбейтіндісі х1*х2=-10 тең. теңдеуінің түбірлерінің қосындысы х1+х2= 7, көбейтіндісі х1*х2=-10 тең. ах4+ bх2+с=0, a=0 теңдеуі биквадрат теңдеуі деп аталады. Мұндағы a, b, c белгілі тұрақты сандар ал х ізделінетің белгісіз. Бұндай теңдеуді шешу үшін х2=t алмастыруын еңгіземіз. 2-топтың тапсырмасы Биквадрат теңдеуді шешу үшін, теңдеуді at2+bt+c=0 түріндегі квадрат теңдеумен алмастырамыз. Квадрат теңдеуді шешіп t-ның мәнін t0 салыстырып. биквадрат теңдеуінің түбірлерін х2=t1 , х2=t2 теңдеуін шешу арқылы анықтаймыз. х2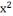 +3х4-4=0 бұл квадрат теңдеу,коэффициенттері a=1, b=3, c=-4. +3х4-4=0 бұл квадрат теңдеу,коэффициенттері a=1, b=3, c=-4. Биквадрат теңдеудің түбірлерінің ең көп шешімі екеу. Келтірілген квадрат теңдеудің түбірлердің қосындысы қарама-қарсы алынған екінші коэффициентке, көбейтіндісі бос мүшеге тең. x1 +x2 =-р, x1 x2= -q х4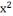 -20х2+64=0, х2=t, t2-20t+64=0, D=102-64=36, -20х2+64=0, х2=t, t2-20t+64=0, D=102-64=36, t= 10±6, t2=16 , t2=4, Жауабы:16; 4 3 топтын тапсырмасы 8х2+5х+10=0 Квадрат теңдеудің коэффиценттерін ата. а=8 в=5 с=10. 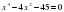 теңдеуінің түбірлері 5;7 теңдеуінің түбірлері 5;7
Берілген теңдеудегі өрнектің орнына жаңа айнымалыны еңгізіп, жаңа айнымалыға байланысты квадрат теңдеу алады. х2+8х+9=0 теңдеуінің түбірлері х1=9, х2= -1 Д=0 болғанда теңдеудің екі түбірі бар.
4 топтың тапсырмасы Биквадрат теңдеу формуласы ах4+ вх2+ с=0 9х4+17х2+8=0 биквадрат теңдеуінің коэфиценттері а=9 в=8 с=17 х4 + 8х2 – 9 = 0 теңдеуін шешейік х2 =у деп белгілейміз сонда у2+ 8у – 9 = 0 теңдеуін шешеміз D = 100 у1=1 , у2 = — 9 сәйкесінше х1,2 = ± 1 х2 ≠ — 9 Жауабы: ± 1 Дискриминант формуласы D = с2- 4ав Берілген төртінші дәрежелі теңдеуді шешу үшін жаңа t айнымалысын еңгіздік. Теңдеулерді шешудің мұндай әдісі жаңа айнымалыны еңгізу әдісі деп аталады. Ауызша есептер:
Сәйкестендіру арқылы биквадрат теңдеудің коэффициенттерін табу тапсырмасы беріледі.
| Топ басшылары бағалау парағын толтырып отырады.
Әр топ конверт тусин таңдайды. Әр конвертте тапсырмалар мен сұрақтарға жауап беру арқылы дұрыс дұрыс емес тапсырманың қатесін табады. Әр топ тапсырманы бірлесе орындап, бір оқушы тақтаға шығарады. |
| Негізгі бөлім | Жаңа айнымалыны еңгізу әдісінің алгоритмін еске түсіреміз. Теңдеудегі қандай да бір өрнекті жаңа айнымалы арқылы белгілеу; Берілген теңдеудегі өрнектің орнына жаңа айнымалыны еңгізіп, жаңа айнымалыға байланысты квадрат теңдеу алу; Шыққан квадрат теңдеуді шешу; Алмастыру арқылы алғашқы айнымалының мәнін табу; 5. Табылған түбірлерге тексеру жүргізіп, берілген теңдеудің түбірлерін анықтау; | Оқушылар жаңа айнымалыны еңгізу әдісінің алгоритмін еске түсіреді.
|
|
| Оқулықпен жұмыс 193,195
А деңгей 1 балл Теңдеуді шешіңдер 4a 33 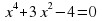 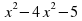 В деңгей 2 балл 4b 35 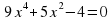 2 2 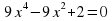 С деңгей 3 балл 4с 54 А) 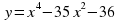 функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар. функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар. В) 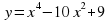 функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар. функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар.
Сергіту сәті Мақал-мәтелдер беріледі. Оның ішіндегі екі сан есім квадрат теңдеудің түбірлері, яғни Виет теоремасына кері теорема бойынша квадрат теңдеу құрастыру керек. Ер бір рет өледі, қорқақ мың рет өледі. Ж: 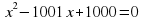 Жігіт бір сырлы, сегіз қырлы. Ж: 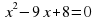 Ұлға отыз үйден, қызға қырық үйден тыю. Ж: 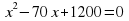 Жеті жұрттың тілін біл, (жеті түрлі білім іл) 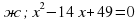
| Оқулықпен жұмыстану кезінде топта оқушылар топта ақылдаса отырып шығарады. Әр топтан бір оқушы тақтаға шығарады.
Оқушылар есепті жеке шығарып болған соң дәптерлерімен көршілерімен алмастыра отырып, интербелсенді тақтамен тексереді. |
| Қорытынды | Өзіндік жұмыс Теңдеуді шешіңдер 2х4 – 4х2 + 5 = 0 А) 1; 4 В) түбірі жоқ С) 5; 2 Д) 3; 2 х4 – 7х2 + 12 = 0 А) ± 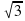 ; ± 2 В) ø ; ± 2 В) ø С) түбірі жоқ Д) ± 4; ± 3 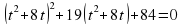 А) -6.-2; -7.-1 В) ø С) -7.-1 ; Д) -6.-2 | Оқушылар биквадрат теңдеуде жаңа айнымалы енгізу а арқылы квадрат теңдеу құрады.
• . |
| Бағалау
Рефлексия | Үйге тапсырма: № 194,196 жұптары
«Табыс» ағашын отырғызайық. Жасыл желек-сыныбымыздағы көңіл-күй, ал ағаш жемістері-сіздердің білімдеріңіз. Жасыл алма: маған сабақ ұнады, тақырыпты меңгердім. Сары алма: Тақырыпты түсіндім, бірақ есептеген кезде қиналдым. Қызыл алма: сабақ маған түсініксіз.
| Топ басшылары өз бағалау парағы бойынша бағаларын талдап айтады.
Оқушылар алмаларын, жапырақтарын терекке жапсырады. |
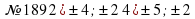
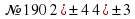
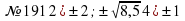
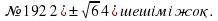
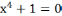 х2 +1=0 биквадрат теңдеудің коэффициентері a=5, b=-6, c=1.
х2 +1=0 биквадрат теңдеудің коэффициентері a=5, b=-6, c=1.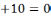 теңдеуінің түбірлерінің қосындысы х1+х2= 7, көбейтіндісі х1*х2=-10 тең.
теңдеуінің түбірлерінің қосындысы х1+х2= 7, көбейтіндісі х1*х2=-10 тең.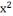 +3х4-4=0 бұл квадрат теңдеу,коэффициенттері a=1, b=3, c=-4.
+3х4-4=0 бұл квадрат теңдеу,коэффициенттері a=1, b=3, c=-4.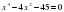 теңдеуінің түбірлері 5;7
теңдеуінің түбірлері 5;7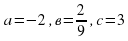
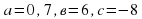
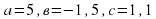
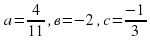
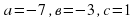
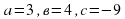
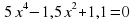
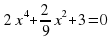
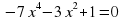
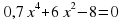
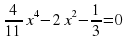
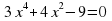
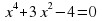
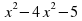
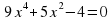 2
2 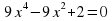
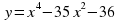 функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар.
функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар.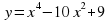 функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар.
функциясы графигін абсцисса осімен қиылысу нүктелерінің координаталарын табыңдар.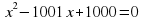
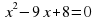
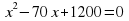
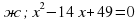
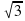 ; ± 2 В) ø
; ± 2 В) ø