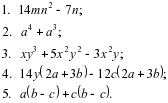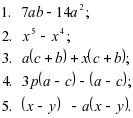| Добрый день, ребята. -Давайте вспомним, о чём мы говорили, чем занимались, что прошли на прошлом уроке? (Ответы детей) - Чем мы сегодня будем заниматься, как вы думаете? Откройте тетради, запишите число, классная работа и тему урока: «Вынесение общего множителя за скобки» Слайд 1 Девиз нашего урока «Мало иметь хороший ум, главное – хорошо его применять». Сегодня нам как раз нужно как можно более эффективно применять свойства нашего ума при решении примеров и заданий. Слайд 2
|
Ответ. На прошлом уроке мы изучали новую тему: «Вынесение общего множителя за скобки, решали задания по данной теме»
Ответ: Закрепим умения вынесения общего множителя за скобки путем разложения многочлена на множители способом. Записывают число, классная работа и тему урока в тетради: «Вынесение общего множителя за скобки»
|
| 2.Проверка домашнего задания (3 мин) Есть вопросы по домашнему заданию? если нет посмотрите, проверьте свои решения и ответы. Слайд 3 №667 (в,г), №674 (а), №676, 674 (б). Да доске №667 (в,г) Представьте в виде произведении: В) 4х4+8х3 -2х2 = 2х2* (2х2+4х-1) Г) 5а - 5х2- 10х4= 5а*(1-а-2а2)
№674 (б) Решите уравнение: + = 2 Умножим обе части уравнения на 9 21 – 4х – 24х -45 =18 28х = 21 - 45 -18 28х = - 42 х= -1,5 Ответ: х= -1,5
№676 Запишите в виде выражения: а) произведение разности а и b и их суммы ( а+b)* (а- b)
б) сумму квадратов а и b а2 + b2
в) квадрат суммы а и b ( а+b)2
г) квадрат разности b и с ( b - с)2
д) куб разности b и с
( b - с)3
Е) сумму кубов b и с
а3 + b3
Мы с вами сегодня посетим виртуальный «Музея науки и техники». Но для того, что бы нам в него попасть нам нужно получить билеты, для этого поработаем устно.
| Проверяют Д/З, исправляют ошибки, если есть. |
| 3.Актуализация прежних знаний. (5-7 мин) Представьте произведение в виде степени, найдите правильный ответ к данному произведению: (слайд 4)
1.х3 х3 = х9
2. а6 а2а4 = а12
3. х3 х = х4
4. 26 * 24 = 210 20 х6
Найдите общий множитель одночленов: Слайд 5
а) х3; - х; х4; х в) – а3; а5; а; а б) 7ab3; - 14ab; 28сb2; 7b г) - 3xу2; - 18ау6; 6су; 3у
1)Какая из схем поясняет, как можно вынести общий множитель за скобки? Слайд 6 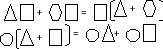
2.Скажите, пожалуйста, какое свойство напоминает нам вторая схема. 3.А какое правило мы можем сформулировать глядя на 2-ю схему? 4. Разложите многочлен на множители: Слайд 7
1. Что значит разложить многочлен на множители? 6а2b + 15b2 = 3b*2a2 + 3b * 5b = 3b* (2а2 + 5b)
Какой способ разложения многочлена на множители мы применили?
4. Закрепление. Обобщение и систематизация. (25 мин) Отлично в музей мы попали. И перед нами картинная галерея. На доске фамилии ученых – математиков.
Возле каждой фамилии подписаны числовые выражения.
Ваша задача: выполнить действия и по полученным ответам догадаться, о каком ученом шла речь в моем тексте. Кто желает пойти к доске? Один работает у доски, остальные работают в тетрадях. Слайд 8 Архимед Пифагор Евклид Декарт Галуа – 4b – 5аb (х – у) – 5а2b2 4b Этот античный ученый побеждал на Олимпийских играх и впервые открыл математическую теорию музыки. (Пифагор)
5b*(2b2 – a) = 10b3 …- 5аb Слайд 9 Каким правилом мы здесь воспользовались?
Ученый, который, несмотря на свою молодость, успел сделать много открытий в математике, но, к сожалению, был убит на дуэли в 21 год (Галуа)
– 3аb – 12b2 = – 3b (а + …4b); Слайд 10 Какой вы применили здесь способ? (Слайд 10) Его любимая фраза – «что и требовалось доказать» (Евклид) 3а(х – у) + 2b (х – у) = ( х-у) …. *(3а + 2b) Евклид Слайд 11
А, что мы сделали в задании?
| Активно работают в устной работе
х3 х3 = х6 а6 а2а4 = а12 х3 х = х4 26 * 24 = 210
1.Первая схема поясняет вынесение общего множителя за скобки, т.к. в этой схеме есть общий множитель квадрат 2. Распределительное свойство. 3. Правило умножения одночлена на многочлен? (Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить)
4. 1.Представление многочлена в виде произведения двух или нескольких многочленов называют разложением многочлена на множители.
Вынесение общего множителя за скобки.
Записывают решение в тетради. 5b(2b2 – a) = 5b*2b2 +5b*(-а) = =10b3 - 5аb Ответ: Умножение одночлена на многочлен.
– 3аb – 12b2 = -3b*а - 3b* 4b = – 3b (а +4b); Ответ: Вынесение общего множителя за скобки.
3а(х – у) + 2b (х – у) = (3а + 2b) *(х – у) Ответ: Разложили многочлен на множители?
|
|
А теперь мы отправимся в зал инструментов. (6 мин) Сейчас вас ждет парная работа. Не забывайте правила при работе в парах. Внимательно прочитайте задание. 2. Если ты выполняешь задание с товарищем, который приблизительно равен тебе по силам, то старайтесь разделить всю работу поровну. Помогайте друг другу в случае затруднений, тактично исправляйте ошибки друг друга. 3. Если твой товарищ справляется лучше тебя, не стесняйся обратиться к нему за помощью, попросить что-то объяснить. Но не злоупотребляй этим. Не обижайся на товарища, если он исправит ту или иную ошибку. 4. Если ты видишь, что твой товарищ справляется хуже тебя, помоги ему, однако старайся делать это так, чтобы он сам работал с полным напряжением сил. Следи за тем, не делает ли он ошибок, если делает, то тактично и доброжелательно исправляй их. 5. Запомни главное правило: в любом коллективном деле нужна согласованность действий и готовность помочь своему товарищу. Ты в ответе за него. Он – за тебя.
Ваша задача - упростить выражение и ответить на предложенный вопросы. Карточки с вопросами на столе.
(на доске) инструмент: х2(а – в) + у2(а – в) инструмент: 4а2в2 + 8а2в3 +6ав4 инструмент: 5(х – 3) – а(3 – х)
Циркуль Абак Циркуль, линейка. (х – 3)(5 + а) (а – в)(х2 + у2 ) 2ав2 (2а + 4ав + 3в2)
Карточка с вопросами. 1. Назовите древний геометрический инструмент, который, по утверждению римского поэта Овидия (Iв.), был изобретен в Древней Греции. (циркуль) 2.Летописец сообщает, что строительство Успенского собора в Кремле велось в «кружало и в правило». К помощи каких инструментов прибегали мастера? (к циркулю и линейке) 3. Это устройство применялось для арифметических вычислений в древности (абак).
Один ученик из пары выходит к доске и комментирует свой ответ. | Парная работа с записью в тетради. Упростить выражение
4а2в2 + 8а2в3 +6ав4 = 2ав2*2а + 2ав2* 4ав + 2ав2 * 3в2 = 2ав2*(2а + 4ав + 3в2) Циркуль и линейка
х2(а – в) + у2(а – в) = (х2 + у2)* (а – в) Абак
5(х – 3) – а(х - 3) = (5 –а)* (х – 3) Циркуль |
| Давайте посмотрим экспонат в музее посвященный превращениям квадратного листа бумаги. (10 мин) Японская мудрость издревле гласит: «Великий квадрат не имеет пределов». Попробуй простую фигурку сложить, И вмиг увлечет интересное дело Как называется это искусство? Закончите разложение на множители в данном многочлене. Найдите недостающее слагаемое и сложите зашифрованное слово из ответов в таблице. Под каждой буквой находится свой ответ:
| А | Г | И | М | О | Р | | 2с | 4с2 | 5ас | 4ас2 | 3с2 | 3ас |
4а3с2 + 36а2с3 + 6ас4 = 2ас2(2а2 + 18ас + …) 2а2с4 – 2а4с2 +6а3с3 = 2а2с2(с2 – а2 +…) 20а3с2 + 4а2с = 4а2с (… + 1) 28а2с4 – 21а3с2 = 7а2с2(…– 3а) 5) 15а4с3 – 5а2с2 + 10а2с2 = 5а2с(3а2с2 – с + …) 6) 21а3с2 + 28а2с3 – 14ас = 7ас(3а2с + … – 2) 7) 12а3с4 – 20а3с2 + 4а2с =4а2с(3ас3 – … + 1)
Ребята, мы побывали в музеи, а теперь пришло время проверить наши знания. Я раздам каждому карточки с заданиями.
Ваша задача: вынесите общий множитель за скобки, выполняете решение и вписываете ответ в карточку. (5 мин) 1 вариант
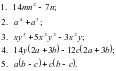 2 вариант 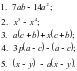
Критерий оценивания самостоятельной работы (на доске) заданий – «5»; задания – «4»; 3 задания – «3»; менее 3-х заданий – «2»
А теперь взяли в руки карандаши и глядя на доску с ответами выполнили проверку. Открыли дневники и поставили себе оценки. Дневники отложили в сторонку.
Подведение итогов урока: Анализ деятельности.
Ребята, мы достигли поставленной цели? Какие были трудности? Что было интересно? У вас у каждого на столе лежат смайлики. Дорисуйте, пожалуйста ему свое настроение.
 
Понравился урок. Я тему так и не усвоил, урок не понравился

Я равнодушным остался к уроку. А теперь покажите мне свое настроение? Вложите их себе в дневники.
Домашнее задание. ( 2 мин) П. 28. № 667 (а,б),№672 (а–в), №669 (в,г)
Ребята урок окончен, спасибо за работу на уроке! Решение Д.З. № 667 (а,б) Представьте в виде произведения: с3 – с4 + 2с5 = с3(1 – с + 2c2) 5m4 – m3 + 2m2= m2(5m2 – m + 2) №672 (а-в) Разложите на множители: 8m*(a – 3) + n*(a – 3) = (8m + n) * (a – 3); (р2 – 5) – q*(р2 – 5) = (р2 – 5)*(1 – q) №669 (в,г) Разложите на множители многочлен: в) 3ax – 6ax2 – 9a2x =3ax(1 – 2x – 3a) г) 8a4b3 – 12a2b4 +16a3b2 = 4a2b2(2a2b - 3a2 + 4a) | Решение у доски и с записью в тетрадях. 1) 4а3с2 + 36а2с3 + 6ас4 = 2ас2 * 2а2 + 2ас2*18ас +2ас2 * 3с2 = 2ас2(2а2 + 18ас + 3с2) о 2) 2а2с4 – 2а4с2 +6а3с3 = 2а2с2 * с2 - 2а2с2 * а2 + 2а2с2 * 3ас = 2а2с2(с2 – а2 +3ас) Р 3) 20а3с2 + 4а2с = 4а2с * 5ас + 4а2с *1= 4а2с (5ас + 1) И 4) 28а2с4 – 21а3с2 = 7а2с2* 4с2 - 7а2с2* 3а = 7а2с2(4с2– 3а) Г 5) 15а4с3 – 5а2с2 + 10а2с2 = 5а2с *3а2с2 - 5а2с* с + 5а2с *2с =5а2с(3а2с2 – с + 2с)А 6)21а3с2 + 28а2с3 – 14ас = 7ас * 3а2с + + 7ас *4ас2 - 7ас *2 = 7ас(3а2с +4ас2 – -2) М 7) 12а3с4 – 20а3с2 + 4а2с = 4а2с *3ас3 – - 4а2с * 5ас + 4а2с * 1 =4а2с(3ас3 – 5ас + 1) И ОРИГАМИ
Решение самостоятельной работы учащиеся выполняют на карточках.
1 вариант. 1) 14mn2 – 7n=7n * (7mn -1); 2) a4+ a3 = a3 *(a – 1) 3) xy3 + 5x2y2 – 3x2y = xy*( y2 + 5 xy – 3x) 4) 14y(2a + 3b) – 12с(2a +3b) = (14y -12c) – (2a + 3b) 5) a(b- c) + c(b-c) = (a + c)* ( b – c)
2 вариант 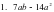 = 7a(b – 14 a) = 7a(b – 14 a)
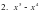 = x4(x – 1) = x4(x – 1)
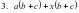 = (a + x) *( b + c) = (a + x) *( b + c)
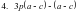 = ( 3p - 1)*( a – c) = ( 3p - 1)*( a – c)
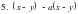 = ( 1 – a)*( x – y) = ( 1 – a)*( x – y)
Выполняют самопроверку.
Отвечают на вопросы.
Работают со смайликами.
Записывают домашнее задание. П. 28. № 667 (а,б),№672 (а–в), №669 (в,г)
|
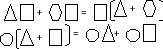
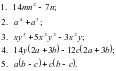
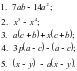


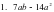 = 7a(b – 14 a)
= 7a(b – 14 a)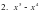 = x4(x – 1)
= x4(x – 1)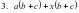 = (a + x) *( b + c)
= (a + x) *( b + c)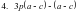 = ( 3p - 1)*( a – c)
= ( 3p - 1)*( a – c)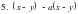 = ( 1 – a)*( x – y)
= ( 1 – a)*( x – y)