Актуализация знаний Учитель подходит к доске, на развороте доски написаны задания. - У меня на доске написаны задания. Кто знает, как решать, поднимайте руки, я увижу. Ребята говорят решение, учитель записывает решение на доске.
-Молодцы, все сделали верно. В начале урока мы вспоминали одно свойство чисел, какое? Это свойство называется распределительным свойством чисел. Теперь давайте откроем тетради, подпишем число, сегодня пятое марта, классная работа, тему урока.
Запишем распределительное свойство на буквах, вы в тетрадках, я запишу на доске, диктуйте, как запишем. Запишем это свойство наоборот. Этим свойством мы воспользуемся при иизучении новой темы. | 1 задание под буквой а): Здесь 3,5 по свойству перед скобками, а в скобках будет 6,8+3,2 и получится 35; под буквой b): Тут тоже 12,4 пишем за скобкой, в скобках 14,3-4,3, и получается 124. 2 задание под а): Мы 12 умножаем на 10, ставим знак «-» и 12 умножаем на 3b, получилось 120-36b; под b): 5 умножаем на 12a, ставим знак «-», 5 умножаем на 2b и получаем 60a-10 b. 3 задание под а): Ставим 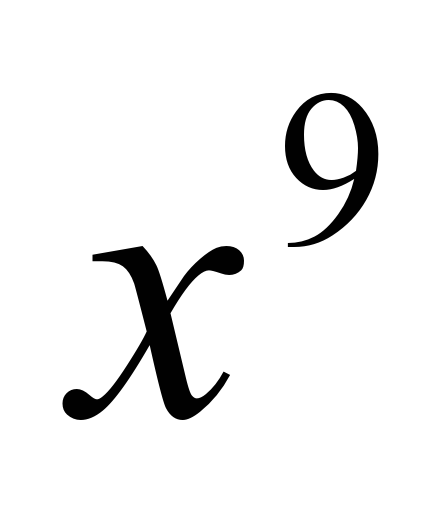 ,т.к. чтобы найти (*) нужно ,т.к. чтобы найти (*) нужно 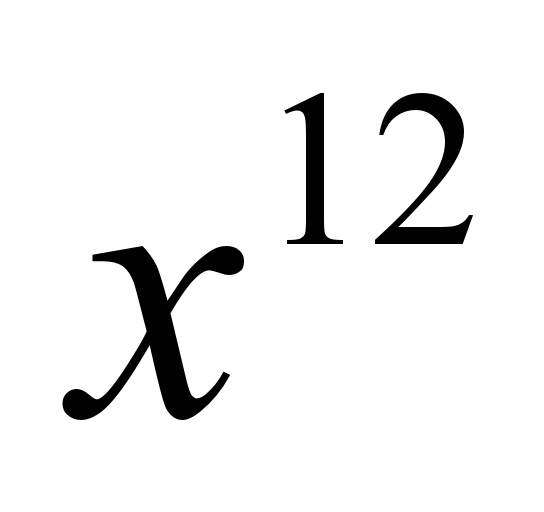 разделить на разделить на 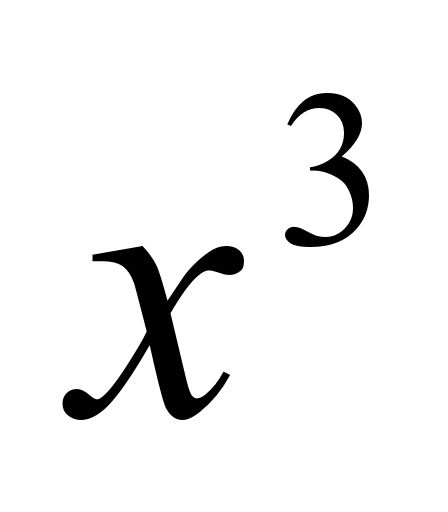 , основание оставляем тем же, а показатели вычитаем, получаем , основание оставляем тем же, а показатели вычитаем, получаем 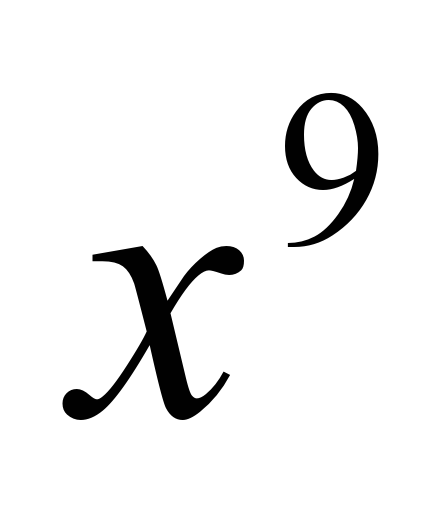 ; ; под b): Ответ 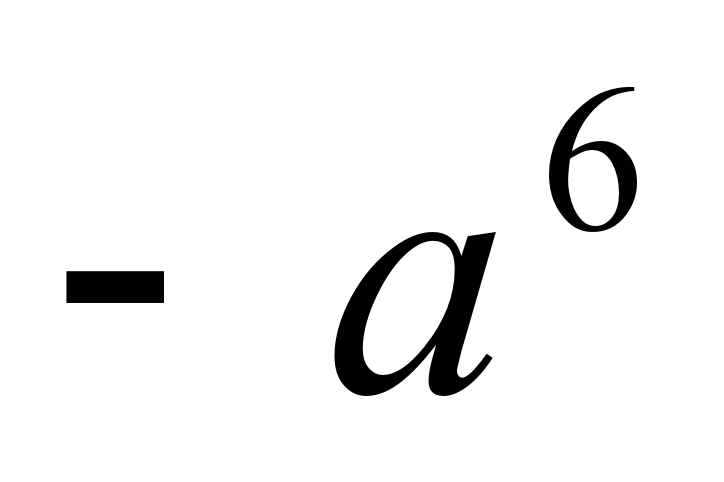 , т.к. если мы , т.к. если мы 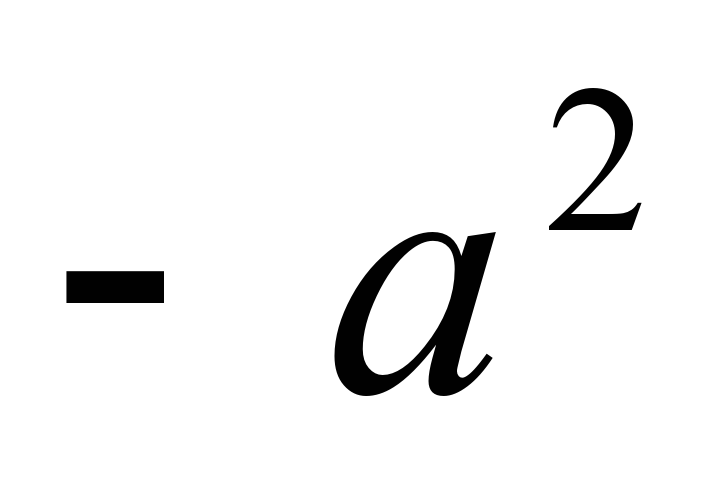 умножим на умножим на  , получим , получим 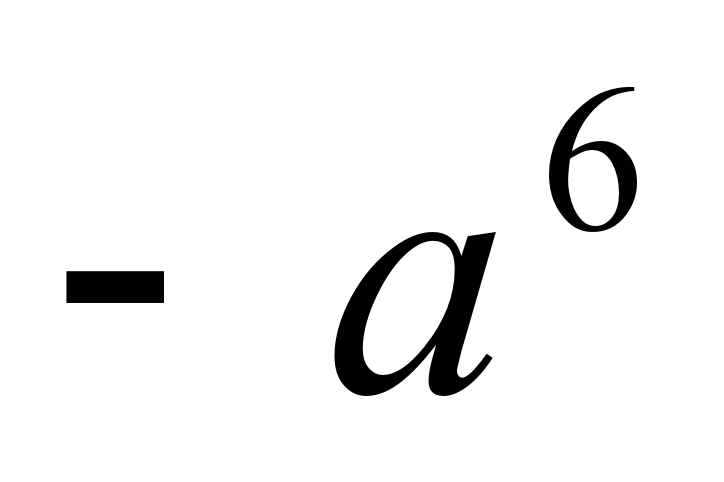 . .
4 задание: Под а) степень равна семи, т.е. мы должны сложить все степени одночлена Под b) степень равна шести Под с) степень равна нулю.
распределительное.
умножить в скобках b плюс c равно а умножить на b плюс а умножить на с. | Найдите значение выражения: 3,5*6,8+3,5*3,2 12,4*14,3-12,4*4,3 Раскройте скобки: 12*(10-3b) (12a-2b)*5 Какие одночлены следует поставить вместо (*), чтобы получилось тождество: 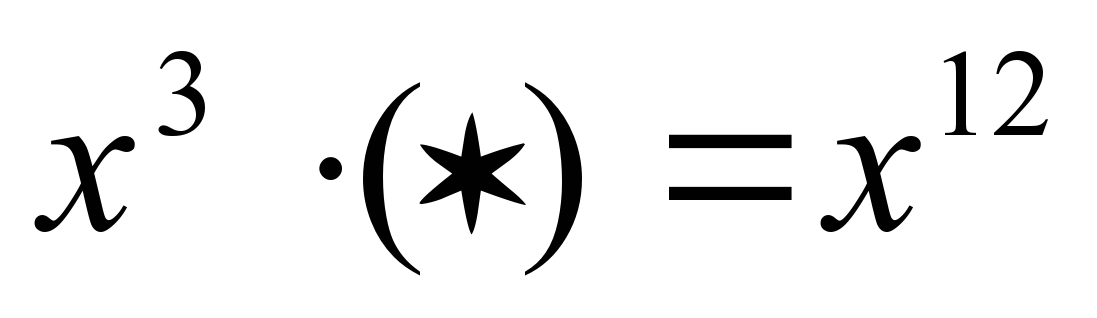
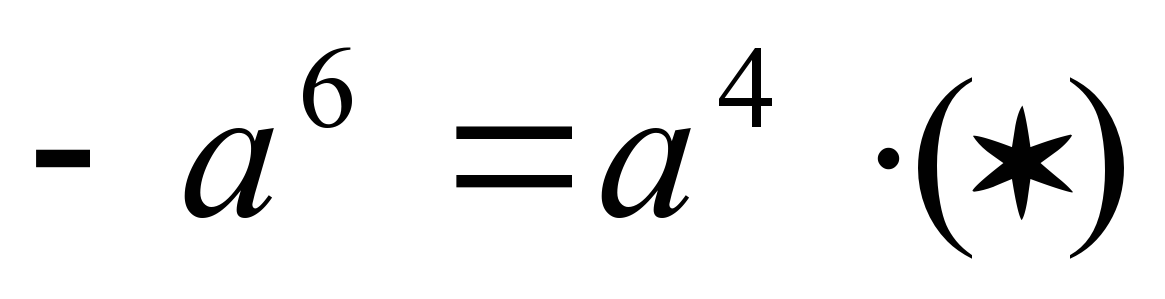
Какова степень одночлена? 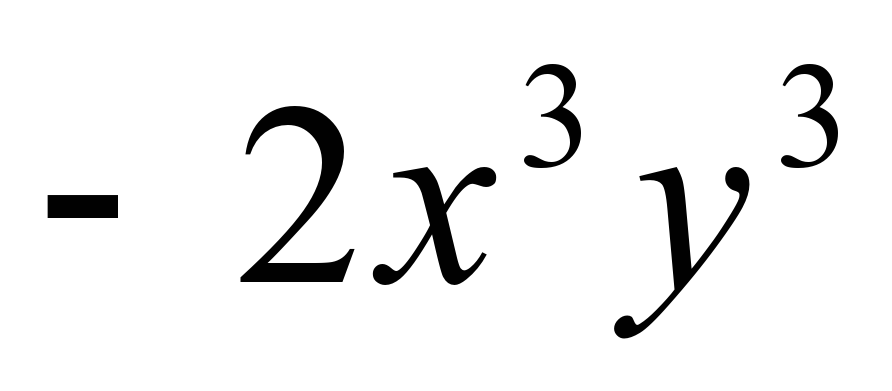
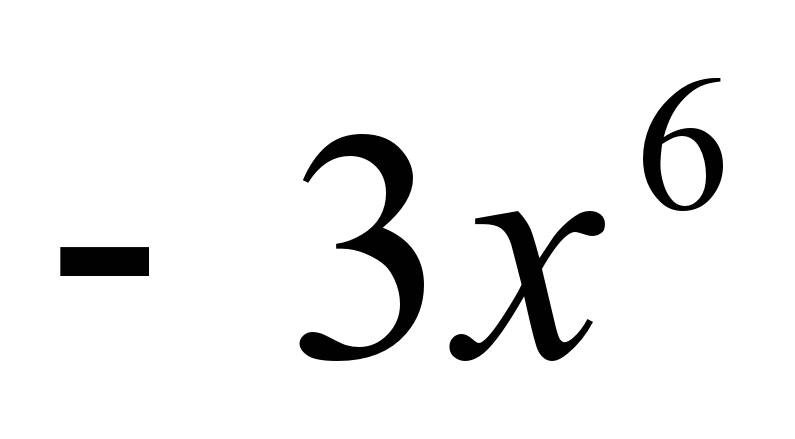
71
Открывается центральный разворот доски, справа подписано число 5.03 В центре доски название темы урока: Вынесение общего множителя за скобки.
a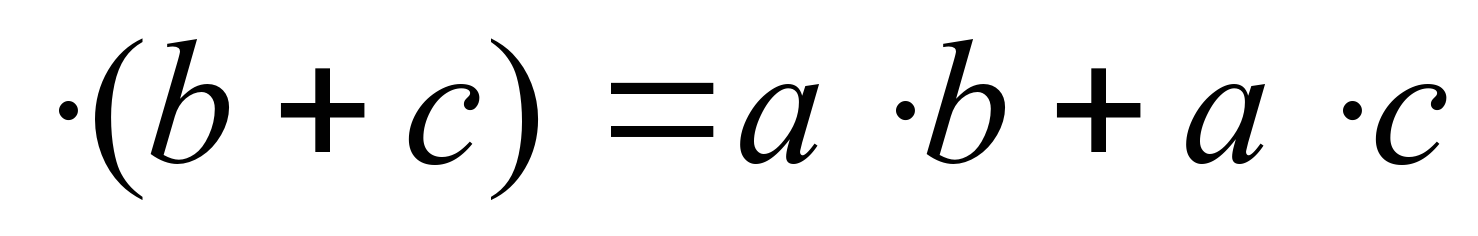
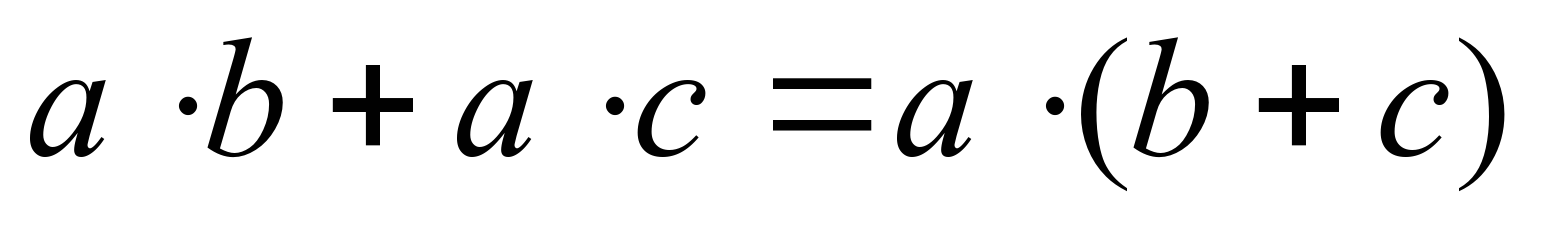
|
Введение нового материала Учитель объясняет: При решении различных уравнений полезно иногда заменить многочлен произведением нескольких многочленов. Представление многочлена в виде произведения нескольких многочленов называется разложением многочлена на множители. Сегодня на уроке мы познакомимся с одним из способов разложения многочлена на множители – вынесением общего множителя за скобки. У меня на доске записан пример. Послушайте задание: вынесите общий множитель за скобки. Можем ли мы выполнить такое задание? Тогда давайте будем выполнять задание вместе. Скажите мне, а как можно представить число 15 в виде произведения двух чисел? Правильно, а как можем представить 10? Давайте запишем, что у нас получилось А есть ли у нас что-нибудь одинаковое в первом и втором одночленах? Подчеркнём её карандашом А ещё есть что-нибудь одинаковое?
Да, букву а мы тоже подчеркнем и перепишем что получилось по другому – то, что подчеркнули перенесем на первое место. Посмотрите внимательно на доску, записанное вам начего не напоминает?
Ребята, то, что мы с вами сейчас проделали называется вынесением общего множителя за скобки. Общим множителем у нас является выражение 5а |
Нет, мы не умеем такого делать.
15 это 3 умножить на 5 10 это 2 умножить на 5
пятерки
Класс: нет есть ещё буква а
Можно записать с помощью распределительного свойства; 5а за скобку, в скобках остается 3b+2.
|
15ab+10a=
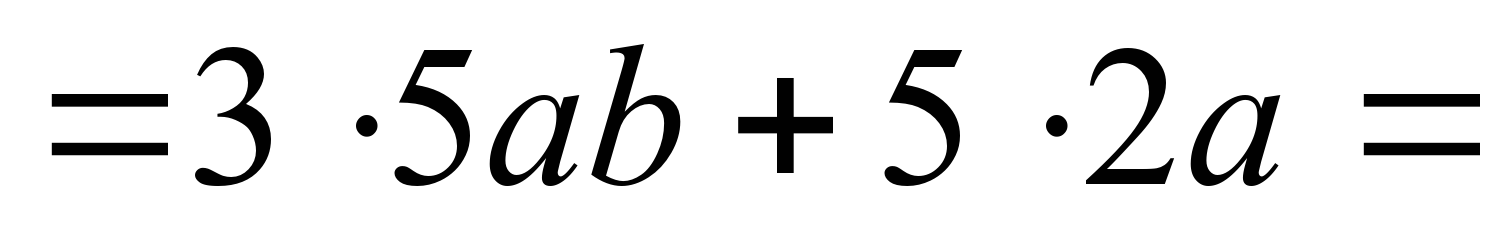
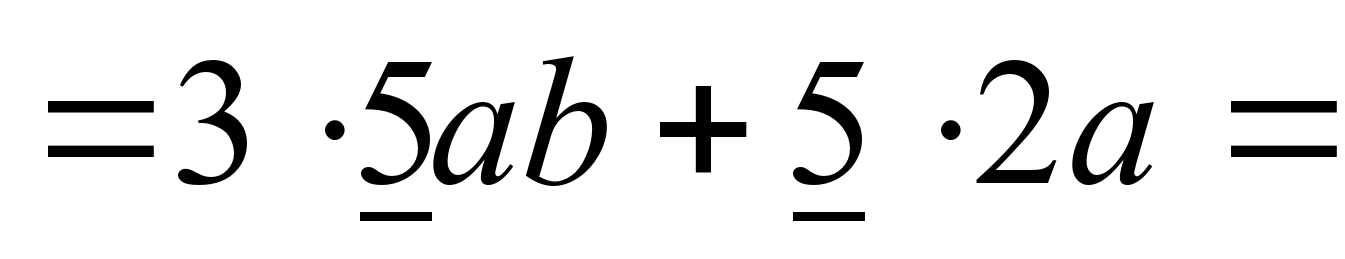
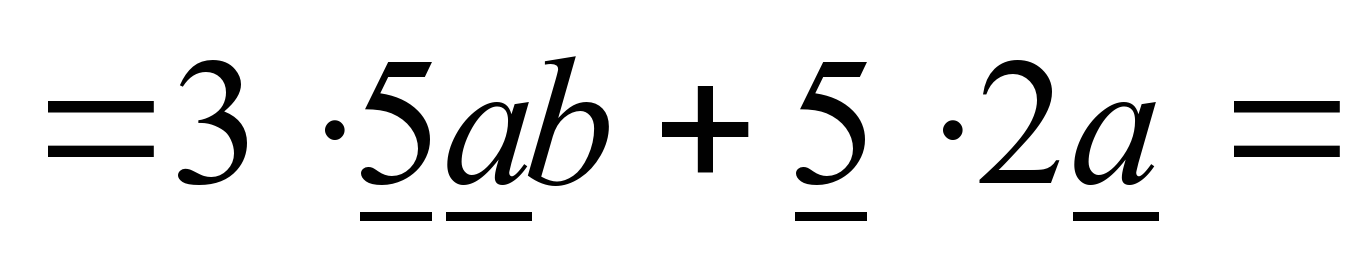 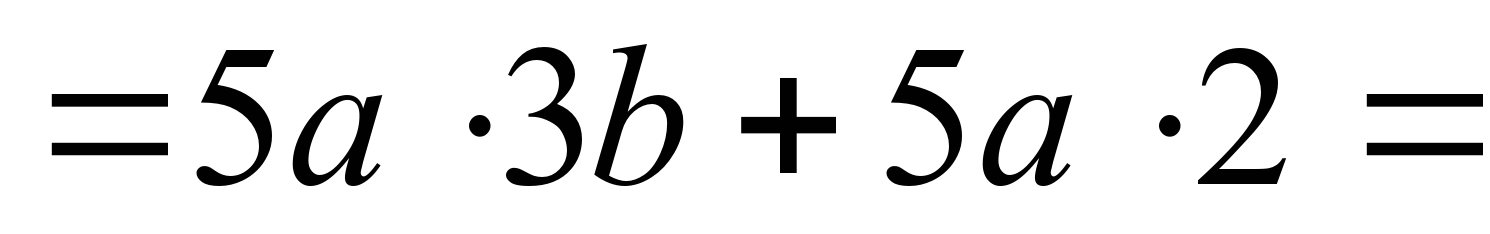
=5а(3b+2).
|
Закрепление нового материала Теперь давайте порешаем номера на закрепление, они написаны на доске. Заданий много, поэтому сегодня все из вас порешают у доски. Начнем с номера 654 и выходим к доске по порядку с первой парты. Наташа, прочитай задание
Что мы сначала будем делать?
Ребята, если вы сразу находите множители, то можете их не подчеркивать. Ребята, обратите внимание, у нас вначале был двучлен и после вынесения в скобках остался тоже двучлен. Как можно проверить, правильно ли мы вынесли множитель? Раскройте, посмотрим, что получиться Значит решили верно. Теперь решаем под б)
Учитель в это время проходит по классу, смотрит, кто как решает, заглядывает в тетрадки к учащимся и одновременно наблюдает за тем, что происходит на доске и если нужно, исправляет ошибки. -Класс, вы согласны с решением? Решаем дальше. В этом примере можно выносить как –а, так и а. Что будем выносить? Класс, все согласны с тем, что получилось? Давайте проверим. Раскроем скобки.
Запомните, если мы выносим знак «-», знаки в скобках меняются. Что тогда получим? Давайте раскроем скобки. Получилось верно.
У доски решает ученик.
Можно вынести и просто а. А кто вынес просто а, что у вас получилось в скобках?
Начинаем № 657 два первых столбика.
Смотрим, какие цифры одинаковые у первого и второго одночленов? А буквы есть одинаковые? Выносим и числовый и буквенный общий множитель. Кому трудно, одинаковые множители подчеркивайте. Решаем по б) Скажите, какое наименьшее общее кратное у чисел 3 и 6? Наименьшее общее кратное это такое число, на которое делится и 3 и 6 без остатка. На что делится 3 и 6 без остатка? Верно. Тройку мы и выносим. А ещё что можно вынести?
Значит выносим 3b. Верно, решаем под в)
Да. Выносите. Вынесли 5n, что же осталось от второго множителя? Помните мы с вами говорили, что если у нас был двучлен, то и в скобках должен остаться тоже двучлен. От первого множителя остался минус m, от второго останется единица, запомните это. А кто вынес другой множитель?
Под буквой д) решим.
На какое наименьшее число делятся 5 и 15 без остатка? У нас есть 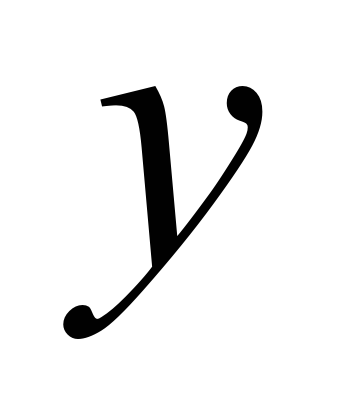 и и 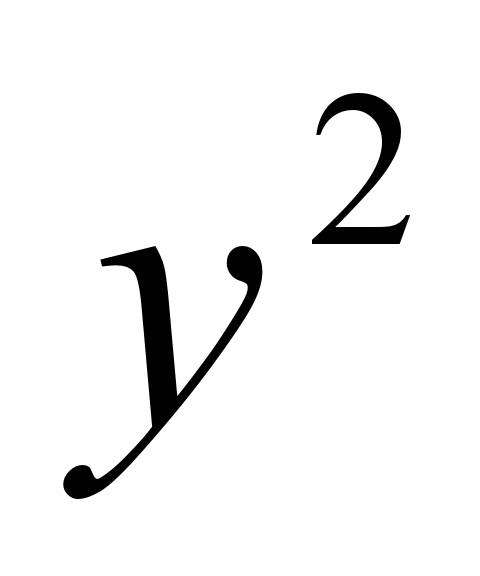 . Какой из этих показателей наименьший? . Какой из этих показателей наименьший? Выносим тот множитель, у которого показатель наименьший.
Учитель все время проходит по классу, подходит к ученикам, если что-то непонятно – то объясняет, тем самым осуществляет контроль за учениками. -Решаем дальше.
Верно, не забывайте про единицу. Класс, сверяйтесь, у всех так получилось?
Решать у доски выходит ученик..
И последний пример.
Сначала мы выносим числовой множитель. Какой множитель можно вынести? Теперь выносим тот буквенный множитель, показатель степени которой наименьший. И что получается? Сережа, а как можно проверить правильно ли мы вынесли множитель?
Значит вынесли множитель верно.
Ещё один номер начнем, № 658. Прочитайте задание. Ученик решает у доски.
Не забывайте про единицу, её мы никуда не теряем.
Верно, класс сверяйтесь, особенно те, кто решает вперед. |
К доске выходит ученик. Разложите на множители и сделайте проверку. а) mx+my= найдем одинаковые множители, это m и m, подчеркнем их. Вынесем m за скобки, в скобках остается x+y.
можно раскрыть скобки
m умножить на x плюс m умножить на y
б) kx-px. Здесь общий множитель х. Его можно вынести зи скобки. В скобках остается k-p.
Да
в) –ab+ac= -а будем выносить. В скобках останется b+c Все: Да -а умноженное на b минус a умноженное на c у нас неверно. Нужно, чтобы в скобках стоял знак минус.
-а умноженное на скобку, в скобках b минус c. г) –ma-na Выносим общий множитель за скобки, это минус а. В скобках остается m+n. У меня получилось а умноженное на скобку, в скобках минус m минус n.
а) 7ах+7bx. Семерки.
Да, х. Выносим 7х. В скобках остается а плюс b.
б) 3by-6b.
На 3.
b
остается в скобках y-2. в) -5mn+5n выносим 5 за скобки, получаем –mn+n в скобках Можно вынести ещё и n. Ноль.
Выносим -5n, в скобках получилось m-1.
д) 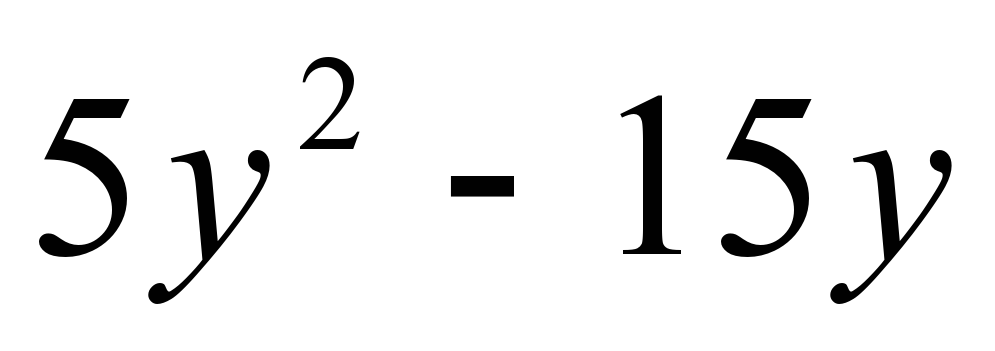 на 5
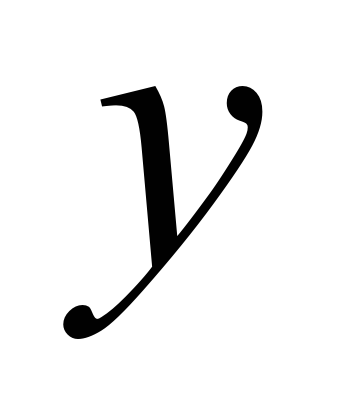
Значит выносим 5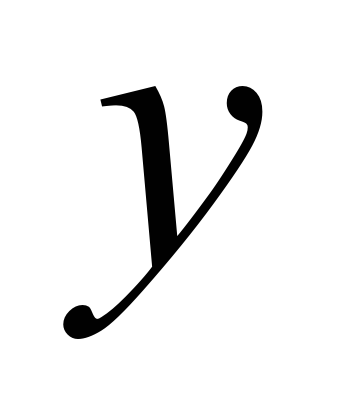 . . В скобках остается от первого множителя 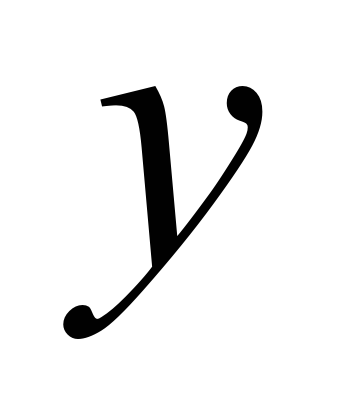 , от второго минус 3 , от второго минус 3
е) 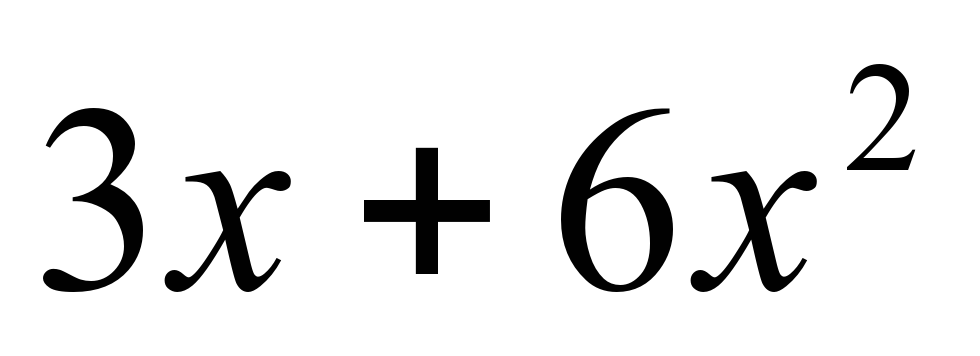 можно вынести 3х, получается 3х умноженное на скобку, в скобках от первого множителя остается единица, от второго 2х. Класс: Да. ж) 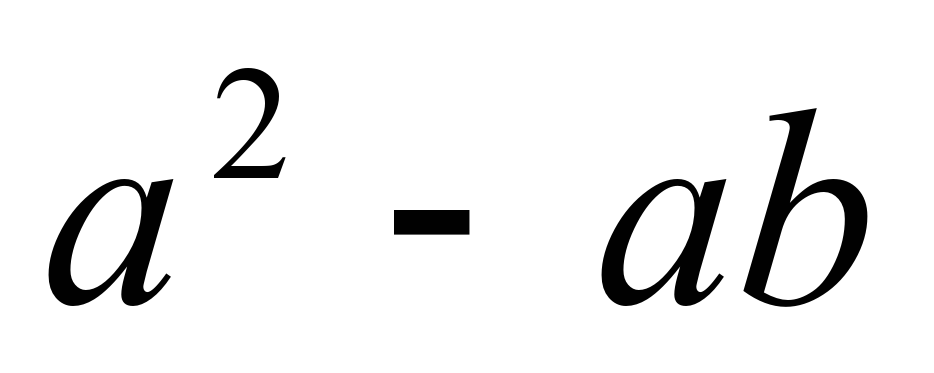 выносим тот множитель, показатель степени которой наименьший, это а. В скобках остается а минус b.
з) 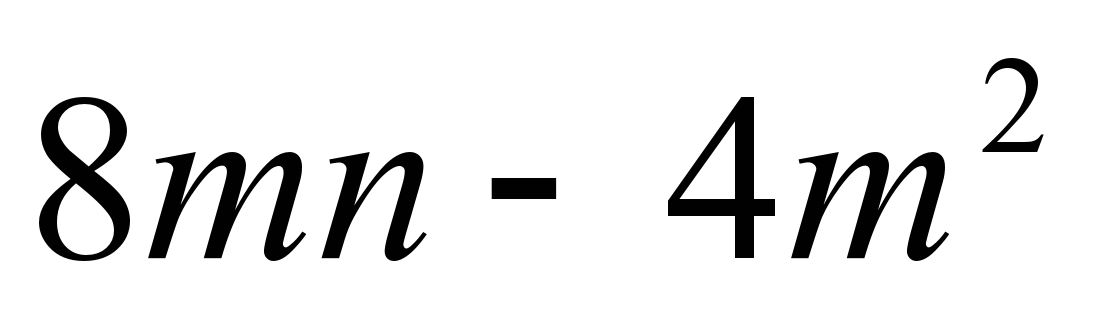 четыре
просто m 4m(2n-m)
Нужно раскрыть скобки. 4m умножить на 2n получим 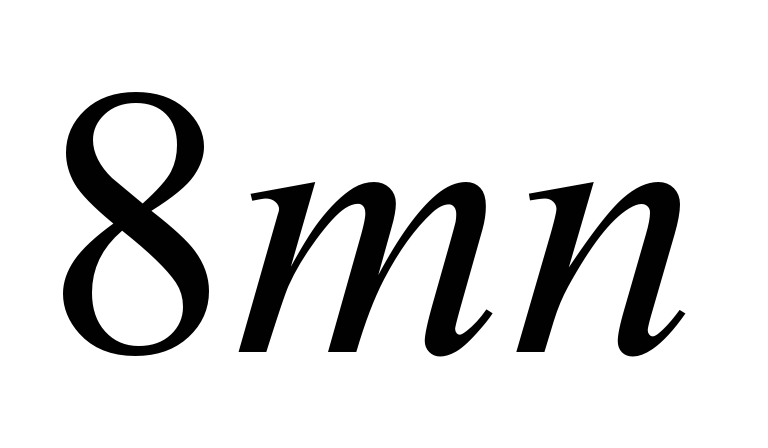 , а минус 4m умножить на m получим , а минус 4m умножить на m получим 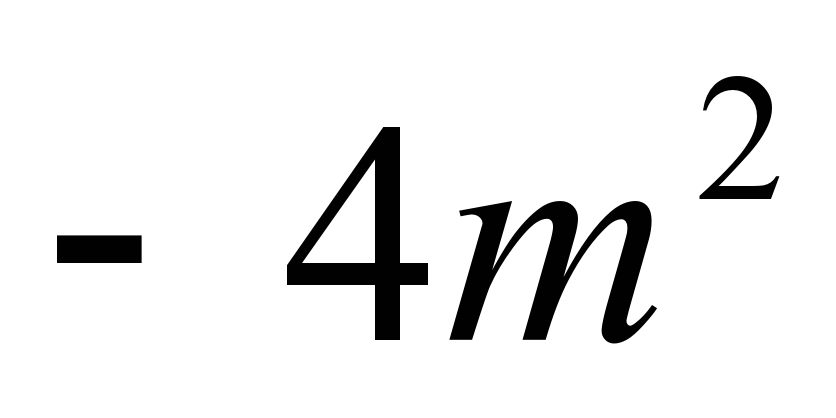 . Сходится . Сходится
Вынесите общий множитель за скобки а) 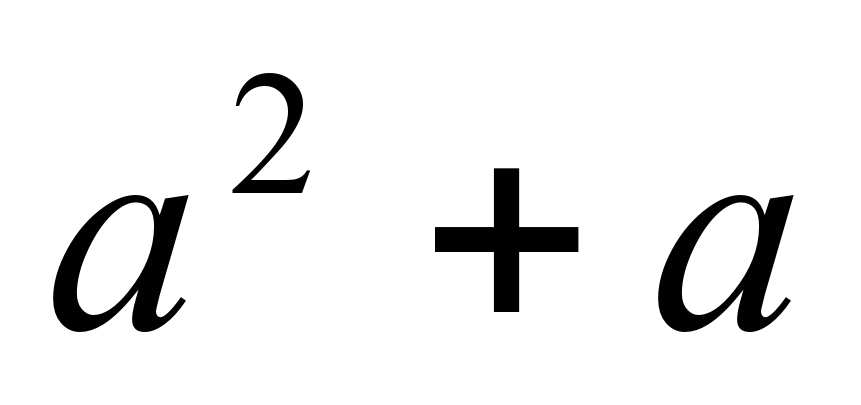 выносим тот множитель, показатель степени которой меньше, т.е. а. В скобках получается а+1.
б) 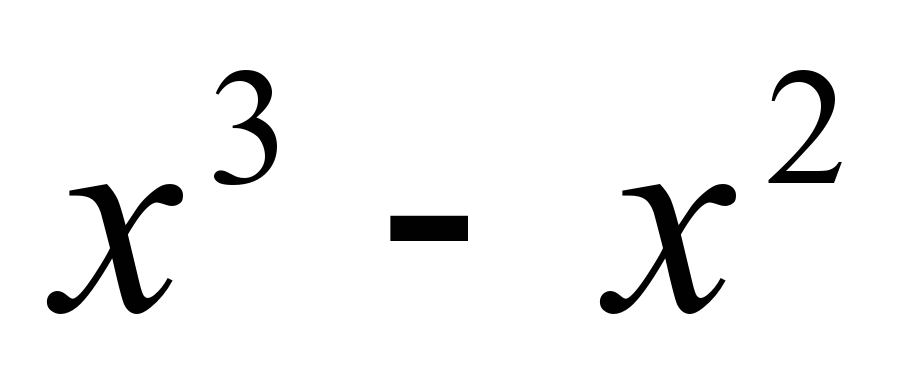 выносим тот множитель, показатель степени которой меньше, т.е. 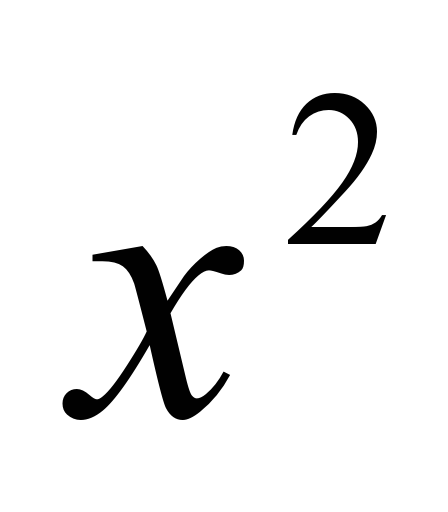 . От первого множителя остается х, от второго – единица. . От первого множителя остается х, от второго – единица. |
Справа сбоку написаны номера: № 654, № 657(1,2 ст.), № 658(1,2 ст.)
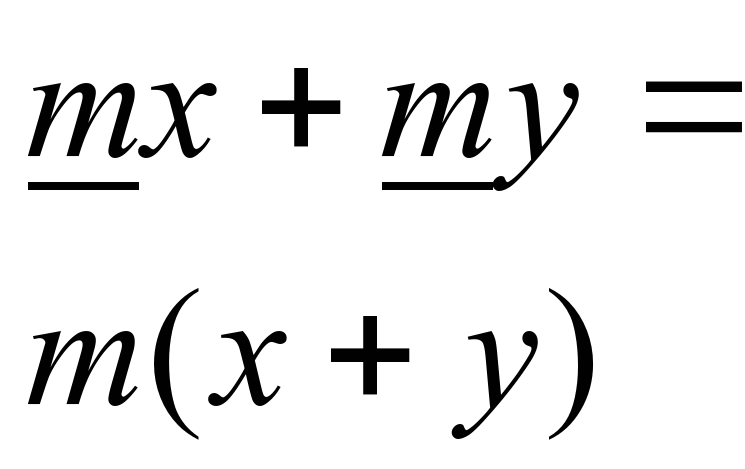
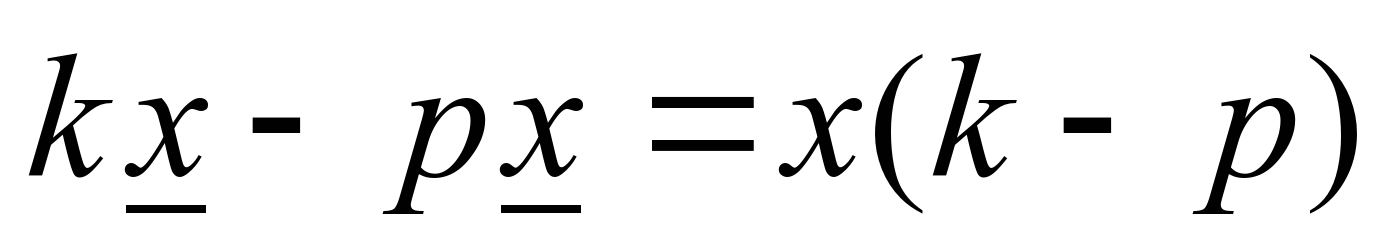
–ab+ac = -a(b+c)
–ab+ac = -a(b-c)
–ma-na = -a(m+n)
7ах+7bx = 7x(a+b)
3by-6b = 3b(y-2)
-5mn+5n = 5(–mn+n)
-5mn+5n = 5n (–m+)
-5mn+5n = 5n (–m+1)
 = 5 = 5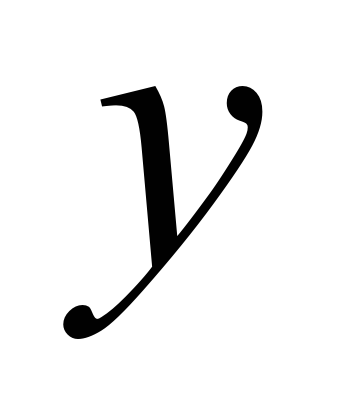 ( (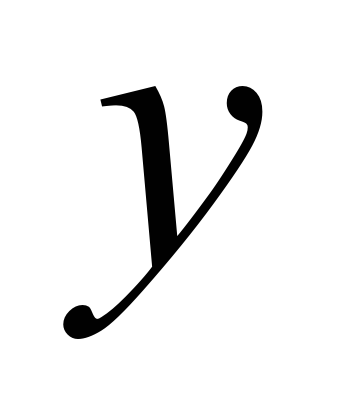 -3) -3)
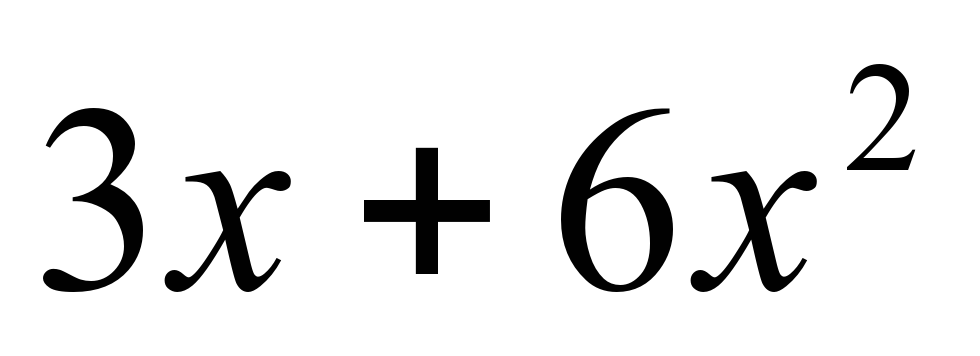 = 3х(1+2х) = 3х(1+2х)
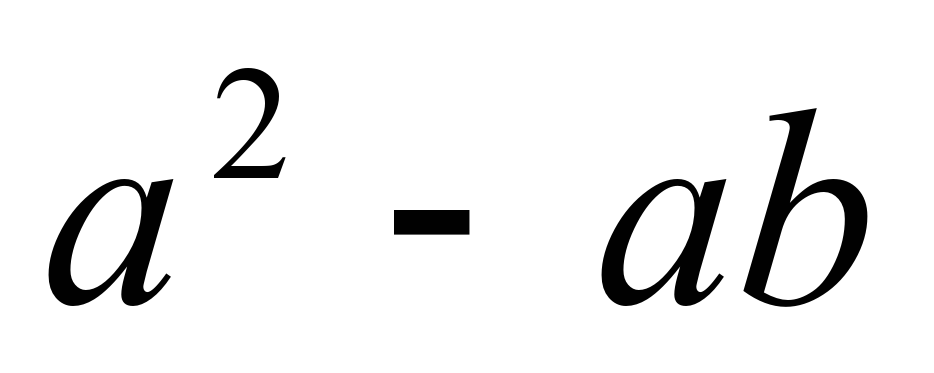 = a(a-b) = a(a-b)
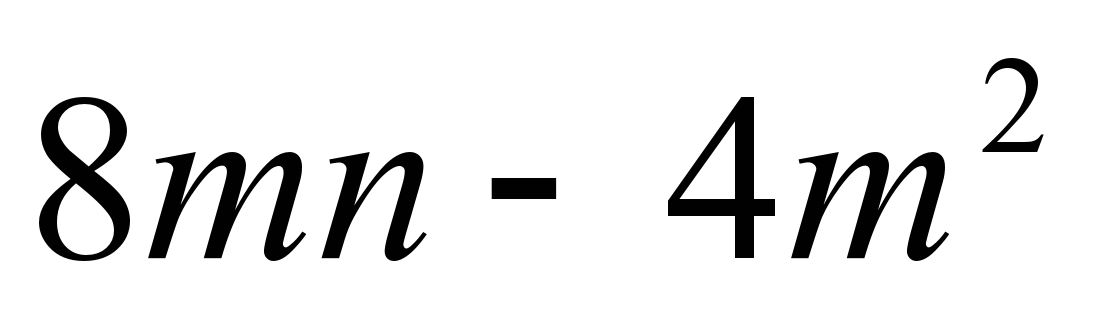 = 4m(2n-m) = 4m(2n-m)
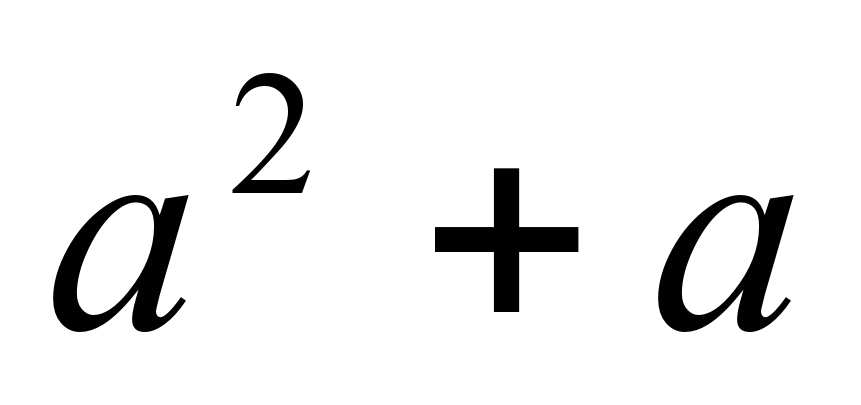 = a(a+1) = a(a+1)
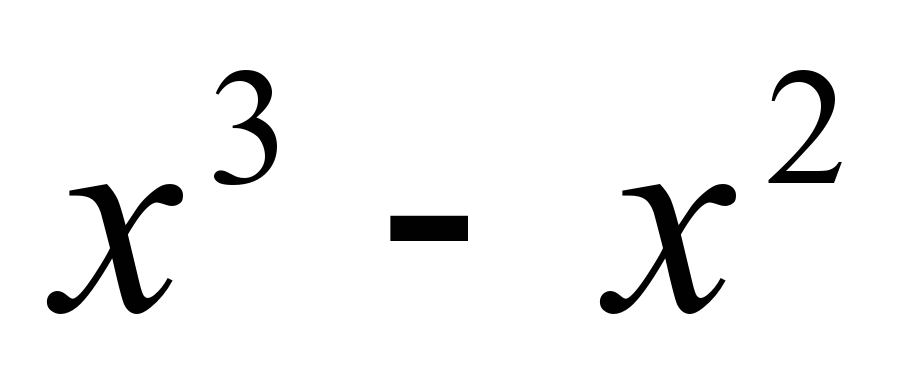 = =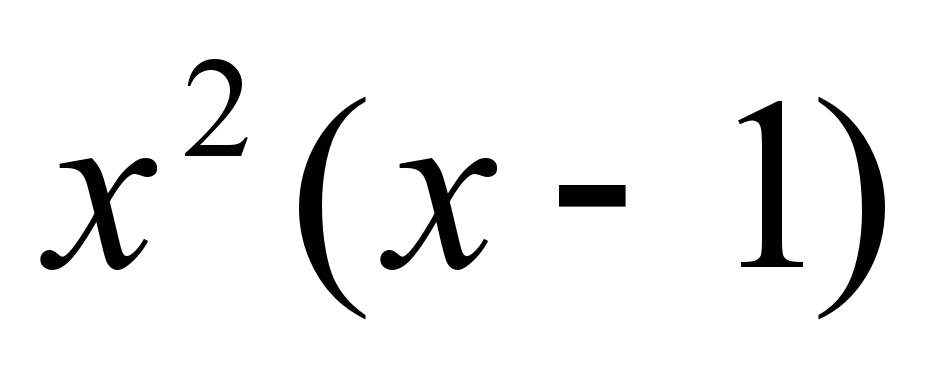
|
Постановка домашнего задания Скоро будет звонок. Открываем дневники, записываем домашнее задание: № 658 (2 столбик), № 656. Посмотрите на задание, вам нужно вынести общий множитель за скобки, чем мы с вами занимались сегодня на уроке. Отложите дневники в сторону, закройте тетради. Что сегодня нового мы узнали на уроке?
Как выносим общий множитель?
Если мы выносим весь множитель, то что от него останется? Ещё мы должны запомнить с урока одно правило, если пример состоял из двух одночленов, то и в скобках должен стоять двучлен. Если в примере было три одночлена, то и скобках при вынесении общего множителя должен быть трехчлен. Урок заканчивается со звонком. |
Тему новую проходили новую – вынесение общего множителя за скобки. Находим одинаковые множители и числовые и буквенные, их выносим, что остается записываем в скобках. Хором: единица.
| Слева на доске записано домашнее задание: Д/з № 658 (2 столбик), № 656.
|
















