| А-7. Умножение одночлена на многочлен | А-8. Определение квадратного уравнения |
| Цели урока: Образовательные применение распределительного свойства к умножению одночлена на многочлен; применение алгоритма умножения одночлена на многочлен на практике на практике.
|
формирование понятий и усвоение определений квадратного уравнения и приведенного квадратного уравнения; формирование умений находить коэффициенты квадратных уравнений. |
| Развивающие формирование приемов логического мышления, умения анализировать; развитие наблюдательности. Воспитательные |
| Оборудование: раздаточный материал, учебник, тетрадь |
| Ход урока: 1. Орг. момент (1 мин.) |
| 2. Самостоятельная работа с учебником (5 мин) Прочитать п. 27 стр. 126 | 2. Анализ контрольной работы (5 мин) Разобрать решение задания № 5 из контрольной работы |
| 3. Устная работа (10 мин) а) Верно ли утверждение, определение, свойство? Одночленом называют сумму числовых и буквенных множителей. (нет, произведение) Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена. (нет, коэффициент это числовой множитель) Одночлены, которые отличаются друг от друга только коэффициентами, называются подобными членами. (да) Алгебраическая сумма нескольких одночленов называется многочленом. (да) При умножении одночлена на одночлен получается одночлен. (да) Чтобы раскрыть скобки, перед которыми стоит знак «+», скобки надо опустить, сохранив знак каждого члена, который был заключен в скобки. (да) Чтобы раскрыть скобки, перед которыми стоит знак «-», скобки надо опустить, изменив знак каждого члена, который был заключен в скобки. (да) б) | Задание | Предполагаемый ответ | | а) - 4сх ·(-2х5) б) 0,1ху6· 10ху8 в) -15а 9 b11· (4ab) | 8сх6 х2у14 - 60а10b12 |
| 3. Актуализация опорных знаний (10 мин) Прежде чем приступить к изучению новой темы, предлагаю вспомнить известные учащимся свойства арифметического квадратного корня, решив записанные на карточке примеры. Дети не просто решат примеры, а расшифруют имя математика и астронома ІХ века, который внес существенный вклад в развитие математической науки. Каждый ответ в примере соответствует номеру буквы на другой карточке, и, записав найденные буквы, можно прочесть имя. 1. 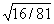 + + 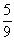 ; 2. -3 ; 2. -3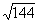 + 47; 3. 10 + 47; 3. 10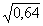 + + 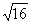 ; ; 4. 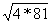 ; 5. ; 5. 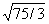 + ( + (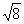 )2; 6. )2; 6. 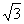 * * 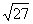 ; ; 7.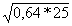 ; 8. ; 8. 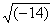 2; 9. 2; 9.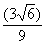 2; 10. (- 2; 10. (-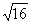 )2. )2. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | А | Д | Д | Е | К | М | Н | П | Р | | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | | Т | Л | Ь | О | З | Ф | И | Я | Х | Решение: Аль-Хорезми. |
| Физминутка (2 мин) Предлагаю детям встать, потянуться вверх, наклониться влево, вправо, выполнить вращательные движения головой. Гимнастика для глаз. |
| 4. Закрепление изученного материала (16 мин) Итак, сформулируем правило умножения одночлена на многочлен: Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Знание данной темы очень актуально. Умножение одночлена на многочлен используется при упрощении выражений, решении уравнений, задач, при решении ряда заданий ГИА.
По учебнику № 614 (а,б), 620 (а,б), 630 (а,б) | 4. Историческая справка (учащиеся знакомятся самостоятельно) (7 мин) Аль-Хорезми известен тем, что написал основополагающий трактат по алгебре. Трактат был посвящен решению уравнений и ученый рассматривал этот вопрос как самостоятельную науку. В книге Аль-Хорезми шла речь о двух важнейших операциях, необходимых при решении уравнений: переносе членов уравнения с одной стороны знака равенства в другую и о приведении подобных членов уравнения. Собственно, от названия трактата произошло слово “алгебра”. В книге содержались решения уравнений первой и второй степени таких видов: ах = b, ах2 = b, ах2 = bх, х2 + а = bх, bх + а = х2 Хорезми приводил и геометрические способы решения таких уравнений. Его книга пользовалась большой популярностью, а в математике осталось и имя автора в латинизированном виде: алгоритм. Теперь это слово обозначает всякую систему вычислений, производимых по строго определенным правилам и заведомо приводящих к решению поставленной задачи. Хорезми не высказывал мысли о своем приоритете в алгебре. Видимо, оба приема — перенос членов уравнения и приведение подобных — были уже широко известны в его время. |
|
| 5. Изучение нового материала (9 мин) (Самостоятельно) Теперь настала очередь познакомиться с тем, что такое квадратное уравнение. Используя п.21 стр. 111 учебника, ответьте на следующие вопросы: Какое уравнение называется квадратным? Придумайте и запишите несколько квадратных уравнений. Как называются числа а, в и с? Записать в тетрадь определения квадратного уравнения и приведенного квадратного уравнения. |
| Самостоятельная работа (5 мин) 1. Закончите выполнение умножения: а) 5а(3х – у) = 15ах - . . .
б) х2(х3– 4х + 2) = х5- … 2. Выполните умножение: а) 4а(х + у)
б) -3b(а + в)
в) -16у(2х – 3у + 1)
| 6. Проверка уровня усвоения теоретического материала (5 мин). Устная работа Назовите среди данных уравнения первой степени и квадратные. 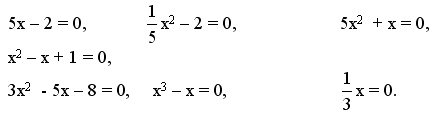
Чему равны коэффициенты уравнения? 
|
| Подведение итогов урока. Рефлексия (1 мин) |