| № этапа | Цель | Деятельность учителя | Деятельность учащегося | Время |
| I. Организационный момент. | Настроить обучащихся на продуктивную деятельность. | Организация начала урока. а) Взаимное приветствие; Сәлеметсiз бе балалар, отырыңдар! Кiм кезекше? Кiм жоқ? Я рада вас видеть! Здравствуйте ребята!
б) отметить отсутствующих;
в) проверить готовность к уроку;
г) проверка подготовленности классного помещения к уроку;
д) постановка темы, цели урока: Сегодня на уроке мы с вами обобщим и закрепим пройденный материал по теме «формулы тригонометрии», и будем применять данные формулы в решении разнообразных заданий. Эпиграфом нашего урока будут слова Блеза Паскаля: «Величие человека – в его способности мыслить».
Б. Паскаль
| Приветствуют учителя. Ответ дежурного об отсутствующих. | 3 мин. |
| II. Историческая справка. | Вовлечь и заинтересовать обучающихся историческими данными. | Пригласить учащегося к доске, для проверки домашнего задания по подготовке выступления с презентацией по историческим данным о тригонометрии. | Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников». Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц. Важный вклад в развитие тригонометрии был внесен индийской математикой в период 5- 12 век нашей эры. Индийские математики стали вычислять не полную хорду, как это делали греки, а ее половину (то есть «линию синусов»). Линия синусов именовалась ими «архаджива», буквально означало «половина тетивы лука». Индийцы составили таблицу синусов, в которой были даны значения полухорд, измеренных частями (минутами) окружности для всех углов от 0 до 90 градусов. Индийским математикам были известны соотношения, которые в современных обозначениях пишут так: sin 2 а + cos 2 а = 1; cos а = sin (90-а). В 15- 17 веках в Европе было составлено и издано несколько тригонометрических таблиц, над их составлением работали крупнейшие ученые: Н. Коперник (1540-1603); И. Кеплер (1571-1630); Ф. Виет (1540-1603). В России первые тригонометрические таблицы были изданы в 1703 году при участии Л.Ф. Магницкого. На первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Современный вид тригонометрии получила в трудах великого ученого, члена Российской академии наук Л. Эйлера (1707-1783). Эйлер стал рассматривать значения тригонометрических функций как числа - величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»). Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразное обозначение: sin а, cos а, tg а, ctg а. На основании работ Л. Эйлера были составлены учебники тригонометрии. Аналитическое (не зависящее от геометрии) построение теории тригонометрических функций, начатое Эйлером, получило завершение в трудах великого русского ученого Н.И. Лобачевского. | 3 мин. |
| Блез Паскаль (19 июня 1623—19 августа 1662) французский математик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики. Слово учителя: Когда-то Блез Паскаль сказал, что «математика – наука настолько серьёзная, что нельзя упускать случая, сделать её немного занимательной». Поэтому я предлагаю наш урок начать с занимательной странички. Угадай-ка…(ребусы)
| Угадывание ребусов (устно). 


Стихотворение (домашнее задание) Пускай кому- то мил английский,
Кому – то химия важна,
Без математики же всем нам,
Но ни туда и ни сюда. Нам уравнения, как поэмы,
И синусы поддерживают дух.
Нам косинусы, будто песни,
А формулы приведения Ласкают слух.
| 3 мин. |
| III. Актуализация опорных знаний учащихся.
| Способствовать развитию сообразительности, внимательности, активности. | 1) Повторение основных формул тригонометрии, формул сложения и двойного углов, а также решения простейших тригонометрических выражений по слайдам из презентации и в ходе следующих устных упражнений (все уравнения заранее написаны на ИД). | Устные упражнения: sin 30º = ctg 60º = cos 45º = sin 180º = cos 360º = tg 405º = sin 330º = ctg 780º =
| 2 мин. |
| 2) Ребята, давайте вспомним 6 основных тригонометрических тождеств: | sin² α + cos² α = 1 tg α · ctg α = 1 tg α = sin α ÷ cos α ctg α = cos α ÷ sin α 1 + tg² α = 1 ÷ cos² α 1 + ctg² α = 1 ÷ sin² α | 2 мин. |
| 3) Ребята, давайте вспомним формулу двойного угла синуса, косинуса, тангенса и котангенса. | cos 2α = cos² α - sin² α cos 2α = 2cos² α - 1 cos 2α = 1 - 2sin² α sin 2α = 2sin α · cos α tg 2α = (2tg α) ÷ (1 - tg² α) ctg 2α = (ctg² α - 1) ÷ (2ctg α) | 2 мин. |
| Соотнеси (индивидуально): | sin(α - β) = sin(α + β) = cos(α + β) = cos(α - β) = cos α cos β – sin α sin β sin α cos β - cos α sin β sin α cos β + cos α sin β cos α cos β + sin α sin β | 2 мин. |
| IV. Работа в парах с тестовыми заданиями.
| Способствовать развитию умения работать в паре, делиться своими знаниями с соседом по парте. | Тест. 1 вариант 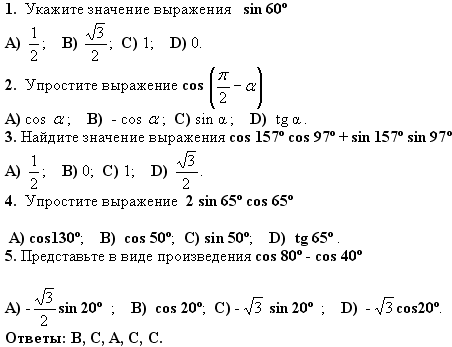
| Решение тестовых заданий, самостоятельно. Тест. 2 вариант 1. sin 5х cos 3х + sin 3х cos 5х= 1) sin 2x 2) cos x 3)sin 8x 4) cos 8x 2. cos 18ºcos 12º - sin 18ºsin 12º= 1) 1 2) -1 3) 0,5 4) √3/2 3. cos 107º cos 17º + sin 107º sin 17º = 1) 0 2) 1 3) - 1 4) 0,5 4. sin 17ºcos 13º + sin 13º cos 17º= 1) √2/2 2) 0 3) - 0,5 4) 0,5 5. cos(α + β), если α = 42º, β = 18º 1) - 0,5 2) √3/2 3) 0,5 4) -√2/2 | 4 мин. |
| V. Практические задания с применением формул тригонометрии.
| Содействовать развитию практических умений и навыков. | А сейчас ребята будем решать задания на упрощение и вычисление. Упростить: а) cos α cos 3α – sinα sin3α = б) sin 2α cos α + cos 2α sin α = в) sin α cos 3α + cos α sin 3α = Выполните взаимопроверку. | Решают у доски (2 учащихся). Вычислить: а) cos 18º cos 12º – sin18º sin12º= б) sin 40º cos 5º + cos 40º sin 5º = в) sin 10º cos 20º + cos 10º sin 20º = г) cos 7º cos 38º – sin7º sin38º = | 6 мин. |
| Физкультминутка. (физическая минутка) | Соблюдение здоровье сберегающей технологии. | Выполнение физических упражнений на разминку рук, ног, позвоночника, шеи, головы. | Выполняют упражнения, повторяя за учителем. | 3 мин. |
|
| Содействовать умению применять изученные формулы в решении примеров. | Следующее задание найди ошибку: а) sin (π-α)= sin α б) cos (3π/2+α)= - cos α в) tg (2π-α)= - tg α г) ctg (π/2+α)= ctg α Выполните самопроверку. | Решают самостоятельно и делают взаимопроверку. Сократи дробь: а) sin100º / cos50º = б) (cos 36º + sin²18º) / cos 18º = | 5 мин.
|
| VI. Самостоятельная работа: | Способствовать развитию умения самостоятельно решать задания без помощи учителя и одноклассников. | Уровень А 1. sin α·cos α·tg α = 2. 1-sin² α = Уровень B 1. (1-sin α)/cos α + tg α = 2. 1/(1+cos α)+ 1/(1-cos α) = Уровень C 1. sin α/(1+cos α)+(1+cos α)/sin α= 2. 1- sin α·cos α·ctg α= | Самостоятельно решают на скорость и правильность. | 7 мин. |
| VII. Итог урока. | Организовать завершение урока с подробным объяснением домашнего задания и комментированием оценок. | Рефлексия. Дополните фразы (на слайде )презентации. 1. сегодня я узнал…
2. было интересно…
3. было трудно…
4. я выполнял задания…
5. я понял, что…
6. теперь я могу…
7. я почувствовал, что… 8. я приобрел… 9. я научился…
10. у меня получилось … 11. я смог… 12. я попробую…
13. меня удивило…
14. урок дал мне для жизни…
15. мне захотелось… Постановка домашнего задания. №453. Объявление оценок с комментариями. Выставление оценок в дневники. Урок окончен ребята! До свидания! | Лист самоконтроля: | № задания | Количество баллов | | 1 |
| | 2 |
| | 3 |
| | 4 |
| | 5 |
| | 6 |
| | 7 |
| | Итого баллов: |
| | Оценка: |
| Учащиеся выставляют свою оценку за урок. Дополняют фразы. Записывают в дневники домашнее задание. | 3 мин. |