Конспект урока математики в 10 классе "Формулы двойного аргумента"

МБОУ гимназия №1 г. Липецка

Предмет – алгебра

Класс – 10

Учитель Попова Ольга Николаевна

Программно-методическое обеспечение:

• планирование составлено к УМК А.Г. Мордковича «Алгебра и начала математического анализа», 10 - 11 класс, М. «Мнемозина», 2013 год на основе федерального компонента государственного стандарта общего образования с учетом авторского тематического планирования учебного материала;

• Мордкович А.Г. Алгебра и начала математического анализа. 10 - 11 кл.: В двух частях. Ч. 1: Учебник для общеобразовательных учреждений (базовый уровень) / А.Г. Мордкович - М.: Мнемозина, 2013;

• Мордкович А.Г. Алгебра и начала анализа. 10 - 11 кл.: В двух частях. Ч. 2: Задачник для общеобразовательных учреждений (базовый уровень) / А.Г. Мордкович, Л.О. Денищева, Т.А. Корешкова, П.В. Семенов, Е.Е.Тульчинская - М.: Мнемозина, 2013;

• Александрова Л.А. Алгебра и начала математического анализа: самостоятельные работы. 10 класс/Л.А. Александрова. – М.: Мнемозина,2013;

• Мордкович А.Г. Алгебра и начала математического анализа. 10 - 11 классы: контрольные работы (базовыйый уровень) / А.Г. Мордкович, Е.Е. Тульчинская. – М.: Мнемозина, 2013.

Тема урока: «Формулы двойного аргумента».

Тип урока: урок изучения нового материала

Цели урока:

Образовательные: вывести формулы тригонометрии, позволяющие выражать синус, косинус и тангенс двойного угла через обычный угол, развивать умения применять их для преобразований тригонометрических выражений на уровне обязательных результатов обучения и совершенствовать вычислительные навыки.

Развивающие: развивать умения доказывать новые утверждения, наблюдать, сравнивать, анализировать и делать выводы, расширять математический и общий кругозор, используя межпредметные связи.

Воспитательные: формировать и совершенствовать такие качества личности, как трудолюбие, внимательность, любознательность, активность, умение работать четко, последовательно и аккуратно.

Оборудование: карточки для самостоятельной работы обучающего характера на уровне обязательных результатов обучения.

Ход урока

1.Организационный этап:

-приветствие;

-готовность учащихся к уроку;

-состояние рабочего места учащихся

-отсутствующие на уроке (сообщают дежурные)

Учитель. Сообщает дату и тему урока: «Формулы двойного аргумента».

2. Актуализация знаний

Устная фронтальная работа.

Озвучиваются и записываются на доске формулы синуса, косинуса, тангенса суммы и разности аргументов. Для изучения нового материала используются только формулы суммы аргументов.

sin(x +y) = sinxcosy + cosxsiny;

cos(x+y) = cosxcosy – sinxsiny;

.

3. Изучение нового материала

1.Постановка проблемного вопроса.

Как, зная формулы синуса, косинуса и тангенса суммы аргументов, получить формулы двойного аргумента (угла)?

В процессе обсуждения и поиска ответа на поставленный вопрос поступает предложение о замене различных аргументов в формулах на два одинаковых, т.е. x= y.

2.Самостоятельный вывод формул с последующей самопроверкой.

3. Трое учащихся у доски выводят новые формулы.

sin(x+y) = sinxcosy + cosxsiny
sin2x = sinxcosx + sinxcosx = 2sinxcosx

cos(x+y) = cosxcosy – sinxsiny
cos2x = cosxcox – sinxsinx = cos²x – sin²x

4.Можно ли для косинуса двойного угла получить еще две формулы, используя основное тригонометрическое тождество?

Ученики на доске записывают вывод этих формул.

cos2x = cos²x – sin²x = (1 - sin²x) - sin²x = 1 - 2 sin²x

cos2x = 1 - 2 sin²x

cos2x = cos²x – sin²x = cos²x – (1 - cos²x) = 2cos²x – 1

cos2x = 2cos²x – 1

4.Составление опорного конспекта

Составление в тетрадях опорного конспекта по теме: «Формулы двойного аргумента» (начало конспекта).

Формулы синуса и косинуса двойного аргумента справедливы для любых значений аргумента (никаких ограничений нет),тогда как формула тангенса двойного аргумента справедлива лишь для тех значений аргумента для которых определены тангенс аргумента и тангенс двойного аргумента, а также отличен от нуля знаменатель дроби.

sin2x = 2sinxcosx

cos2x = cos²x – sin²x

cos2x = 1 - 2 sin²x

cos2x = 2cos²x – 1

5. Примеры применения формул двойного угла

Все полученные формулы можно применять и в тех случаях, когда место аргумента занимает более сложное выражение. Например:

• sin10x = 2sin5xcos5x

• cos(6x – 14y) = cos²(3x – 7y) – sin²(3x – 7y)

• 

• 2sin17xcos17x = sin34x

• cos²5,5t - sin²5,5t = cos11t

Аналогичные примеры есть в учебнике. Работа с учебником: §21 стр. 122.

6. Первичное закрепление изученного материала

Задание записано на доске и выполняется по вариантам, с последующей самопроверкой. Нечетные номера для 1 варианта, а четные номера для 2 варианта. Для тех, кто работает с опережением, возможно использование заданий другого варианта.

№1. Для каждого выражения из левого столбца подберите ему тождественно равное в правом и установите соответствие.

Ответ: 1 – 2, 2 – 4, 3 – 9, 4 – 1, 5 – 7, 6 – 3, 7 – 5, 8 – 6, 9 – 8.

7. Динамическая пауза. Комплекс упражнений зарядки для глаз.

8. Самостоятельная работа по заготовленным карточкам

№2а). Найдите значения выражений:

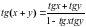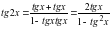
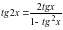
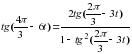
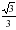Ответ: Беринговом проливе; 2 остров Ратманова; 0,75 России; 1,5 остров Крузенштерна; США; – 0,5 Тихого океана.

Дополнительная информация.

Крузенштерн Иван Федорович (1770 – 1846) – русский мореплаватель, руководил Первой русской кругосветной экспедицией (1803 – 1806гг.), одним из участников которой был М.И.Ратманов. Острова, названные в честь этих мореплавателей, входят в группу островов Диомида.

в). Выясните, какие слова не были использованы при заполнении пропусков в тексте. Составьте из них 1 – 2 предложения.

Ответ: Гринвич – район столицы Великобритании города Лондона, где находилась обсерватория, меридиан которой и был взят за основу мирового отсчета времени и долготы. Этот меридиан проходит через пролив Ла – Манш, территорию Африки и Атлантического океана (слова, которые не были использованы выделены жирным шрифтом).

9.Домашнее задание

§21, формулы, №21.10, №21.26,№21.31

10. Подведение итогов урока. Рефлексия

1). Выставление отметок за самостоятельную работу и работу у доски.

2). Ответы детей на вопросы о том, что узнали нового, что понравилось и особенно запомнилось на уроке.