модели окружности, нитка, линейка.
| Этапы урока | Деятельность учителя | Деятельность учащихся |
| 1.Организационный момент. (1 мин) 
| «Приветствие в кружок» Здравствуйте, ребята! Возьмитесь за руки, поприветствуйте друг друга. -Что мы с вами создали, взявшись за руки? -Где вы больше всего общаетесь? - Желаю вам удачного урока. Садитесь. -Сегодня будем работать в команде, и каждый ученик является участником работы, и от каждого зависит успех группы, прежде всего, и урока. Хочу познакомить с правилом работы на уроке. «Сплети веревочку» Учитель объясняет ученикам принцип самооценки своей деятельности. На каждом этапе уроке путем группового совещания вы будете прикреплять степлером на белой ленте желтое звено, если вам понравилось действие, которое вы выполняли, если нет – синее звено. Если группа не пришла к единому мнению – то зеленое звено. К концу урока у вас получится веревочка из кругов, т.е самооценок. (Оценка результата: если веревочка получилась синяя, «слабая», то урок был не понятным и не интересным, если веревочка желтая – это крепкая, надёжная цепь знаний. Зеленые прорехи говорят о несогласованности группы). Прием «Эпиграф к уроку» На доске эпиграф: «Математику нельзя изучать, наблюдая, как это делает сосед». (Айвен Нивен) - Как вы понимаете это высказывание? |
Круг или окружность. В кругу друзей
Читают
Отвечают на вопрос Если смотреть, как другие анализируют, сравнивают, преодолевают какие-то трудности, а сам ты этого ничего не делаешь, то математику знать не будешь |
| 2. Актуализация и фиксирование индивидуального затруднения в пробном действии (4 мин) 
| Устный счет Для дальнейшей работы на уроке нам нужно повторить правило округления десятичных дробей. Вспомним это правило.
Округлите 3,14159265 до десятитысячных до тысячных до сотых до десятых до целых
Решите задачу Шестиклассники решили посадить цветы: мальчики на клумбу квадратной формы, девочки – круглой формы. Решили огородить садовыми заборчиками. Сколько метров изгороди потребуется в обоих случаях?
 
2 м  2 м Как вы думаете, ребята? Как найти длину изгороди клумбы квадратной формы? Как найти длину клумбы круглой формы? - Кто нам может сказать, как вычисляется длина окружности? | Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление. Цифра, записанная в данном разряде: - не меняется, если следующая за ней справа цифра - 0, 1, 2, 3 или 4; - увеличивается на единицу, если следующая за ней справа цифра - 5,6,7,8 или 9. ≈3,1416 ≈3,142 ≈3,14 ≈3,1 ≈3
Вычислить периметр квадрата. (Обсуждение в группах и высказывание своих предположений). Нужно найти длину окружности |
| 3.Выявление места и причины затруднений 
| -Сформулируйте тему сегодняшнего урока. -Правильно. Откройте тетради, запишите число и тему урока «Длина окружности»
- Так как объектом исследования является окружность, мы должны вспомнить все про нее. ПРИЕМ «З-Х-У»
С  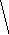
 О r А О r А d D - Какая фигура называется окружностью? Как называется точка О?
- Что такое радиус? Как обозначается радиус?
- Дайте определение диаметра. Как обозначается?
- Как связаны радиус и диаметр окружности?
| «Длина окружности».
Ребята работают в группах, потом рассказывают об окружности: столбик ЗНАЮ
и столбик ХОЧУ УЗНАТЬ |
| 4.Построение проекта выхода из затруднения (цель, тема, план, сроки, способ, средство) (2 мин) 
| Сформулируйте цели урока? - Нам предстоит решить задачу нахождения длины окружности.
- Вспомните единицы измерения длины.
- С помощью какого инструмента можно измерять длину, например, длину отрезка?
- А можно ли измерять линейкой длину окружности?
- Давайте подумаем, как можно измерять длину окружности? | Вывести формулу для вычисления длины окружности. Научиться применять эту формулу при решении задач. Ребята высказывают свое предположение
|
| 5.Реализация построенного проекта (5 мин)

| ПРИЕМ «ПРОБЛЕМНЫЙ ПОИСК» Математическое мини-исследование (в группах). На партах учеников - модели тел (цилиндров разного диаметра в основании). а) Инструктаж учителя - Давайте выполним с вами следующую практическую работу. Работать вы будете в группах. У каждой группы на столах имеются разные модели окружности, вы берете модель, обвязываете её ниткой, распрямляете и измеряете длину нитки (т.е. измерьте длину окружности.) Затем вносите результат в таблицу в столбик длина окружности, затем линейкой измеряете диаметр и вносите значение в таблицу. И потом внимательно посмотрите на последнюю колонку и сделайте вывод: во сколько раз длина окружности больше диаметра.
б) Практическая работа (учащиеся выполняют работу). | Длина окружности, С | Диаметр окружности, d | Во сколько раз длина окружности больше диаметра, С:d | ВЫВОД | |
|
|
|
|
в) Проверка работы. Учитель: - Что у вас получилось?
(Учитель выписывает несколько результатов на доске. Все они примерно одинаковы: С/d≈3,14.) г) Формулирование вывода. Учитель: Число, которое мы получили, обозначается π
π ≈ 3,1415926… д) Историческая справка. ( о числе пи)
Учитель: Число π- бесконечная десятичная дробь. Обозначение числа происходит от первой буквы греческого слова периферия, что означает "окружность". Общепринятым это обозначение стало, после издания одной из работ Эйлера.
На ранних ступенях человеческого развития пользовались неточным числом π. Оно было равно 3. Египетские и римские математики установили отношение длины окружности к диаметру не строгим геометрическим расчётом, как позднейшие математики, а нашли его просто из опыта. В 3 в. до н.э. Архимед без измерений одними рассуждениями вычислил точное значение числа π = 22/7. Далее математики вычислили 35 знаков после запятой, 707…
Такие длинные числа, приближённо выражающие значение числа π, не имеют ни практической, ни теоретической ценности. С помощью компьютера число π можно вычислить с точностью до миллиона знаков, но это представляет технический интерес, а не научный. Для обычных вычислений с числом π вполне достаточно запомнить два знака после запятой (3, 14). 26-летний мнемотехник из города Сумы Артем Гарин знает 10101 цифру после запятой в числе Пи. Он дважды упоминается в украинском Национальном реестре рекордов (это аналог Книги рекордов Гиннеса). Первый раз его туда занесли, когда Артему было 24 года. Он запомнил пять тысяч знаков после запятой числа Пи, во второй раз — когда 10101.
е) Вывод формул. Запишите формулы в тетрадь |
Учащиеся читают инструкцию к работе и выполняют самостоятельно
Выступают представители из каждой группы
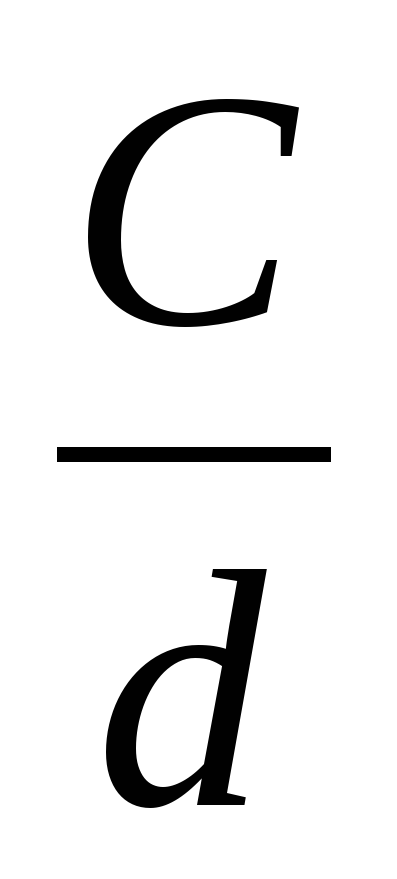
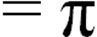 или С:d=π или С:d=π   
|
| Физкультминутка |
|
|
| 6.Первичное закрепление с проговариванием во внешней речи 
| Вернемся к нашей задаче. Вычислим длину клумбы квадратной формы. Какова же длина клумбы круглой формы? 2)Задания по группам. Решить задачи. Рассказать решение всему классу. 1 группа. Часы на белоснежной Спасской башне Кремля можно назвать главными часами Казани. Диаметр каждого циферблата - два с половиной метра, длина минутной стрелки - почти два метра. Какова длина окружности циферблата главных часов Казани? 2 группа. Радиус циферблатов Кремлевских курантов в Москве - 3,06 м, длина минутной стрелки - 3, 27 м. Какова длина окружности циферблата главных часов Москвы? Вы только представьте: в окружность циферблата столичных курантов может заехать вагон поезда, в окружность циферблата главных часов Казани - «ГАЗель»... 3 группа. Длина окружности цирковой арены составляет 40,82 м. Найдите диаметр арены цирка. Диаметр арены во всех цирках мира одинаковый и составляет ровно 13 метров (42 фута).Такой диаметр был и по сей день остается профессиональной необходимостью: дело в том, что только по такому кругу лошадь может бежать галопом с определенной скоростью так, чтобы ее спина всегда оставалась под одним углом к центру арены. Это необходимо для выполнения акробатических номеров на лошадях – ведь современный цирк начинался именно с них. 4 группа. Правый берег Казанки украшает новый дворец бракосочетания под названием «Казан» или «Чаша». Длина окружности верхней цилиндрической части примерно 131,88 метра. Найдите радиус окружности цилиндрической части «Чаши». Открытие достопримечательности произошло летом 2013 года. Изюминкой здания стала смотровая площадка Чаши, расположенная на высоте 32 метра. А также форма самого дворца, которая похожа на большую чашу или казан, отсюда соответственно и название здания. -Что объединяет все эти задачи? -Правильно. Поднимите руки, кто побывал в Казани. Я уверена, вы согласитесь, если я скажу, что Казань – удивительно красивый город. После Москвы и Санкт-Петербурга столицу нашей республики считают третьей столицей России по значимости и красоте ее архитектурных и исторических памятников. Ее визитной карточкой являются Кремль и площадь Тысячелетия. |
Р= 2*4=8 (м) С= π* 2=3,14*2=6,28 (м)
С=πd С=3,14*2,5=7,85 (м)
C=2πr С=2*3,14*3,06=19,2168≈19,22 (м)
d=C: π d=40,82:3,14=13(м)
r=C : (2π) r=131,88 : (2*3,14)=21(м)
Говорится о достопримечательностях Казани |
| 7.Самостоятельная работа с самопроверкой по эталону 
| ТЕСТ - 1 вариант | № | ВОПРОС | ОТВЕТ | | 1 | Отрезок, соединяющий две точки окружности и проходящий через ее центр | А) сторона, Б) диаметр, В) радиус | | 2 | Число π приближенно равно | А) 3, 15 Б)3,14 В)6,28 | | 3 | Формула для вычисления длины окружности | А) С=πr Б) С=πd В) C=2πd Г) C=2r | | 4 | Чему равен диаметр окружности, радиус которой 3,2 см? | А) 1,9 Б) 6,6 В) 7,6 Г) 6,4 | | 5 | Колесо преодолело расстояние 17,5 м за семь оборотов. Длина окружности колеса | А) 2,5 м Б) 0,25 м В) 25 м Г)122,5 м | ТЕСТ - 2 вариант | № | ВОПРОС | ОТВЕТ | | 1. | Отрезок, соединяющий центр окружности с точкой на окружности | А) хорда, Б) диаметр, В) радиус | | 2. | Чему равен диаметр окружности, если её радиус 4,7 м? | А) 8,14 Б) 2,35 В) 9,4 | | 3. | Число π приближённо равно | А) 3, 15 Б)3,14 В)6,28 | | 4. | Формула для вычисления длины окружности | А) C = 2 πd Б) C = 2 πr В) C = πr Г) C = 2d | | 5. | Колесо преодолело расстояние 17,5 м за пять оборотов. Длина окружности колеса | А) 87,5 м Б) 3,5 м В) 0,35 м Г) 35 м | Проверка ответов 1 вариант | № | ВОПРОС | ОТВЕТ | | 1 | Отрезок, соединяющий две точки окружности и проходящий через ее центр | Б) диаметр | | 2 | Число π приближенно равно | Б)3,14 | | 3 | Формула для вычисления длины окружности | Б) С=πd
| | 4 | Чему равен диаметр окружности, радиус которой 3,2 см? | Г) 6,4 | | 5 | Колесо преодолело расстояние 17,5 м за семь оборотов. Длина окружности колеса | А) 2,5 м
| 2 вариант | № | ВОПРОС | ОТВЕТ | | 1. | Отрезок, соединяющий центр окружности с точкой на окружности | В) радиус | | 2. | Чему равен диаметр окружности, если её радиус 4,7 м? | В) 9,4 | | 3. | Число π приближённо равно | Б)3,14 | | 4. | Формула для вычисления длины окружности | Б) C = 2 πr | | 5. | Колесо преодолело расстояние 17,5 м за пять оборотов. Длина окружности колеса | Б) 3,5 м | – Кто выполнил все задания теста правильно? Поднимите руки. – Молодцы! – А кто допустил одну ошибку? (Выставляются баллы). | Индивидуально на листочках с последующей взаимопроверкой. Учащиеся выполняют тест, помечая правильный ответ, затем обмениваются работами с соседом по парте. При этом открываются правильные ответы и выставляются баллы по количеству правильных ответов |
| 8.Включение в систему знаний и повторение 
| -А теперь возьмите листы с таблицей и заполните третий столбик УЗНАЛ - Ребята, а как вы думаете, со всеми ли характеристиками, связанными с окружностью мы познакомились? -Какую величину, связанную с окружностью или кругом, можно еще найти? - А вывести формулу площади круга вам предстоит на следующем уроке. |
Заканчивают таблицу «ЗХУ», озвучивают результаты своей деятельности -Вывели формулы для вычисления длины окружности… -Применяли эти формулы для решения задач
Это площадь круга |
| 9.Рефлексия учебной деятельности на уроке 
| 1. Итоги урока – Мы на славу потрудились. Пришло время подвести итоги нашего исследования. - Я предлагаю каждой группе продемонстрировать свою сплетенную веревочку и высказать мнение о том, что им понравилось, что было интересно, непонятно, нужны ли новые знания в дальнейшей жизни. В каждой группе каждый член высказывает свое одно предложение, либо мысль 2. Разноуровневое домашнее задание 1) №867, 868 2) Творческое задание. Придумайте и составьте задачу по теме «Длина окружности» и сделайте красочный рисунок к задаче. 3. Выставление оценок. (Отметить учеников, активно работавших на уроке) |
Каждая группа отмечает наиболее отличившегося и внесшего больший вклад в решение задач ученика.
Выбирают домашнее задание
Выставляют оценки за урок |







 О r А
О r А





















